Dada una ecuación de recta del tipo y mx n + , la interpretación de
Anuncio
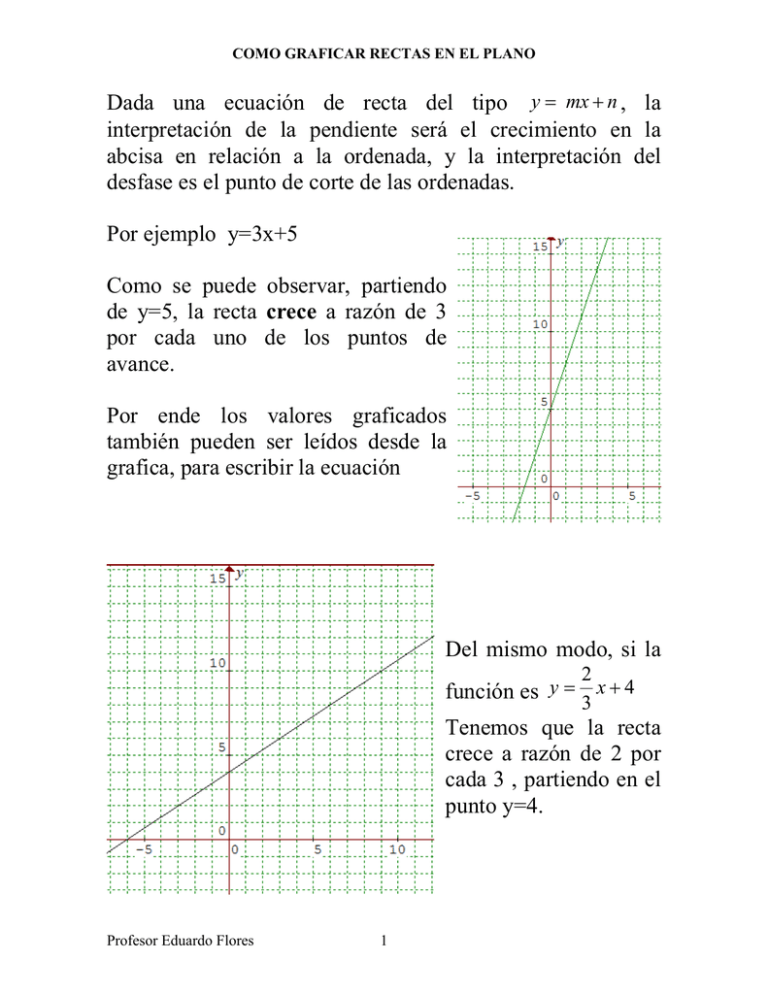
COMO GRAFICAR RECTAS EN EL PLANO Dada una ecuación de recta del tipo y = mx + n , la interpretación de la pendiente será el crecimiento en la abcisa en relación a la ordenada, y la interpretación del desfase es el punto de corte de las ordenadas. Por ejemplo y=3x+5 Como se puede observar, partiendo de y=5, la recta crece a razón de 3 por cada uno de los puntos de avance. Por ende los valores graficados también pueden ser leídos desde la grafica, para escribir la ecuación Del mismo modo, si la función es y = 2 x+4 3 Tenemos que la recta crece a razón de 2 por cada 3 , partiendo en el punto y=4. Profesor Eduardo Flores 1 COMO GRAFICAR RECTAS EN EL PLANO Ejercicio. Identifique que recta corresponde a cual ecuación y = 3x + 4 y = -x + 5 y = 2x - 3 y = -2 x - 4 y = x+2 2 x+4 3 y = 3x - 5 y= y= y= -1 x +1 3 3 x+5 4 Cuando la ecuación esta dada de la forma ax + by + c = 0 , es decir en su forma general, bastara con despejar cada componente como independiente. Ejemplo 2 x + 3 y = 12 Despejando cada variable tenemos que x = 6 e y = 4 , por consecuencia Profesor Eduardo Flores 2 y= 3 x-2 4 y= 2 x-2 3 COMO GRAFICAR RECTAS EN EL PLANO Al unir los puntos la gráfica es explicita para su análisis Lo cual implica que la ecuación pertinente al modelo −4 anterior quedara que la ecuación particular será y = 6 x + 4 Lo cual deberá ser convenientemente simplificado a la forma y= −2 x+4 3 Profesor Eduardo Flores 3 COMO GRAFICAR RECTAS EN EL PLANO Ejercicio: Dadas las ecuaciones pertinentes a las siguientes rectas graficarlas en el plano cartesiano mostrado 2 x + 3 y = 24 3x − 2 y = 12 −3x + 5 y = 30 −2 x + 4 y = 20 −3x + 4 y = −24 2 x − 5 y = 20 Profesor Eduardo Flores 4 www.crisol.tk COMO GRAFICAR RECTAS EN EL PLANO Solución 2 x + 3 y = 24 3x − 2 y = 12 −3x + 5 y = 30 −2 x + 4 y = 20 −3x + 4 y = −24 2 x − 5 y = 20 Profesor Eduardo Flores 5 www.crisol.tk COMO GRAFICAR RECTAS EN EL PLANO Ejercicio. Dadas las siguientes rectas determine la ecuación pertinente a cada una Indique su forma general, su forma particular, y estime las coordenadas del punto de intersección. Profesor Eduardo Flores 6 www.crisol.tk






