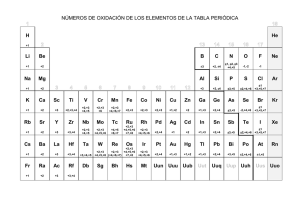
UNIDAD V. OXIDO REDUCCION

REPUBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD EXPERIMENTAL SUR DEL LAGO “Jesús María Semprúm”
PROGRAMA DE INGENIERÌA EN ALIMENTOS.
UNIDAD CURRICULAR: QUIMICA INORGANICA.
UNIDAD V. OXIDO-REDUCCION.
Prof. David Mejias
2011
UNIDAD V. OXIDO REDUCCION.
DEFINICIONES.
La oxidación se define como la perdida de electrones y la reducción como la ganancia de
electrones por un átomo dado. También puede definirse como el aumento en el estado de
oxidación, mientras que la reducción se define como la disminución del estado de
oxidación. En una oxido-reducción, la oxidación y la reducción ocurren simultáneamente;
dependiendo una de la otra, y el numero de electrones perdidos por una especie en la
oxidación debe ser igual al numero de electrones ganados por la otra especie en la
reducción. Por ejemplo:
2Fe0 + 3Cl20 → 2Fe+3Cl3-1
Como se ve no hay exceso ni deficiencia de electrones, aunque las especies químicas
participantes han cambiado sus estados de oxidación, la carga neta sigue siendo igual a
ambos lados de la reacción, es decir, igual a cero (0).
También podemos ver que el Fe paso de 0 a +3, es decir, se oxido, mientras que el Cl
paso de 0 a -1, es decir, se redujo.
UNIDAD V. OXIDO REDUCCION.
DEFINICIONES.
Se puede decir, que el agente oxidante es el Cl y el agente reductor es el Fe. En una
reacción redox, como suele llamarse a las reacciones de oxido-reducción, el agente
oxidante es el que recibe los electrones y el agente reductor el que los suministra. Para
entender mejor todo esto podemos separar la ecuación anterior en sus dos
semireacciones:
Fe0 → Fe+3 + 3e- (Oxidación, entonces el Fe es el reductor)
3Cl0 + 3e- = 3Cl-
(Reducción, entonces el Cl es el oxidante)
NUMEROS DE OXIDACION.
Este tipo especial de valencia, que toma en consideración la polaridad de los enlaces
covalentes que ocurre entre los átomos, se denomina número de oxidación, conocido
también como estado de oxidación o estado de valencia.
El número de oxidación es un concepto útil para conocer el estado de oxidación o
reducción de átomos particulares en compuestos como K2Cr2O7, KMnO4 y Cu(NO3)2 entre
otros.
UNIDAD V. OXIDO REDUCCION.
DEFINICIONES.
El estado de oxidación de un átomo en una combinación química determinada es la carga
eléctrica arbitraria asignada a dicho átomo según una serie de reglas prescritas que se
establecen a continuación:
1.- El número de oxidación de cualquier elemento libre es cero; así, H2, O2, Fe, Cl2 y K
tienen número de oxidación cero.
2.- El número de oxidación de cualquier ión monoatómico es igual a su carga; así, Na+
tiene número de oxidación +1, Ca+2 de +2 y Cl- de -1.
3.- El número de oxidación del H en todos los compuestos no iónicos es +1. Por ejemplo
H2O, NH3, HCl y CH4. Pero para los hidruros metálicos iónicos como NaH, el número de
oxidación del hidrógeno es -1.
4.- El número de oxidación del oxígeno es -2 en todos los compuestos en que no forme el
enlace covalente O-O (peróxido). Por ejemplo en el H2O, H2SO4, CO2, HNO3 y NO. Pero
en el peróxido de hidrógeno, H2O2, el número de oxidación del oxígeno es -1. Otra
excepción a la regla es OF2, donde el oxígeno tiene número de oxidación +2 y F es -1.
UNIDAD V. OXIDO REDUCCION.
CONTINUACION.
5.- En las combinaciones entre los no metales en las que no intervenga el hidrógeno o el
oxígeno, el no metal que está por encima o la derecha del otro en la tabla periódica se
considera negativo. Por ejemplo, en BrF3, el número de oxidación del fluor es -1 y el del
bromo es de +3; mientras que en el AsBr3 el bromo es -1 y el arsénico es +3.
6.- La suma algebraica de los números de oxidación de todos los átomos de una fórmula
para un compuesto neutro debe ser cero. Por tanto, en el HNO3, como el número de
oxidación total de los tres oxígenos es 3(-2) = -6, y el número de oxidación del hidrógeno
es +1, el del nitrógeno debe ser +5, a fin de que la suma +1 +5 -6 = 0.
7.- La suma algebraica de los números de oxidación de los átomos de un ión, debe ser
igual a la carga del ión. Así, en el NH4+, el número de oxidación del nitrógeno debe ser -3,
que -3 + 4 = +1. En el SO3-2, el número de oxidación del S debe ser +4, ya que +4 -6 = -2.
HAGAMOS UNOS EJERCICIOS:
UNIDAD V. OXIDO REDUCCION.
EJERCICIOS DE NUMERO DE OXIDACION.
1.- Verificar los números de oxidación del N en la siguiente lista:
NO2, NO3-, N2O, N2O3, N2O5.
2.- Verificar los números de oxidación del Cl en la siguiente lista:
ClO4-, ClO3-, ClO2-, ClO-
BALANCEO DE LAS ECUACIONES DE OXIDO REDUCCION.
Las reacciones de oxido-reducción pueden ocurrir con sustancias puras o con especies en
solución. En el primer caso se escribe la ecuación total; en el segundo caso se escribe la
ecuación iónica neta. Sin embargo, la predicción de los productos no es una tarea fácil y
requiere de mucha experiencia. Además, las reacciones redox en soluciones acuosas son
algo complicadas por que el solvente (H2O) y otras partículas como H+ (en solución ácida)
y OH- (en solución básica) pueden tomar parte en las reacciones. Por lo tanto, siempre
indicaremos cuales son los productos que toman parte de la reacción y las condiciones de
la solución, es decir, si es ácida o básica.
UNIDAD V. OXIDO REDUCCION.
BALANCEO DE LAS ECUACIONES DE OXIDO REDUCCION.
Para balancear una reacción de óxido-reducción, generalmente se usan dos métodos, el
método del ión-electrón y el método del cambio en el número de oxidación.
METODO ION-ELECTRON.
1.- Escribir una ecuación que incluya a los reactivos y productos que contengan a los
elementos que hayan sufrido cambios en su estado de oxidación.
2.- Escribir una ecuación parcial para el agente oxidante y otra para el agente reductor.
3.- Igualar cada ecuación parcial en cuanto al número de átomos de cada elemento. En
soluciones ácidas o neutras puede añadirse H2O e H+ para balancear los átomos de
oxígeno e hidrógeno. Por cada átomo de oxígeno en exceso en un lado de la ecuación se
iguala agregando H2O en el otro lado. Si la solución es alcalina, puede utilizarse OH-. Por
cada oxígeno en exceso en un lado de la ecuación se iguala añadiendo H2O en el mismo
lado y OH- en el lado contrario.
4.- Igualar cada ecuación parcial en cuanto al número de cargas añadiendo electrones en
el primero o segundo miembro de la ecuación.
5.- Multiplicar cada ecuación por los mínimos coeficientes para igualar la pérdida y
ganancia de electrones.
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
6.- Sumar las dos ecuaciones parciales que resultan de estas multiplicaciones. En la
ecuación resultante anular todos los términos semejantes a ambos lados de la ecuación.
Todos los electrones deben anularse.
7.- Simplificar los coeficientes.
VEAMOS UN EJEMPLO.
A.- Balancear la siguiente ecuación iónica por el método del ión-electrón:
Cr2O7-2 + Fe+2 → Cr+3 + Fe+3.
Paso 1. Hacer las ecuaciones parciales.
Semirreacción (1a)
Cr2O7-2 → Cr+3
(Reducción)
Semirreacción (2a)
Fe+2 → Fe+3
(Oxidación)
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
Paso 2. La semireacción (1a) requiere de 7 H2O a la derecha, para igualar los 7 Oxígenos
de la izquierda, luego se colocan 14 H+ a la izquierda para igualar los 14 H de la derecha,
también se igualan los Cr, colocando un 2 del lado derecho. La 1b no necesita balanceo,
porque está balanceada. Así, tenemos las semireacciones:
Semirreacción (2a)
Cr2O7-2 + 14H+ → 2Cr+3 + 7H2O
Semirreacción (2b)
Fe+2 → Fe+3
Paso 3. Se efectúa el balanceo de cargas. En la ecuación 2a, la carga neta en el lado
izquierdo es de +12 y en el lado derecho de +6, por lo que añadimos 6e-, en lado izquierdo.
En la ecuación 2b, se suma 1e- en el lado derecho, para que quede una carga de +2 en el
lado derecho:
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
Así, tenemos las semireacciones: 3a y 3b
Semirreacción (3a) Cr2O7-2 + 14H+ + 6e- → 2Cr+3 + 7H2O
Semirreacción (3b)
Paso 4. Se igualan los electrones ganados y perdidos. Basta con multiplicar la ecuación 3b
por 6 y la ecuacion 3a por 1. Así, tenemos las semirreacciones 4a y 4b.
Semirreacción (4a) Cr2O7-2 + 14H+ + 6e- → 2Cr+3 + 7H2O
Semirreacción (4b)
Fe+2 →
Fe+3 + 1e-
6Fe+2 → 6Fe+3 + 6e-
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
Paso 5. Se suman las semirreacciones 4a y 4b y se simplifican los electrones. Así,
tenemos la ecuación balanceada
Semirreacción (4a) Cr2O7-2 + 14H+ + 6e- → 2Cr+3 + 7H2O
Semirreacción (4b)
+
6Fe+2 → 6Fe+3 + 6e-
Cr2O7-2 + 14H+ + 6e- + 6Fe+2 → 2Cr+3 + 7H2O + 6Fe+3 + 6eCr2O7-2 + 14H+ + 6Fe+2 → 2Cr+3 + 7H2O + 6Fe+3
VEAMOS OTRO EJEMPLO:
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
Balancear la ecuación I- + H2O2 → I2(acuoso) + H2O (en solución ácida).
Paso 1. Escribimos las semirreacciones donde hay cambios en el estado de oxidación y
así, tenemos:
Semirreacción (1a)
Semirreacción (1b)
Paso 2. Se balancea la semirreacción 1a, colocando 2 del lado izquierdo. En la
semirreacción 2a se coloca una H2O, para igualar el número de oxígenos, al mismo tiempo
se colocan 2 H+, al lado izquierdo para balancear los hidrógenos y así quedan las
semirreacciones:
Semirreacción (2a)
2I- → I2
Semirreacción (2b)
H2O2 + 2H+ → H2O + H2O
I- → I2
(Oxidación)
H2O2 → H2O (Reducción)
UNIDAD V. OXIDO REDUCCION.
METODO ION-ELECTRON.
Paso 3. Se balancea las cargas eléctricas. En 2a, se colocan 2 electrones del lado
derecho, para balancear las 2 cargas negativas de la izquierda. En la semirreacción 2b se
coloca un par de electrones del lado izquierdo para balancear las dos cargas positivas de
los 2H+ y así, quedan las semirreacciones:
Semirreacción (3a)
Semirreacción (3b)
Paso 4. Se suman las dos semirreacciones y se simplifican los electrones.
2I- → I2 + 2eH2O2 + 2H+ + 2e- → 2H2O
2I- → I2 + 2eH2O2 + 2H+ + 2e- → 2H2O
2I- + H2O2 + 2H+ + 2e- → I2 + 2e- + 2H2O
Paso 5. Se simplifican los términos comunes.
2I- + H2O2 + 2H+ → I2 + 2H2O
UNIDAD V. OXIDO REDUCCION.
METODO DEL CAMBIO EN EL NUMERO DE OXIDACIÓN.
Paso 1. Escribir una ecuación que represente la reacción. Es necesario conocer los
reactivos y productos que contienen los elementos que sufren cambios en su número de
oxidación.
Paso 2. Determinar la variación que sufre en su estado de oxidación un elemento del
agente oxidante y un elemento del agente reductor.
Paso 3. Ajustar los coeficientes en ambas ecuaciones electrónicas, teniendo en cuenta que
el número de electrones perdidos sea igual al número de electrones ganados.
Paso 4. Completar por simple inspección los coeficientes apropiados para el resto de la
ecuación de modo que satisfaga la igualdad de los átomos.
VEAMOS UN EJEMPLO:
Balancear la siguiente ecuación de óxido-reducción: Fe+2 + MnO4- → Fe+3 + Mn+2 en
solución ácida.
UNIDAD V. OXIDO REDUCCION.
METODO DEL CAMBIO EN EL NUMERO DE OXIDACIÓN.
Paso 1. Se identifica el elemento oxidado y el elemento reducido.
Fe+2 → Fe+3
MnO4- → Mn+2
Paso 2. Se determina la variación que sufre en su estado de oxidación un elemento
oxidante y un elemento reductor.
Fe+2 → Fe+3 + 1e- (Aumento de 1)
MnO4- + 5e- → Mn+2
(Disminución de 5)
Paso 3. Se ajustan los coeficientes en ambas ecuaciones electrónicas, para este caso se
multiplica la primera ecuación por 5 y la segunda por 1:
5 x ( Fe+2 → Fe+3 + 1e-) = 5Fe+2 → 5Fe+3 + 5e1 x (MnO4- + 5e- → Mn+2) = MnO4- + 5e- → Mn+2
Paso 4. Se suman las ecuaciones y se simplifican los términos semejantes, luego se
completan los coeficientes apropiadamente.
UNIDAD V. OXIDO REDUCCION.
METODO DEL CAMBIO EN EL NUMERO DE OXIDACIÓN.
5 x ( Fe+2 → Fe+3 + 1e-) = 5Fe+2 → 5Fe+3 + 5e1 x (MnO4- + 5e- → Mn+2) = MnO4- + 5e- → Mn+2
5Fe+2 + MnO4- + 5e- → 5Fe+3 + 5e- + Mn+2
5Fe+2 + MnO4- → 5Fe+3 + Mn+2
Paso 5. Se ajustan las cargas en cada lado de la ecuación, tomando en cuenta que la
reacción es en medio ácido. Según la ecuación anterior la carga en el lado izquierdo es de
(5 x 2) – 1 = +9, mientras que en el lado derecho tenemos (5 x 3) + 2 = +17. Si añadimos
8H+ al lado izquierdo y 1/2 H2O por cada H+, tenemos:
5Fe+2 + MnO4- + 8H+ → 5Fe+3 + Mn+2 + 4H2O
UNIDAD V. OXIDO REDUCCION.
REPRESENTACION DE PILAS GALVANICAS Y ELECTROLITICAS.
Ya se definió la oxidación como el aumento en el estado de oxidación de los átomos o
iones y la reducción como la disminución en el estado de oxidación de dichas partículas.
Por ejemplo cuando el cloro y el sodio reaccionan se produce cloruro de sodio, compuesto
formado por iones Na+ y Cl-. Esta es una reacción de óxido-reducción.
Oxidación: 2Na = 2Na+ + 2e-
Reducción: Cl2 + 2e- = 2Cl-
2Na + Cl2 → 2NaCl
En este ejemplo la pérdida de 2e- por parte de los 2Na, hace que cada uno de éstos
aumente su numero de oxidación de 0 a +1, oxidándose entonces. Simultáneamente la
ganancia de 2e-, por parte del Cl2, hace que cada cloro disminuya su número de oxidación
de 0 a -1, reduciéndose en consecuencia.
UNIDAD V. OXIDO REDUCCION.
REPRESENTACION DE PILAS GALVANICAS Y ELECTROLITICAS.
Existe un tipo de reacciones que se denominan: reacciones electroquímicas, que son en esencia
reacciones de óxido-reducción, en las cuales los electrones que se ganan y se pierden por las especies
reaccionantes, se mueven a través de un material conductor.
Por conveniencia el campo de la electroquímica puede dividirse en dos grandes secciones; una se
refiere a las reacciones químicas que producen una corriente eléctrica y que se llevan a cabo en una
celda o pila galvánica y la otra se refiere a las reacciones químicas que se producen mediante una
corriente eléctrica, en un tipo de proceso que se denomina electrólisis.
PILAS GALVANICAS.
En 1786, el profesor de anatomía de la Universidad de Bolonia, Luigi Galvani, notó que los músculos de
las ancas de rana convulsionaban cuando les llegaba una descarga eléctrica. También se dio cuenta
que estos músculos se contraían y relajaban cuando se ponían en contacto con dos metales distintos,
de allí surgió la pregunta: la electricidad que causa estas convulsiones ¿es debida a los metales o al
músculo? A pesar de que Galvani erró en su respuesta, su nombre pasó a la historia y la electricidad
producida por dos metales en contacto se llama electricidad galvánica en su honor; el hierro que se
cubre con cristales de cinc por medio de corriente eléctrica se llama hierro galvanizado y el aparato
que detecta el paso de corriente eléctrica se llama galvanómetro.
UNIDAD V. OXIDO REDUCCION.
PILAS GALVANICAS.
Un aspecto muy importante de las reacciones de óxido-reducción es que se pueden llevar
a cabo estando los reaccionantes separados por un espacio y unidos solamente por una
conexión eléctrica. La siguiente figura es una ilustración de una celda galvánica:
UNIDAD V. OXIDO REDUCCION.
PILAS GALVANICAS.
La imagen anterior ilustra una reacción entre el Zn metálico y el ión cúprico:
Zn(s) + Cu+2(acuoso) → Cu(s) + Zn(acuoso)
Los electrones fluyen desde la placa de Zn (ánodo), a lo largo del circuito externo con
producción simultánea de iones Zn+2, mientras la placa de Zn se disuelve. Este proceso se
puede resumir escribiendo:
Zn = Zn+2 + 2eTambién se observa que los electrones fluyen hacia la placa de Cu (cátodo), mientras los
iones cúpricos dejan la solución para depositarse en forma de cobre metálico, lo que se
puede representar por la siguiente ecuación:
Cu+2 + 2e- = Cu
UNIDAD V. OXIDO REDUCCION.
PILAS GALVANICAS.
El propósito del puente salino es evitar toda acumulación de carga neta en cualquiera de los
vasos, permitiendo a los iones negativos difundir desde el vaso de la derecha por el puente
salino hacia el vaso de la izquierda. Al mismo tiempo puede haber difusión de iones positivos
desde la izquierda hacia la derecha.
POTENCIAL ESTANDAR Y COMBINACION DE PARES.
El funcionamiento de la celda galvánica descrita anteriormente sugiere que la reacción completa
de óxido-reducción se puede separar en dos semirreacciones como sigue:
Zn = Zn+2 + 2e-
Cu+2 + 2e- = Cu______
Cu+2 + Zn = Zn+2 + Cu
La celda completa produce un flujo de electrones en el circuito exterior. En la media celda, del
agente reductor (Zn en este caso), el producto de oxidación se acumula durante el
funcionamiento de la celda.
UNIDAD V. OXIDO REDUCCION.
POTENCIAL ESTANDAR Y COMBINACION DE PARES.
El agente reductor Zn, junto con su producto de oxidación Zn+2, constituyen lo que se denomina
un par Zn+2/Zn y se encuentra en el mismo compartimiento durante el funcionamiento de la celda.
De igual forma la otra media-celda contiene un par formado por el agente oxidante y su producto
de reducción (Cu+2, Cu).
Cada par tiene una capacidad intrínseca de aceptar electrones. A esta capacidad se le puede
asignar un valor numérico denominado potencial de reducción.
Si dos pares se combinan en una celda, el par con mayor potencial de reducción proporciona el
agente oxidante y acepta electrones en su electrodo. La fuerza determinante de la circulación de
la corriente, es la diferencia algebraica de los dos potenciales de reducción y es numéricamente
igual al voltaje de la celda galvánica, es decir, ∆E0 = E0catodo – E0anodo.
Un aspecto importante es que el voltaje de una celda galvánica depende tanto de las sustancias
químicas que intervienen en la reacción, como de sus concentraciones y también de la
temperatura.
UNIDAD V. OXIDO REDUCCION.
POTENCIAL ESTANDAR Y COMBINACION DE PARES.
Para facilitar la comparación de las diferentes celdas galvánicas, cada una debe ser
medida bajo cierto conjunto de condiciones normales de concentración y temperatura.
Las condiciones normales elegidas son: 1M de concentración para todos los materiales
solubles, 1 atm para todos los gases y para los sólidos su forma más estable a 25 grados
centígrados.
Al potencial medido bajo estas condiciones se le conoce como potencial estándar de la
celda, cuyo símbolo es E0. En la siguiente tabla se puede apreciar una lista de pares con
sus respectivos potenciales estándares.
Por ejemplo, un par con un potencial estándar de reducción grande y positivo, como el
(Au+/Au), es fuertemente oxidante.
UNIDAD V. OXIDO REDUCCION.
POTENCIAL ESTANDAR Y COMBINACION DE PARES.
UNIDAD V. OXIDO REDUCCION.
CALCULO DEL POTENCIAL DE UNA CELDA.
El potencial de una celda está dado por ∆E0. Por ejemplo, la tabla anterior muestra que el
potencial estándar de la celda Zn+2/Zn es -0,763 volts y la magnitud del potencial estándar
de la celda Cu+2/Cu es +0,337 volts. Estas dos reacciones se deben combinar de manera
que el zinc metálico aparezca al lado izquierdo y el cobre metálico al lado derecho. Por lo
tanto necesitamos invertir la dirección de la primera semirreacción, invirtiendo por
consiguiente el signo de su potencial estándar. Esto es:
(Zn+2/Zn es -0,763 volts E0 = -0,763 volts) x (-1) = Zn/Zn+2 es +0,763
Cu+2/Cu es +0,337 volts E0 = +0,337 volts
De manera que ∆E0 = +0, 337 volts –(-0,763 volts) = 1,1 volts.
El signo positivo de ∆E0 calculado significa que la dirección espontánea de la reacción es
de izquierda a derecha, tal como está descrita.
UNIDAD V. OXIDO REDUCCION.
CRITERIO DE ESPONTANEIDAD.
Veamos como se relaciona E0, con algunas cantidades termodinámicas, tales como ∆G0 y
K. En una celda electroquímica la energía química se transforma en energía eléctrica que,
en este caso, es el producto de la fuerza electromotriz de la celda por la carga eléctrica
total (en coulombios) que pasa a través de la celda:
Energía eléctrica = fem x carga total
Energía eléctrica = voltios x coulombios
Energía eléctrica = Joules.
Ahora la carga eléctrica total, está determinada por el número de moles de electrones (n),
que pasan a través del circuito:
Carga total = n.F
Donde F, la constante de Faraday, es la carga eléctrica contenida en 1 mol de electrones.
Experimentalmente se ha estimado que 1 Faraday es igual a 96.485,3 coulombios.
UNIDAD V. OXIDO REDUCCION.
CRITERIO DE ESPONTANEIDAD.
Dado que la Energía eléctrica de una celda se puede aprovechar para hacer trabajo, es
decir:
Energía eléctrica = Weléctrico
y dado que:
Wmax = -voltios x carga total
Wmax = -Weléctrico
Y como ya dijimos que:
Carga total = n.F
Wmax = -n.F .Ecelda
También se sabe que:
∆G = Wmax Entonces, ∆G = -n.F .Ecelda
UNIDAD V. OXIDO REDUCCION.
CRITERIO DE ESPONTANEIDAD.
Teniendo en cuenta que, ∆G = -n.F .Ecelda en condiciones estándar, ∆G0 = -n.F .E0celda.
Por otro lado también se sabe que ∆G0, puede representarse como sigue:
∆G0 = -R.T.Ln(K)
Entonces se puede decir:
-n.F .E0celda = -R.T.Ln(K)
Y
E0celda = R.T.Ln(K)/ n.F
Dando los valores de F = 96.500 coulombios, R = 8,314 J/K.mol, T = 298 K y expresando
todo en logaritmo base 10, la expresión anterior queda:
E0celda = (0,0592 V/n).logK
UNIDAD V. OXIDO REDUCCION.
CRITERIO DE ESPONTANEIDAD.
De manera que conociendo cualquiera de las tres cantidades, ∆G0, K o E0celda,
es posible calcular las otras dos cantidades. Además se puede predecir la
espontaneidad de una reacción. Veamos el siguiente cuadro:
∆G0
K
E0celda
Reacción en condiciones de
estado estándar
Negativo
>1
Positivo
Espontánea
Cero (0)
=1
Cero (0)
En equilibrio
Positivo
1<
Negativo
Espontánea en dirección
opuesta.