TEMA 1. Iteraciones. % Hemos aprendido que “para resolver una

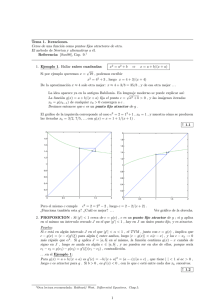
TEMA 1. Iteraciones.
% Hemos aprendido que “para resolver una ecuación en x, se despeja la x y se evalúa la
expresión que resulta”. El siguiente ejemplo nos hará revisar ese esquema.
Ejemplo 1. Comparar las siguientes ecuaciones, y hallar sus soluciones:
2x = 1 − x
2x = x2 − 1
,
, (x > 0),
2x = e−x
Con las dos primeras no hay problema:
√
x = 1/3 = 0.3333 ,
x = 1 + 2 = 2.4142 ,
pero en la tercera . . . ??
Aunque en ese caso no es posible despejar x , basta comparar las gráficas y = x , y = e−x /2 , para
ver que hay exactamente una solución x = α , que es el único punto fijo de g(x) = e−x /2 :
iterando g(x) = e!x / 2
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
!0.1
!0.2
!0.2
0
0.2
0.4
0.6
0.8
1
Las lineas de trazos muestran la siguiente operación:
partiendo de la abscisa x0 = 1/2 , ir a la nueva abscisa x1 = g(x0 ) .
Al continuar ese proceso: xk = g(xk−1 ) , vemos cómo las xk tienden al punto fijo.
(a la izquierda de la figura, limitada ahora a la zona de interés, vemos los valores que van saliendo)
x0 = 0.5
0.3033
0.3692
0.3456
0.3539
0.3510
0.3520
0.3516
0.3518
0.3517
0.3517
iterando g(x) = e!x / 2
0.38
0.36
0.34
0.32
0.3
0.3
0.32 0.34 0.36 0.38
0.4
0.42 0.44 0.46 0.48
0.5
√
√
% Esto nunca llega a ser exacto, pero 2 = 1.41 . . . tampoco! De x = 2 sabemos que cumple
x2 = 2 exactamente, pero de nuestro α también: 2α = e−α , exactamente.
Reflexionar sobre la palabra “resolver”: para ciertos usos, queremos un desarrollo decimal,
con cierto margen de error; para otros, la ecuación misma es lo que vale.
Generalicemos: ¿funcionará este método para resolver x = ce−x para todo c > 0 ?
Pues NO: si tomamos c = 3 , vemos que el punto fijo está cerca de x0 = 1 , pero al tomar sus
imágenes iteradas xk = g(xk−1 ) , lo que vemos es que en lugar de acercarse al punto fijo α , . . .
1
!x
iterando g(x) = 3 e
3.5
3
2.5
. . . se alejan hacia un ciclo
con a < α < b .
!
2
b = g(a)
,
a = g(b)
1.5
1
0.5
0
!0.5
!0.5
0
0.5
1
1.5
2
2.5
3
3.5
¿Qué hace diferentes a esos dos casos?
PROPOSICION. Sea α = g(α) , un punto fijo para la función derivable g .
• Si en algún entorno J = [α − h, α + h] se tiene |g " (x)| < 1 , entonces las iteradas xk = g(xk−1 ) de
cualquier x0 ∈ J tienden a α ; decimos entonces que el punto fijo α es un atractor.
• Si por el contrario |g " (x)| > 1 en J , entonces las iteradas se alejan de α , al menos mientras
permanezcan en J .
Prueba: Mientras sea xk ∈ J , el TVM ⇒ |xk+1 − α| = |g(xk ) − g(α)| < |xk − α| en el
primer caso, lo contrario en el otro. Esto prueba, por inducción sobre k , la 2a. afirmación;
para la 1a. falta probar que ∃r < 1 tal que |xk+1 − α| < r|xk − α| .
Pero basta tomar |g " (α)| < r0 < 1 para tener algún δ > 0 tal que
|x − α| < δ
x∈J
⇒
⇒
|g(x) − α| < r0 |x − α| , y de ahı́, usando |g " | < 1 , deducir1 que
|g(x) − α| < r|x − α| , para algún r < 1 (que depende de r0 , δ, h) .
g(x) = 3 e!x ; en rojo: pendiente > 1
Por ejemplo, g(x) = ce−x cumple
g " (x) = −g(x) ,
3
2.5
luego su punto fijo α cumple
la hipótesis si y sólo si es α < 1 ,
es decir si c < e = 2.7183 :
2
1.5
1
0.5
0
EJEMPLO PARA TRABAJAR
HASTA LA CLASE SIGUIENTE
E 1.1
!0.5
0
0.5
1
1.5
2
2.5
√
Vamos a hallar aproximaciones cada vez mejores de la raı́z cuadrada α = m
siguiente: al tomar una aproximación inicial a y escribir m = a2 + b , vemos que
α2 = a2 + b
3
3.5
del modo
(α + a)(α − a) = b
⇒
de donde es inmediato deducir que α es punto fijo de
g(x) = a + b/(x + a)
.
Hacerlo, y probar que |g " (α)| < 1 , usando que α, a > 0 .
√ √ √
En cada uno de los casos α = 2, 3, 5 , tomar como a el entero más cercano, y luego
• dibujar aproximadamente la función g(x) a iterar, y usando la calculadora,
√
• hallar iteradas xk = g(xk−1 ) de x0 = a , hasta que 4 dı́gitos más coincidan con los de m.
[•∗ ] Si g tiene punto fijo α , probar que la condición |g " (α)| < 1 implica, sin más hipótesis sobre g , la
existencia de un J = [α − h, α + h] en el que las iteradas de cada punto tienden a α.
Pero esa condición no es necesaria para un atractor: estudiar el caso g(x) = e1−x , y comprobar2 que el
punto fijo x = 1 , en el que g " = −1 , es atractor, aunque lentı́iiisimo.
1 Basta
un dibujo para convencerse.
pero se puede también probar que es ası́ usando el desarrollo de Taylor de g ◦ g en x = 1.
2 Experimentalmente,
2
• Para el problema encontrado al iterar g(x) = 3e−x , hay un remedio sencillı́simo: iterar en su lugar
h = g −1 , porque α también es fijo para h , y h" (α) = 1/g " (α) .
El problema es lo lento que va:
iteradas de h(x) = log(3/x)
1.1
1.05
1
0
5
10
15
20
25
30
35
40
45
50
diferencias: | xk ! xk!1 |
0.1
0.05
0
0
5
10
15
20
25
30
35
40
45
50
El por qué nos lo da la prueba de la PROPOSICION: el error xk − α se multiplica cada vez por
un factor h" (ξ) ≈ h" (α) , y en este caso es
g " (α) = −g(α) = −1.0499 , luego |h" (α)| = 0.9525 , y log10 |h" (α)| ≈ −1/47 ,
por eso hacen falta ≈ 50 iteradas de h para ganar un dı́gito de precisión !!
Moraleja: la derivada de la función que iteramos deberı́a ser “pequeña” en el atractor α .
• Por otra parte, el signo de h" (α) = −0.95 es el que hace “girar” a las iteraciones de h(x). Al estar
α entre cada iterada y su imagen, tenemos cada vez una cota del error |xk − α|.
√
Comparar con la “escalera” (ver figura siguiente, a la izquierda) del caso 3 en el ejercicio E1.1 ,
donde se tiene g " (α) > 0 .
Lo bueno es que hay muchos posibles iteradores que fijen la solución de una ecuación dada:
Ejemplo 2. Los ceros de la función F (x) = x2 − a son puntos fijos de cada una de estas funciones:
g1 (x) = a/x , g2 (x) = (x + a/x)/2
√
√
La primera no sirve como iterador, porque g1" ( a) = −1 ; pero la segunda . . . g2" ( a) = 0 .
2.1
de g y de g2 desde x0 = 2
Iteradas de g(x) =Iteradas
2 ! 1/(x+2)
0
g1(x) = 3/x , g2(x) = (x+3/x) / 2
10
3
2.05
2.8
!2
distancia de x al atractor
2
1.95
2.6
2.4
!4
10
2.2
k
1.9
10
1.85
1.8
1.75
2
1.8
!6
10
1.6
1.4
!8
10
1.7
1.2
1.65
1.6
1.6
1
!10
1.7
1.8
10
0
1.9
2 2
4
3
2.16
8
1
1.5
2
g1(x) = 3/x , g2(x) = (x+3/x)/2
Iteradas de g y de g2
0
10
distancia de xk al atractor, con x0 = 2
3
Vemos en el logplot de la derecha cómo en el caso de
2.5
g(x) = 2 − 1/(x + 2)
√
el error residual xk − α , con α = 3 , se multiplica
cada vez aproximadamente por la misma constante:
2
g " (α) = 1/13.9 .
Por eso sus log10 son aproximadamente función lineal de k ,
y se ven alineados (convergencia lineal al atractor).
1.5
!2
10
!4
10
!6
10
!8
10
1
Como vemos también allı́ (las estrellas verdes),
1
1.5
2
los errores de la g2 (x) = (x + 3/x)/2
disminuyen mucho más rápido, porque
! "
g "" (α)
g2 (α) = 0 √
⇒ g2 (x) = α + 2
(x − α)2 + . . .
g2 (α) = α = 3
2
!10
10
0
2
4
6
8
k
⇒
1
xk+1 − α ≈ √ (xk − α)2
2 3
¿Cómo conseguir iteradores ası́ de buenos? La idea general es:
Si F (α) = 0 , cada g(x) = x − k(x)F (x) fija α , y α es atractor si |1 − k(α)F " (α)| < 1 .
Lo ideal es g " (α) = 0 , como se consigue con el
método de Newton: g(x) = x − F (x)/F " (x)
g(x) = la abscisa donde corta al eje x la recta tangente en (x, F (x)) a la gráfica de F .
Ejemplos 
de Newton3 :
 (x + a/x)/2
g(x) = (1 + log c − log x)/(1 + 1/x)

x(2 − ax)
10
2

 x2 − a (ver gráfico de la izquierda)
si F (x) = x + log(x/c) (equivale al Ejemplo 1)

a − 1/x
g(x) = (x+3/x)/2
1.5
1
0.5
5
0
!0.5
!1
0
!1.5
!2
F(x) = x2!3
!2.5
!3
0
0.5
1
1.5
2
!5
!8
!6
!4
!2
0
2
4
6
8
• En los ejemplos anteriores es muy fácil tomar x0 en la cuenca del atractor buscado, pero no siempre
la situación es tan limpia: observar por ejemplo F (x) = sen(x) − cx (gráfico de la derecha).
Puede verse cuál es (para las iteraciones Newton) la cuenca inmediata del punto α > 0 en el que
F se anula; si escogemos x0 ligeramente fuera de ella, podemos terminar en cualquier parte . . .
Por eso hay que tener bien localizado el cero buscado de F (x) , y disponer de métodos de arranque
más seguros hasta llegar cerca de él, como por ejemplo
Bisección: Dados dos puntos a, b entre los cuales la función (continua) F cambia de signo, reemplazar uno de ellos con el punto medio (a + b)/2 , de modo que F siga cambiando de signo.
• ¿Cuánto podemos acercarnos al punto buscado? Lo que permita la precisión de la calculadora que
usemos: cuando F (x)/F " (x) llegue a ser demasiado pequeño en comparación con x , la calculadora
dirá que x − F (x)/F " (x) = x , y habremos llegado en la práctica 4 al punto fijo de g .
3 El
último es el algoritmo “multiplicar para dividir”, que aproxima 1/a sin hacer divisiones.
sobre eso en los próximos dı́as.
4 Más
4
E 1.2
Considerar la función
EJEMPLO PARA TRABAJAR
HASTA LA CLASE SIGUIENTE
F (x) = sen(x) − cx + d ,
donde c, d ∈ (0, 1) son constantes dadas (por ejemplo, producidas al azar por la tecla RAN# de
alguna calculadora). El objetivo es hallar el menor α > 0 en el que F (α) = 0 .
Probar que hay al menos un tal α > 0 , y luego escribir seudocódigo (es decir, un plan
traducible inmediatamente en código), que incluya las siguientes etapas:
• Localización: usando bisección, llegar a un x0 que pueda estar en la cuenca de α .
• Aproximación: usando Newton, acercarse a α hasta la precisión deseada. Hará falta algún
criterio de parada, y recordar que la precisión está limitada por la calculadora que usemos.
• Recuperación: qué hacer si las iteradas xk escapan de la zona prevista.
[•∗ ] Usando el desarrollo de Taylor de g , hemos visto qué relación hay entre los sucesivos xk − α cuando
iteramos una g que cumple g " (α) = 0 '= g "" (α) .
Probar ahora que el iterador g(x) = x − F (x)/F " (x) cumple esas condiciones si, en el punto que tratamos
de aproximar, la función F (x) tiene derivada F " (α) '= 0 = F (α) .
Usar el desarrollo de Taylor de F para estudiar qué ocurre si F " (α) = 0 .
Tema 1: BIBLIOGRAFIA Y COMENTARIOS.
Terminaremos de ver este Tema en el Laboratorio, mientras tratamos de convertir en código
las ideas vistas en clase (como se apunta en el ejercicio E 1.2), y de experimentar con ellas.
Las ideas esenciales están contenidas en el Capı́tulo 9 de nuestro texto principal
Sanz-Serna: Diez Lecciones de Cálculo Numérico
que tiene, entre otras muchas, la rara virtud de ser breve5 .
Vamos a ver en el Laboratorio alguna variante más de esas ideas.
Quizá procede este comentario:
La escritura, como medio de transmisión del saber, parece llevar unida la tendencia a multiplicar las páginas, los nombres, las maneras diversas de exponer una misma idea. Quien mire
las que dedican muchos libros de Cálculo Numérico al tema que nos ocupa, puede sacar a
veces la impresión de que hay docenas de “métodos posibles”. Y parece que esa tendencia se
contagia fácilmente al buen estudiante, que puede llegar a medir el éxito de su esfuerzo por
la cantidad de nombrecillos a los que ha conseguido asociar alguna idea.
Y sin embargo, la Historia del pensamiento es una batalla continua por reducir la complejidad
con que nos llegan los datos, los problemas, las propuestas de solución de los mismos. Podemos decir en alabanza de la Fı́sica que allı́ la búsqueda de “teorı́as unificadas” ha convertido
en un lugar común esta verdad general de las Ciencias: que el objetivo es llegar a ver como
ramas de un mismo árbol el mayor número posible de ideas a primera vista diversas.
Por ejemplo, en este Tema 1 las ideas diferentes son como mucho dos, las mismas que debe
aplicar cualquier predador: cómo acorralar a la presa, cómo saltar sobre ella . . .
5Y
como consecuencia –aunque menos importante– la de ser barato...
5