Ejemplos: Realización de Diagramas de Bode
Anuncio
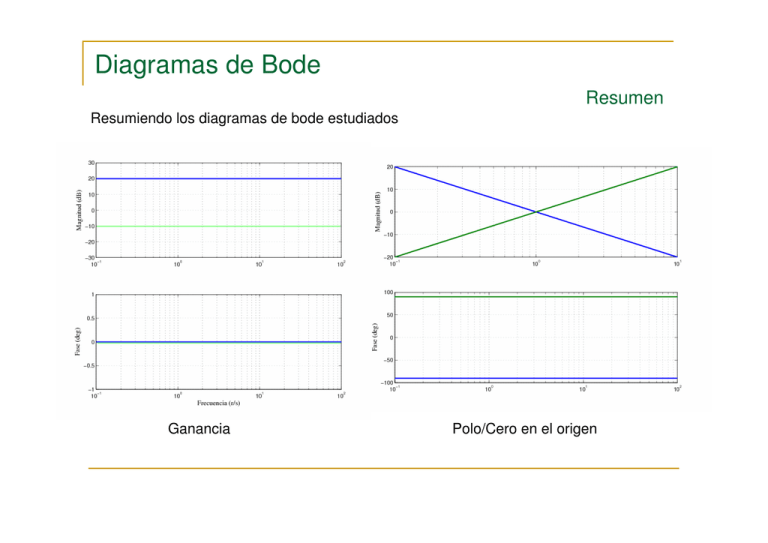
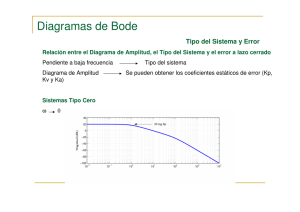
Diagramas de Bode Resumen Resumiendo los diagramas de bode estudiados Ganancia Polo/Cero en el origen Diagramas de Bode Resumen Polo en el eje real Cero en el eje real Diagramas de Bode Resumen Polos/Ceros conjugados Diagramas de Bode Ejemplos: Realización de Diagramas de Bode Separando cada uno de los factores y determinando su contribución según la frecuencia se tiene la siguiente lista. Baja Frecuencia Ganancia K = 10 (20log10=20 dB) Magnitud Alta Frecuencia Magnitud Polo en el eje real (ω1 = 1) Magnitud; Fase Cero en el eje real (ω2 = 10) Magnitud; Fase Polo en el eje real (ω3 = 100) Magnitud; Fase A partir de allí se construye el diagrama partiendo a baja frecuencia y añadiendo factor por factor a medida que van apareciendo sus contribuciones. Diagramas de Bode Ejemplos: Realización de Diagramas de Bode Diagramas de Bode Ejemplos: Realización de Diagramas de Bode Separando cada uno de los factores y determinando su contribución según la frecuencia se tiene la siguiente lista. Baja Frecuencia Ganancia K = 40 (20log40=32 dB) Magnitud Magnitud; Fase Alta Frecuencia Magnitud Polo en el origen Magnitud; Fase Polo en el eje real (ω1 = 1) Magnitud; Fase Cero doble eje real (ω2 = 10) Magnitud; Fase Polo en el eje real (ω3 = 100) Magnitud; Fase A partir de allí se construye el diagrama partiendo a baja frecuencia y añadiendo factor por factor a medida que van apareciendo sus contribuciones. Diagramas de Bode Ejemplos: Realización de Diagramas de Bode Diagramas de Bode Ejemplos: Realización de Diagramas de Bode Diagramas de Bode Identificación Frecuencial Al igual que la Identificación Temporal, la Identificación Frecuencial permite obtener la aproximación de la función de transferencia de un proceso a partir del conocimiento de su respuesta. En este caso la identificación se basará en el conocimiento de la respuesta frecuencial representada a través de un diagrama de bode. PROCEDIMIENTO Análisis a baja y alta frecuencia Diagrama de Bode Asintótico Aproximación de la Función de Transferencia Diagramas de Bode Identificación Frecuencial. Ejemplos ANÁLISIS Baja Frecuencia Magnitud Fase sin pendiente (20 dB) 0 (grados) Conclusión Tipo Cero y 20log (K) = 20 db Alta Frecuencia Magnitud Fase pendiente (-40 dB) -180 (grados) Conclusión (n-m) = 2 Dos polos más que ceros Forma de las curvas Tanto la magnitud como la fase son siempre decrecientes solamente hay polos Forma aproximada de G(s) Diagramas de Bode Identificación Frecuencial. Ejemplos Diagramas de Bode Identificación Frecuencial. Ejemplos ANÁLISIS Baja Frecuencia Pendiente Fase (-20 dB/dc) -90 (grados) Conclusión Tipo I y 20log (K) = - 4 db K = 0,63 Alta Frecuencia Magnitud Fase pendiente (-60 dB) -270 (grados) Conclusión (n-m) = 3 Tres polos más que ceros Forma de las curvas La fase aumenta ligeramente a baja frecuencia y m tiende a cero un cero. Debe haber otro polo para que sumado al del origen y a los conjugados sean 4. Forma aproximada de G(s) Diagramas de Bode Identificación Frecuencial. Ejemplos