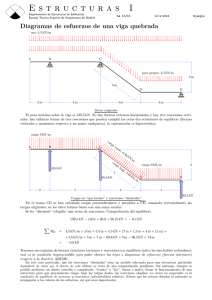
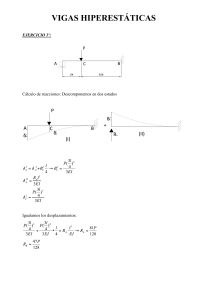
La viga continua de la figura tiene cada tramo de sección constante
Anuncio
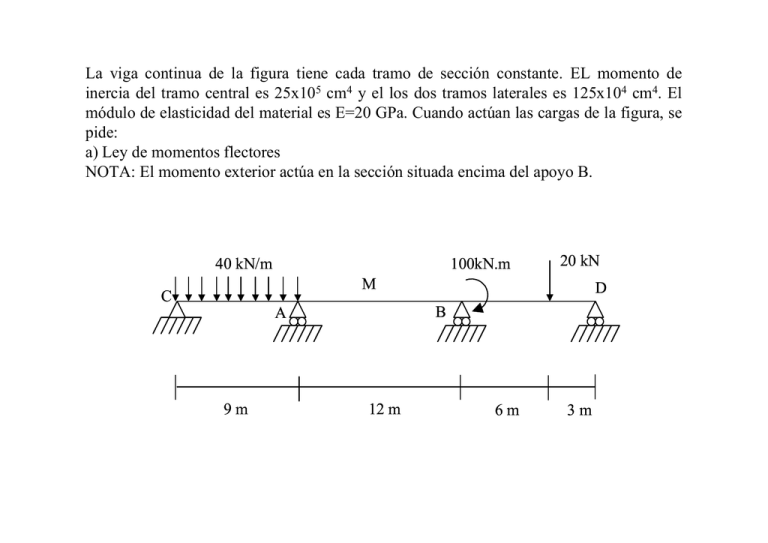
La viga continua de la figura tiene cada tramo de sección constante. EL momento de inercia del tramo central es 25x105 cm4 y el los dos tramos laterales es 125x104 cm4. El módulo de elasticidad del material es E=20 GPa. Cuando actúan las cargas de la figura, se pide: a) Ley de momentos flectores NOTA: El momento exterior actúa en la sección situada encima del apoyo B. 40 kN/m 100kN.m 20 kN M C B A 9m D 12 m 6m 3m M1 C q A1 M1 M2 M1 P B2 B1 A2 M3 D G IAB=2IAC=2IBD Si aislamos la rebanada B, y para que se satisfaga el equilibrio de la misma, los momentos deben cumplir: M2 M M3 M2+M3=100 Ec.(1) Apoyo A: M1 9 M 12 M 12 40 ⋅ 9 3 − = 1 + 2 24 EI AC 3 EI AC 3 EI AB 6 EI AB Apoyo B: M 3 9 20 ⋅ 6 ⋅ 3 ⋅ (9 + 3) M 1 ⋅ 12 M 2 12 − − =− − 6 EI AB 3EI AB 3EI BD 6 ⋅ 9 EI AD 5 ⋅ M 1 + M 2 = 1215 Ec .( 2) M 1 + 2 M 2 = 3 ⋅ M 3 + 80 M1=237,3 kN.m M2=28,5 kN.m Ec .(3) M3=71,5 kN.m Ley de momentos flectores (momento flector positivo aquel que produce compresión en la fibra superior y tracción en la inferior): Tramo CA: La reacción en C es igual a 180-237,3/9=153,6 kN y va dirigida hacia arriba. Tomando como x la distancia al extremo C de una sección genérica de este tramo, se tiene: x2 M ( x ) = 153,6 ⋅ x − 40 ⋅ 2 que se anula para x=7,68 m y presenta un máximo en el punto x=3,84 m de valor 294,9 kN.m. Tramo AB: Al no existir cargas aplicadas directamente (solo actúan los momentos en las secciones extremas), la ley de momentos flectores será lineal, con valores extremos de -237,3 kN.m, a la izquierda, y -28,5 kN.m a la derecha. Tramo BD: Tomando como origen de abcisas el extremo B, y teniendo en cuenta que la reacción en B2 es 1,27 kN, se tiene: 0 ≤ x ≤ 6 M ( x ) = 71,5 − 1,27 ⋅ x 6 ≤ x ≤ 9 M ( x ) = 71,5 − 1,27 ⋅ x − 20 ⋅ ( x − 6 ) 237,3 kN.m 7,68 m 3,84 m C 28,5 kN.m D A B 71,5 kN.m 294,9 kN.m 63,9 kN.m