+(2
Anuncio
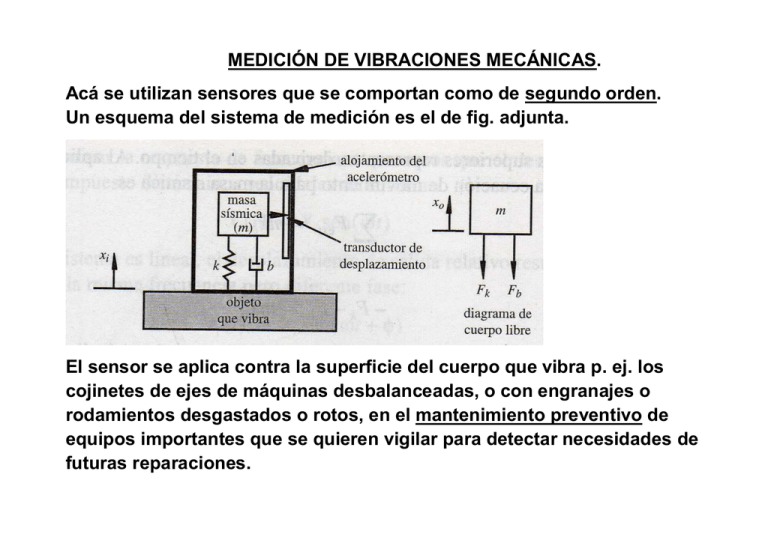
MEDICIÓN DE VIBRACIONES MECÁNICAS. Acá se utilizan sensores que se comportan como de segundo orden. Un esquema del sistema de medición es el de fig. adjunta. El sensor se aplica contra la superficie del cuerpo que vibra p. ej. los cojinetes de ejes de máquinas desbalanceadas, o con engranajes o rodamientos desgastados o rotos, en el mantenimiento preventivo de equipos importantes que se quieren vigilar para detectar necesidades de futuras reparaciones. El sensor consiste en una caja o alojamiento dentro del cual hay una masa llamada “masa sísmica” que sólo se puede mover en una dirección preestablecida, determinada por unas guías no mostradas en el esquema. Esa dirección constituye el eje del sensor y es la dirección según la cual se medirá la vibración; en la fig. ésta es: xi. La masa está sujeta a la caja mediante un elemento elástico (ménsula) que por no ser perfectamente elástico debe representarse por un resorte ideal (sin pérdida de energía) y un amortiguador (el que produce las pérdidas de energía). Cuando el alojamiento se sujeta a la superficie de una máquina que vibra, esto hará que la masa sísmica vibre también. Mediante un transductor de desplazamiento se conoce (se mide) el desplazamiento relativo de la masa respecto del alojamiento, que llamaremos: xr. Entonces: xi es la señal de entrada, vibración o desplazamiento que se quiere medir xr es la señal de salida o respuesta del sensor. El desplazamiento total o absoluto de la masa x0 es: x0 = xi + xr (1) Para plantear la ec. diferencial del movimiento de la masa sísmica “m” se hace el diagrama de cuerpo libre de la masa y se aplica la 2º ley de Newton, recordando que ésta es: ∑ Fuerzas = masa x aceleración (absoluta) Las fuerzas que actúan sobre la masa son las debidas al elemento elástico o sea resorte y amortiguador: a) Fuerza debida al resorte: Fk = - k . xr k : constante del resorte, Fk es una fuerza proporcional al desplazamiento (relativo) de la masa y de signo contrario ( se opone al desplazamiento). b) Fuerza debida al amortiguador: Fb = - b . d xr /dt b: constante de amortiguación, Fb es una fuerza proporcional a la velocidad (relativa) de la masa y de signo contrario La aceleración absoluta resulta de derivar dos veces el desplazamiento respecto al tiempo ( la ec. 1) : d2x0 /dt2 = d2 xi /dt2 + d2xr /dt2 (2) Entonces aplicando la 2º ley de Newton queda: m d2xr /dt2 + b . d xr /dt + k . xr = - m d2 xi /dt2 (3) Dividiemos todo por K : m/k . d2xr /dt2 + b/k . d xr /dt + xr = - m/k. d2 xi /dt2 (4) La forma tipo es : (1/n2) d2y/dt2 +(2n) dy/dt + y = Kx (5) K: sensibilidad estática , x: entrada Entonces en nuestro caso resulta: n= (k/m) ½ b/2.(km)1/2 (6) Notar que n y son valores establecidos en el diseño del instrumento, o sea los fabricantes pueden darles lo valores que sean mejores. Como las vibraciones son periódicas, podemos asumir que están constituidas por sumas de términos sinusoidales o armónicos de distintas frecuencias (desarrollo de Fourier) o sea que sin pérdida de generalidad puedo poner: xI = Xi sen t , (7) en que Xi es la amplitud o valor máximo del desplazamiento por vibración que se quiere medir y la frecuencia de la vibración. Cada tipo de defecto mecánico genera vibraciones de determinadas frecuencias, por ejemplo el desbalanceo produce una vibración cuya frecuencia es la velocidad de giro en rad/ segundo. Entonces: dxi /dt = Xi cos t , d2 xi /dt2 = - Xi sent Y resulta: Kx = - m/k (- Xi sent) = (mkXi sent (8) O también: Kx = (n)2 Xi sent Reemplazando en la ec. (5) (1/n2) d2y/dt2 +(2n) dy/dt + y = (n)2 Xi sent Ahora podemos aplicar lo que vimos sobre respuesta de un sensor de segundo orden a una entrada sinusoidal, tipo: A sen t ENTRADA: A sen t SALIDA: y(t) dada por la expresión: (9) Con dada por la expresión: (10) En nuestra aplicación la “entrada” o sea el: “ k A sen t ” es el término que aparece del otro lado del igual, ahora: “ k A sen t ” = (n)2 Xi sent Nos interesa es ver como es la relación Xr / Xi entre amplitud medida Xr y amplitud a medir Xi : (11) La gráfica que sigue es la respuesta en amplitud de vibración: Xr / Xi en función de : n . Lo ideal es que Xr / Xi = 1 para que Xr = Xi o sea cero error dinámico para toda En la fórmula anterior y del gráfico resulta que si n es muy grande (tiende a infinito) el cociente tiende a la unidad. Entonces y para poder llegar a medir con grandes conviene que el sensor se construya con n lo menor posible, y con = 0.707 Lo que estudiamos hasta ahora fue la medida de la amplitud o intensidad de la vibración, cosa que interesa no solo en máquinas también, también en el estudio de sismos, actividad de volcanes etc. ACELERÓMETROS Otra magnitud que interesa mucho es la medida de aceleraciones. El análisis de los acelerómetros es muy similar a lo anterior. De la expresión: d2 xi /dt2 = - Xi sent se deduce que la amplitud de aceleración de la entrada es : Xi Si reordenamos la ec (11) resulta: De modo que la amplitud de la aceleración de entrada se puede expresar como La respuesta de amplitud de aceleración es como se ve en la fig. siguiente. Si se diseña el acelerómetro de modo que Ha() valga casi 1, sobre un gran rango de frecuencias, entonces: Xi . 2 = ( n2) Xr O sea la amplitud de la aceleración de entrada ( a medir) estará dada por la amplitud del desplazamiento relativo Xr multiplicado por la constante del instrumento: n2 El rango de frecuencias que mide el sensor es máximo si se elige el n tan grande como sea constructivamente posible y el = 0.707.