ESTRUCTURAS DE EMPAQUETAMIENTO COMPACTO
Anuncio
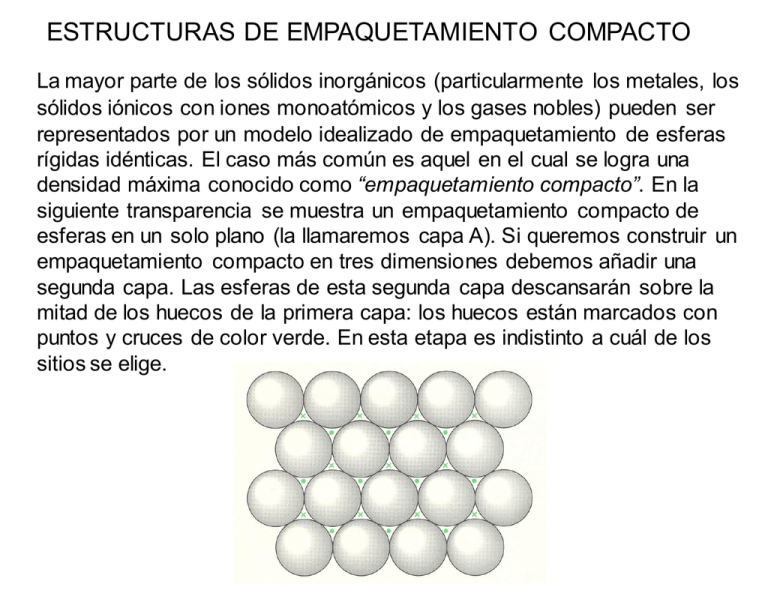
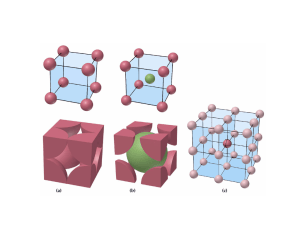
ESTRUCTURAS DE EMPAQUETAMIENTO COMPACTO La mayor parte de los sólidos inorgánicos (particularmente los metales, los sólidos iónicos con iones monoatómicos y los gases nobles) pueden ser representados por un modelo idealizado de empaquetamiento de esferas rígidas idénticas. El caso más común es aquel en el cual se logra una densidad máxima conocido como “empaquetamiento compacto”. En la siguiente transparencia se muestra un empaquetamiento compacto de esferas en un solo plano (la llamaremos capa A). Si queremos construir un empaquetamiento compacto en tres dimensiones debemos añadir una segunda capa. Las esferas de esta segunda capa descansarán sobre la mitad de los huecos de la primera capa: los huecos están marcados con puntos y cruces de color verde. En esta etapa es indistinto a cuál de los sitios se elige. En la siguiente diapositiva se ha colocado una segunda capa de esferas de color verde (capa B) sobre los huecos marcados con una cruz (sería equivalente en este momento si se lo hiciera sobre los marcados con un punto). Si quisiéramos añadir una tercer capa, habría dos posiciones posibles: (i) podría ir directamente sobre las posiciones de la capa A y si repitiéramos secuencialmente este apilamiento tendríamos un empaquetamiento ABABAB que se conoce como “empaquetamiento hexagonal compacto” (ehc, o hcp del inglés “hexagonal close packing”). (ii) La otra posibilidad sería que la tercer capa vaya sobre los sitios marcados con puntos. Esta tercer capa que llamaremos C, no está directamente sobre ninguna de las dos anteriores. Si esta secuencia de apilamiento se repitiera, tendríamos un empaquetamiento de tipo ABCABC… que se conoce como “empaquetamiento cúbico compacto” (ecc o ccp del inglés “cubic close packing”). Los nombres hexagonal y cúbico que reciben estas estructuras se derivan de la simetría resultante. Esta simetría puede apreciarse en la transparencia siguiente. En la b se puede ver el empaquetamiento ABAB… que da lugar a la simetría hexagonal (ech) mientras que en la c se observa el empaquetemiento ABCABC…. que da lugar a la simetría cúbica (ecc). Empaquetamiento Compacto de esferas Apilamiento de capas ABAB Estructura hexagonal Apilamiento de capas ABC Celda unidad cúbica EMPAQUETAMIENTO HEXAGONAL COMPACTO Capa a Capa b Vista de arriba Capa a Número de coordinación = 12 Eficacia = 74 % EMPAQUETAMIENTO CÚBICO COMPACTO Capa a Capa c Capa b Vista de arriba Capa a Número de coordinación = 12 Eficacia = 74 % Cúbico simple Cúbico centrado en el cuerpo Empaquetamiento cúbico compacto (Cúbico centrado en las caras) Empaquetamiento hexagonal compacto Celda unidad Cúbico Simple Red Ejemplo Polonio metálico Cúbico simple Cúbico Centrado en el cuerpo Uranio metálico Cúbico centrado en el cuerpo Cúbico centrado en las caras Oro metálico Cúbico centrado en las caras TIPOS DE CELDAS CÚBICAS Cúbica simple Cúbica centrada en el cuerpo Cúbica centrada en las caras SpherePacking.cdf CubicClosePackingCube.cdf CELDA CÚBICA SIMPLE CELDA CÚBICA SIMPLE Arista (a) = 2 x radio (r) a r Número de coordinación = 6 Átomos por celda = 8 x 1/8 = 1 Vocupado /Vcelda = (4/3 π r3)/a3 = π/6 = 0,52 Eficacia del empaquetamiento = 52 % CELDA CÚBICA CENTRADA EN LAS CARAS CELDA CÚBICA CENTRADA EN LAS CARAS Número de coordinación = 12 Átomos por celda = (8 x 1/8) + (6 x ½) = 4 4r a (4.r)2 = a2 + a2 Vocupado /Vcelda = 4.(4/3 π r3)/a3 = 0,74 Eficacia del empaquetamiento = 74 % CELDA CÚBICA CENTRADA EN EL CUERPO Capa a Capa b Capa a CELDA CÚBICA CENTRADA EN EL CUERPO Número de coordinación = 8 Átomos por celda = (8 x 1/8) + 1 = 2 b2 = a2 + a2 c b a c2 = a2 + b2 = 3.a2 c = 4.r = (3.a2)1/2 Vocupado /Vcelda = 2.(4/3 π r3)/a3 = 0,68 Eficacia del empaquetamiento = 68 % Estas estructuras de empaquetamiento compacto de esferas rígidas idénticas es adoptada por la mayoría de los sólidos monoatómicos, esto es los metales y los gases nobles. Sin embargo, en el caso de compuestos binarios del tipo AB, AB2, A2B donde A y B tienen tamaños distintos, es necesario describir lo que se llama formación de “sitios intersticiales”. En las trasparencias siguientes se describe la formación de “sitios intersticiales” octaédricos y tetraédricos en las redes de empaquetamiento compacto. En la mayor parte de los compuestos binarios iónicos en los cuales hay un ión grande (generalmente anión) y un ión pequeño (generalmente catión) de un tamaño adecuado como para ingresar en alguno de estos sitios intersticiales, ésta es la descripción adecuada de sus estructuras Cúbico centrado en las caras Huecos Octaédricos (Oh) y Tetraédricos (Td) Se puede deducir cuál debe ser la relación de radios r1/r2 para que un ión entre perfectamente en un sitio intersticial octaédrico. En la transparencia se muestra la geometría de un sitio octaédrico. En ella se puede ver que se cumple: 2(r1 + r2)2 = (2r2)2 ; de donde se deduce: r1 + r2 = 2 r2; y de aquí: r1/r2 = 0,414 Esta relación deducida para otros tipos de sitios se muestra en la transparencia siguiente. Relación límite de radios Celda unidad Lado =a Celda unidad 1/8 Celda unidad diagonal de la cara = a√2 diagonal del cubo = a√3 De esta manera, dependiendo de la estequiometría del compuesto binario y de la relación entre los radios del catión y el anión, éstos pueden adoptar distintas estructuras, las cuales se resumen en la siguiente tabla.