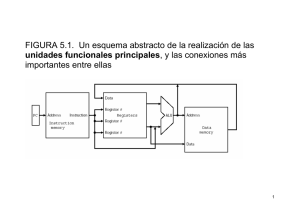
ALU

ELO311
Estructuras de Computadores Digitales
Unidad Aritmética
Tomás Arredondo Vidal
Este material está basado en:
material de apoyo del texto de David Patterson, John Hennessy,
"Computer Organization & Design", (segunda y tercera edición),
Morgan Kaufmann, CA. 2005
material del curso anterior ELO311 del Prof. Leopoldo Silva
www.wikipedia.org
Sumador sin Signo
Dos números sin signo, con ancho tres.
Con A0 y B0 los bits menos significativos.
Carry-in, que es una entrada del sumador, igual a
cero.
A2 A1 A0
+ B2 B1 B0
Co S2 S1 S0
Sumador sin Signo
Se realizan las sumas binarias, para cada par de
valores posibles para las entradas.
Se forma una tabla, en la que se han indicado los
valores de los operandos de entrada en decimal y
binario.
Se produce un resultado incorrecto cuando los bits
disponibles para el resultado no pueden acomodarlo
(overflow).
Sumador sin Signo
Ejemplo:
Operandos de largo tres A2A1A0 y B2B1B0
Resultado: CoS2S1S0
La señal Carry-out, que es una salida del sumador nos
permite detectar un resultado incorrecto (overflow)
para la suma de enteros sin signo.
Sumas y Restas con Signo
Se forma una tabla, en la que se han indicado los
valores de los operandos de entrada en decimal y
binario.
Dos números con signo, en complemento a dos
Con operandos de largo 3, no pueden representarse
los menores que -4 y los mayores que +3.
Se produce un resultado incorrecto cuando el signo de
ambos operandos es diferente del signo del resultado
(overflow).
El Carry-out, no determina esta condición, ya que
existen resultados correctos que tienen Carry-out igual
a uno.
Sumas y Restas con Signo (cont)
Ejemplo:
Operandos de largo tres A2A1A0 y B2B1B0
Resultado: CoS2S1S0
Overflow: Resultados con signo distinto de ambos operandos
Overflow: Resultados con signo distinto de ambos operandos
Sumas y Restas con Signo (cont)
La ecuación lógica para el overflow, puede obtenerse
en la última etapa del sumador con los bits de signo
de los operandos (A2, B2) y el bit de signo del
resultado (S2).
ov = overflow = A2 B2 S2' + A2' B2' S2
Para un sumador de 32 bits:
ov = overflow = A31 B31 S31' + A31' B31' S31
Comparaciones
Se forma una tabla para comparar dos números con
signo, para hacerlo se efectuará la resta entre ellos.
La condición se denomina LT (less than).
Se ingresan al sumador un número (A), y el
complemento uno del otro (~B).
Se fija Carryin en uno para que la situación A = B
entregue un resultado deseado (e.g. 1000).
Comparaciones (cont)
Ejemplo:
Operandos de largo tres A2A1A0 y B2B1B0
Resultado: CoS2S1S0
La zona A < B, se encuentra sobre la diagonal principal de la
matriz.
La condición A = B, es la diagonal principal, en la cual todos
los bits del resultado son ceros, y uno la reserva de salida.
-4
-3
-2
-1
0
1
2
3
Zona de
Overflow
Zona de
Overflow
Comparaciones (cont)
Existen dos zonas triangulares en las que se produce
overflow.
Una en que los signos de las entradas al sumador (no los
operandos) son ambos negativos, y el resultado es positivo.
La otra zona triangular caracteriza operandos de entrada al
sumador positivos y signo del resultado es negativo.
A es menor que B, si el signo del resultado es menos
y no hay overflow o si el signo del resultado es positivo
y se produce overflow.
Entonces la ecuación lógica puede escribirse:
LT = (A < B) = S2 ov' + S2' ov
Comparaciones de Números sin Signo
Condición less than unsigned (LTU).
Entonces la ecuación lógica para la condición LTU es:
LTU = ~Cout
Generación de Condiciones
Para un sumador de 32 bits, se puede construir la
siguiente tabla de verdad para las condiciones, en
función de las entradas A31, B31 y el Carry-in a esa
etapa, C31.
A31
B31
C31
Co
S31
Ov
LT
0
0
0
0
0
0
0
0
0
1
0
1
1
0
0
1
0
0
1
0
1
0
1
1
1
0
0
0
1
0
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
1
1
1
1
0
1
Unidad Aritmética
Las condiciones pueden escribirse en función de las entradas
a la última etapa del sumador:
ov = ( C31 ⊕ Co ) = C31Co' + C31'Co = (C31 diferente de Co)
LT = (A < B ) = ( S31 ⊕ ov ) = A31C31' + B31C31' + A31B31
Zero = ( A == B) = (S2 + S1 + S0)'
GE = ( A >= B) = ( A < B )' = (LT)' = greater or equal
NZ = ( A != B) = Zero' = (S31+ ...+ S2 + S1 +S0 ) = not zero
GT = ( A > B ) = (A >= B) & NZ = greater than
LE = ( A <= B ) = (A > B) ' = ( A < B) | Zero = less or equal
Arquitectura de una Unidad Aritmética
Dispondremos de cuatro operaciones: and, or, suma,
resta y una instrucción de comparación.
Operandos de 32 bits, y condiciones para overflow.
Se decide emplear una operación de set on less, que
deje un uno en el bit menos significativo del resultado
si el operando A es menor que el operando B.
Puede plantearse un diseño modular. El siguiente
esquema, basado en multiplexores, logra cumplir las
especificaciones dadas.
Arquitectura de una Unidad Aritmética (cont)
Para una etapa cualquiera.
Si Binvert y CarryIn son unos, y la operación es suma,
se logra obtener la resta de A con B.
Arquitectura de una Unidad Aritmética (cont)
Etapa del bit más significativo.
ALU (cont)
Esquema general.
Arquitectura de una Unidad Aritmética (cont)
Modificación para tratar números con y sin signo.
slt usaría CLT=0
sltu usaría CLT=1
Análisis de un Sumador Binario
Para un sumador completo se tiene la siguiente tabla
de verdad:
Análisis de un Sumador Binario (cont)
Leyendo del mapa se obtienen, minimizando en dos
niveles:
Ci + 1 = Ai Bi + (Ai +Bi) Ci
Si = Ci’(AiBi’+Ai’Bi) + Ci( Ai’Bi’ +AiBi)
Como: (AiBi’+Ai’Bi) = Ai ⊕ Bi
Y su complemento es:
(Ai ⊕ Bi)’= (AiBi’+Ai’Bi)’ = (Ai’+Bi)(Ai+Bi’) = ( Ai’Bi’ +AiBi)
Se puede escribir en forma más compacta: Si = Ci ⊕ Ai ⊕ Bi
Análisis de un Sumador Binario (cont)
Empleando:
Gi = Ai Bi
Pi = Ai + Bi
Pueden escribirse como:
Ci+1 = Gi + Pi Ci
Si = Ci ⊕ ( Gi’ Pi)
El diagrama muestra que la suma binaria puede
realizarse mediante las señales Gi, Pi y Ci.
Esta forma se emplea en el diseño del sumador de
cuatro bits, con generación adelantada de la reserva,
74LS283.
Análisis de un Sumador Binario (cont)
Para efectuar un análisis más detallado de los retardos
combinacionales en un sumador se asumirá que la señal
Si se genera en dos niveles, a partir de Ai, Bi y Ci.
Y que la reserva de salida se genera empleando las
señales Gi, Pi y Ci, en tres niveles.
La organización de un sumador con propagación ondulada
de la reserva (ripple) produce las salidas con los
siguientes retardos de propagación medidos en unidades
de retardo a través de una compuerta:
Etapa:
i
i=2
i=1
i=0
Análisis de un Sumador Binario (cont)
Todos los tiempos se miden respecto al instante en
que están estables las entradas Ai, Bi y C0.
S0 se obtiene con retardo 2, C1 con retardo 3.
S1 se obtiene después de 5 unidades, C2 después de 6
unidades. Ya que desde las entradas A1, B1 y C1, C2 se
genera después de tres unidades, y S1 después de 2
unidades.
S2 se obtiene después de 8 unidades, C3 después de 9
unidades.
Si se obtiene después de 3*i +2 unidades, Ci+1 después de
3*i+3 unidades.
Si se hubieran generado las reservas y las sumas en
dos niveles, se tiene que tanto las suma como la
reserva de salida de la etapa i-ésima se obtienen en
2*i+2 retardos de propagación de una compuerta.
Para el caso de 32 bits se tendrán 64 retardos.
ALU: Generador de Reserva Adelantada
Se desea reducir el número de niveles para propagar
la reserva.
Se plantea un diseño modular agrupando 4
sumadores completos y generando las reservas (C1,
C2, C3 y C4) en dos niveles.
A continuación se desarrolla, en forma analítica, el
diseño lógico
ALU: Generador de Reserva Adelantada (cont)
En las ecuaciones de las reservas de los sumadores
completos se efectúan los siguientes reemplazos:
Gi = Ai Bi
Genera reserva de salida independiente de la reserva de
entrada. Si Gi es 1, entonces Ci+1 es uno (se genera reserva)
Pi = Ai + Bi
Propaga reserva de entrada hacia la reserva de salida. Si Pi es
0, no se propaga.
ALU: Generador de Reserva Adelantada (cont)
Se plantean las ecuaciones para las reservas en
función de Ai, Bi y Ci.
Luego se reemplaza la expresión para C1 en la
expresión para C2; a su vez ésta se reemplaza en la
expresión de C3, finalmente se reemplaza esta última
en la expresión para C4, resultan:
C1 = A0B0 +A0 C0 +B0C0 = G0 + C0 P0
C2 = A1B1 +A1 C1 +B1C1 = G1 + C1 P1 = G1 + (G0 + C0
P0) P1
C3 = A2B2 +A2 C2 +B2C2 = G2 + C2 P2 = G2 + (G1 +(G0 +
C0 P0) P1) P2
C4 = A3B3 +A3 C3 +B3C3 = G3 + C3 P3 = G3 + (G2 + (G1
+(G0 + C0 P0) P1) P2 )P3
ALU: Generador de Reserva Adelantada (cont)
Expresando en función de Gi, Pi y C0 se obtienen:
C1 = G0 + C0 P0
C2 = G1 + G0 P1 + C0 P0 P1
C3 = G2 + G1 P2 + G0 P1 P2 + C0 P0 P1 P2
C4 = G3 + G2 P3 + G1 P2 P3 + G0 P1 P2 P3 + C0 P0 P1 P2
P3 = G + C0 P
Se diseña un módulo que tenga como entradas Gi, Pi,
C0 y como salidas: C1, C2, C3, G y P.
Las ecuaciones anteriores se han integrado en una
sola pastilla (74182).
Notar que no se genera C4, sino G y P.
ALU: Generador de Reserva Adelantada (cont)
Diagrama
(
ALU: Generador de Reserva Adelantada (cont)
Respecto del instante en que se tienen estables las
entradas Ai, Bi y C0 se tienen, expresando en
unidades de retardo de propagación a través de una
compuerta:
S0 se obtiene después de 2 unidades.
P0 y G0 después de una unidad.
C1 después de 3 unidades.
S1 se obtiene después de 5 unidades (el tiempo de C1 más
los dos niveles del sumador).
P1 y G1 después de una unidad.
C2 después de 3 unidades (lo genera la unidad de adelanto).
ALU: Generador de Reserva Adelantada (cont)
Respecto del instante en que se tienen estables las
entradas Ai, Bi y C0 se tienen, expresando en
unidades de retardo de propagación a través de una
compuerta (cont):
S2 se obtiene después de 5 unidades.
P2 y G2 después de una unidad.
C3 después de 3 unidades.
S3 se obtiene después de 5 unidades.
P3 y G3 después de una unidad.
P se obtiene después de dos unidades y G se obtiene
después de 3 unidades.
C4 se obtiene después de 4 unidades, ya que se genera a
partir de G + C0P.
ALU: Generador de Reserva Adelantada (cont)
Un resumen del sumador de 4 bits con un nivel de
generación adelantada de las reservas, se muestra a
continuación:
ALU: Generador de Reserva Adelantada (cont)
Sumador de mayor orden
Una posibilidad de construir un sumador mayor es agrupar
bloques similares al anterior y propagar la reserva en forma
ondulada entre los sumadores completos de 4 bits:
ALU: Generador de Reserva Adelantada (cont)
Otra posibilidad es adelantar la reserva para los cuatro
grupos de sumadores de cuatro bits.
Esto consiste en generar a partir de C0 y las señales P y G
de cada sumador de 4 bits, las reservas C4, C8, C12 y C16,
mediante la red combinacional de generación de reservas
adelantadas.
Ejemplo: sumador de 16 bits con dos niveles de adelanto de
reserva
ALU: Generador de Reserva Adelantada (cont)
Diagrama:
Resumen de los
tiempos:
ALU: Generador de Reserva Adelantada (cont)
Si se forma un sumador de 32, con propagación
ondulada de la reserva entre los sumadores de 16
bits, se logra:
La solución anterior logra efectuar la suma en 16
retardos y la reserva de salida en 12.
Desplazador combinacional (shifter)
Las operaciones de corrimiento requieren una unidad
combinacional para efectuar los desplazamientos.
En corrimientos lógicos, a la izquierda o a la derecha se
rellenan con ceros las posiciones que se incorporan al
registro por la derecha o izquierda respectivamente.
En corrimientos aritméticos, sólo a la derecha, se rellenan
con el bit del signo las posiciones que se incorporan al
registro por la derecha.
Instrucciones MIPS de corrimiento inmediatos y variables:
shift left logical inmediato: sll $t1, $t2, 10 ; $t1 = $t2 << 10
shift right logical inmediato: srl $t1, $t2, 8
shift right arithmetic inmediato: sra $t1,$t2, 5
shift left logical variable: sllv $t1, $t2, $t3 ; $t1 = $t2 << $t3.
Desplazador combinacional (shifter) (cont)
A continuación se muestra un esquema, empleando mux
de dos vías, para desplazar hacia la derecha,
empleando redes combinacionales
A corresponde al operando de entrada, S al corrimiento
y R al resultado:
Desplazador combinacional (shifter) (cont)
Si los multiplexores son de 4 vías a uno, puede reducirse
el número de niveles y reducir el tiempo de propagación.
Se muestra una parte del primer nivel, y solo algunas
conexiones del segundo nivel.