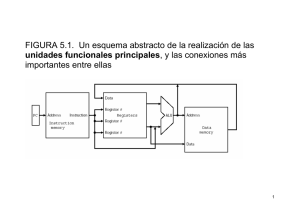
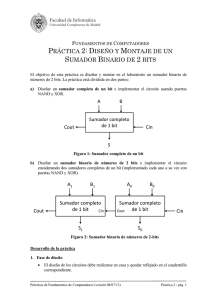
Práctica 4a - Universidad Autónoma de Madrid
Anuncio
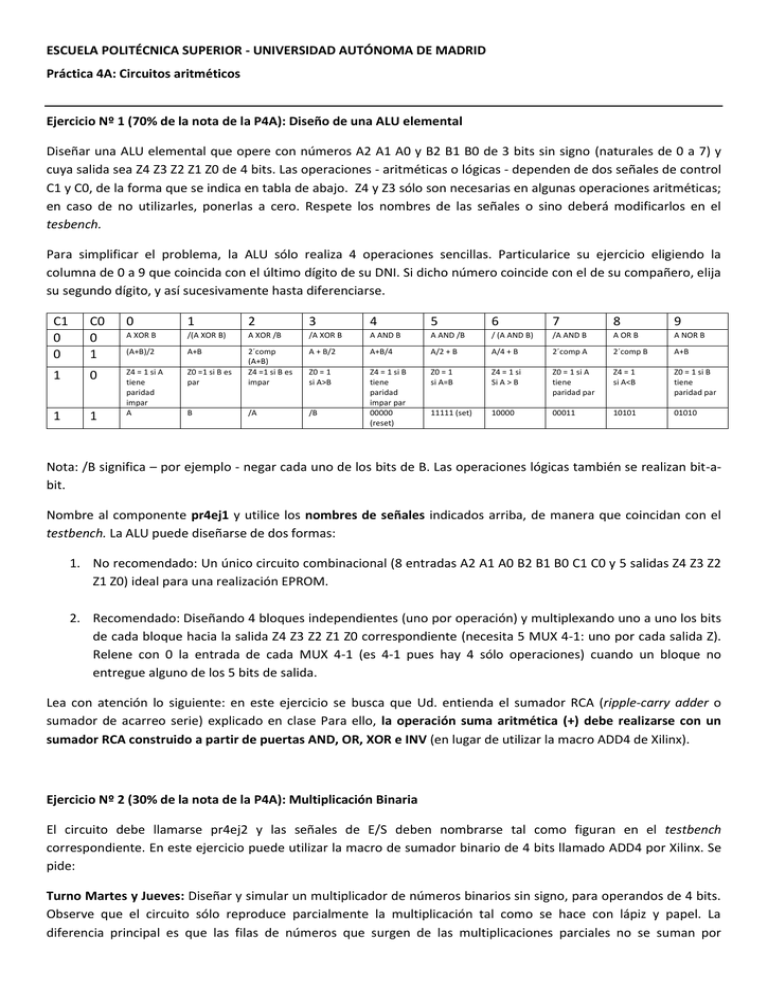
ESCUELA POLITÉCNICA SUPERIOR - UNIVERSIDAD AUTÓNOMA DE MADRID Práctica 4A: Circuitos aritméticos Ejercicio Nº 1 (70% de la nota de la P4A): Diseño de una ALU elemental Diseñar una ALU elemental que opere con números A2 A1 A0 y B2 B1 B0 de 3 bits sin signo (naturales de 0 a 7) y cuya salida sea Z4 Z3 Z2 Z1 Z0 de 4 bits. Las operaciones - aritméticas o lógicas - dependen de dos señales de control C1 y C0, de la forma que se indica en tabla de abajo. Z4 y Z3 sólo son necesarias en algunas operaciones aritméticas; en caso de no utilizarles, ponerlas a cero. Respete los nombres de las señales o sino deberá modificarlos en el tesbench. Para simplificar el problema, la ALU sólo realiza 4 operaciones sencillas. Particularice su ejercicio eligiendo la columna de 0 a 9 que coincida con el último dígito de su DNI. Si dicho número coincide con el de su compañero, elija su segundo dígito, y así sucesivamente hasta diferenciarse. C1 0 0 C0 0 1 0 1 2 3 4 5 6 7 8 9 A XOR B /(A XOR B) A XOR /B /A XOR B A AND B A AND /B / (A AND B) /A AND B A OR B A NOR B (A+B)/2 A+B A + B/2 A+B/4 A/2 + B A/4 + B 2´comp A 2´comp B A+B 1 0 Z0 =1 si B es par Z0 = 1 si A>B Z4 = 1 si Si A > B Z0 = 1 si A tiene paridad par Z4 = 1 si A<B Z0 = 1 si B tiene paridad par 1 B /A /B Z4 = 1 si B tiene paridad impar par 00000 (reset) Z0 = 1 si A=B 1 Z4 = 1 si A tiene paridad impar A 2´comp (A+B) Z4 =1 si B es impar 11111 (set) 10000 00011 10101 01010 Nota: /B significa – por ejemplo - negar cada uno de los bits de B. Las operaciones lógicas también se realizan bit-abit. Nombre al componente pr4ej1 y utilice los nombres de señales indicados arriba, de manera que coincidan con el testbench. La ALU puede diseñarse de dos formas: 1. No recomendado: Un único circuito combinacional (8 entradas A2 A1 A0 B2 B1 B0 C1 C0 y 5 salidas Z4 Z3 Z2 Z1 Z0) ideal para una realización EPROM. 2. Recomendado: Diseñando 4 bloques independientes (uno por operación) y multiplexando uno a uno los bits de cada bloque hacia la salida Z4 Z3 Z2 Z1 Z0 correspondiente (necesita 5 MUX 4-1: uno por cada salida Z). Relene con 0 la entrada de cada MUX 4-1 (es 4-1 pues hay 4 sólo operaciones) cuando un bloque no entregue alguno de los 5 bits de salida. Lea con atención lo siguiente: en este ejercicio se busca que Ud. entienda el sumador RCA (ripple-carry adder o sumador de acarreo serie) explicado en clase Para ello, la operación suma aritmética (+) debe realizarse con un sumador RCA construido a partir de puertas AND, OR, XOR e INV (en lugar de utilizar la macro ADD4 de Xilinx). Ejercicio Nº 2 (30% de la nota de la P4A): Multiplicación Binaria El circuito debe llamarse pr4ej2 y las señales de E/S deben nombrarse tal como figuran en el testbench correspondiente. En este ejercicio puede utilizar la macro de sumador binario de 4 bits llamado ADD4 por Xilinx. Se pide: Turno Martes y Jueves: Diseñar y simular un multiplicador de números binarios sin signo, para operandos de 4 bits. Observe que el circuito sólo reproduce parcialmente la multiplicación tal como se hace con lápiz y papel. La diferencia principal es que las filas de números que surgen de las multiplicaciones parciales no se suman por columnas (como se hace con lápiz y papel) sino que se suman las dos primeras filas y al resultado de esta operación se le suma la tercera fila y así sucesivamente. Turnos Viernes: Diseñar y simular un multiplicador de números binarios en complemento a 2, para operandos de 4 bits (utilice el algoritmo Baugh & Wooley). El algoritmo de Baugh-Wooley permite multiplicar números en complemento a 2, utilizando una estructura muy similar al esquema explicado en las clases de teoría. En las figuras adjuntas se resumen las principales modificaciones a realizar sobre el multiplicador unsigned, que consisten en: a) negar algunos productos parciales; es decir cambiar AND por NAND y b) agregar una fila adicional (y un sumador extra) con los dígitos 10010 (para 4 bits). Figura 1: Multiplicación binaria sin signo siguiendo un esquema parecido a “lápiz y papel” Figura 2: Modificación de Baugh-Wooley para operar en complemento a 2. Deben cambiarse algunas AND por NAND y agregar la suma de 1001. Es decir, en vez de salir en la Fig.1 con P7 P6 P5 P4 directamente, llevarlos a un cuarto sumador y sumarle 1001.