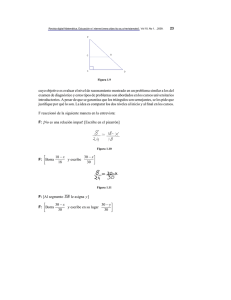
E( ¯g)|ds ≤ ∫ t 0 [a2M|| ¯G − ¯g|| ∫R3×S2 B(η, w − v)ξ(s, x, v 0
Anuncio

Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol 8, No 1. , 2007. 13 ahora Z t 0 | E( Ḡ ) − E( ḡ)|ds ≤ + + Z t 0 Z t 0 Z t 0 a2 M|| Ḡ − ḡ|| a2 K || Ḡ − ḡ|| Z Z a2 M|| Ḡ − ḡ|| R3 ×S2+ Z ′ ′ B(η, w − v)ξ (s, x, v )ξ (t, x + aη, w )|dwdη ds R3 ×S2+ ′ ′ B(η, w − v)ξ (t, x, v )ξ (t, x + aη, w )|dwdη ds R3 ×S2+ ′ ′ B(η, w − v)ξ (t, x, v )ξ (t, x + aη, w )|dwdη ds Z t Z + a2 ξ (s, x, v) M|| Ḡ − ḡ|| 0 + + Z t 0 Z t 0 a2 ξ (s, x, v) M|| ḡ − Ḡ || a2 ξ (s, x, v)K || ḡ − Ḡ || Z Z R3 ×S2+ R3 ×S2+ R3 ×S2+ B(η, w − v)ξ (t, x − aη, w)dwdη ds B(η, w − v)ξ (t, x − aη, w)dwdη ds B(η, w − v)ξ (t, x − aη, w)dwdη ds. como B(η, w − v) ∈ L1loc (R3 × S2+ ) y ξ (t, x ± aη, w) ∈ L∞ (R3 × S2+ ) entonces por ′ desigualdad de Hölder tenemos la existencia de L, L tal que: Z R3 ×S2 B(η, w − v)ξ (s, x ± aη, w)dwdη < L + Z ′ ′ ′ R3 ×S2 B(η, w − v)ξ (t, x, v )ξ (s, x ± aη, w )dwdη < L + entonces || Ḡ# − ḡ# || ≤ 1 ξ (s, x, v) Z t 0 ′ ′ ′ ( a2 ML + a2 KL + a2 ML + a2 ξ (t, x, v) ML + a2 ξ (t, x, v) ML)|| Ḡ − ḡ|| dt. y por la desigualdad de Gronwall tenemos que Ḡ = ḡ es una solución distribucional de la ecuación de Enskog (1)