Descargar ejercicio en PDF
Anuncio

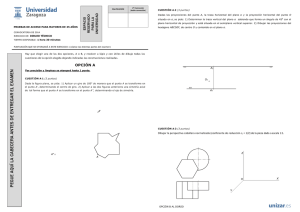
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
SOLUCIÓN
1. Sitúa los puntos
Mide la primera coordenada (X) en la dirección de la Línea de Tierra, empezando desde la
izquierda
La segunda coordenada (Y) en perpendicular a la LT, con las positivas hacia abajo
La tercera coordenada (Z) en perpendicular a la LT, con las positivas hacia arriba.
2. Halla las trazas del plano α
Encuentra los puntos traza h y v' de algunas de las rectas que forman los tres puntos, por
ejemplo de la recta 1-3 o de la recta 1-2.
Une los puntos traza para obtener el plano
3. Coloca el lado AB del hexágono
El punto A pertenece al plano α y al vertical. Por tanto pertenece a la traza vertical α' del
plano. Puesto que está a 65 mm del plano horizontal, colócalo a 65 mm de la LT.
El lado AB es horizontal, por lo que su proyección vertical es paralela a LT y su proyección
horizontal paralela a la traza horizontal α del plano. Los 40 mm del lado los puedes medir
directamente en la proyección horizontal, que se ve en verdadera magnitud
4. Abate el plano y el lado AB
Abate el punto A. Con centro en la intersección de las trazas y radio hasta a' dibuja un arco
de circunferencia. Desde a dibuja una perpendicular a la traza horizontal α del plano que
cortará al arco anterior en (A) abatido.
El lado AB es horizontal, por lo que su abatimiento es paralelo a la traza horizontal del α
plano.
5. Dibuja el hexágono en el abatimiento
En el hexágono, el lado es igual al radio. Dibuja desde (A) y (B) dos arcos de circunferencia
con radio (A)-(B) que determinarán el centro (O) de la circunferencia circunscrita al hexágono. (D) y (E) están en las diagonales que pasan por (A) y (B) respectivamente.
Por (O) dibuja una paralela a (A)-(B) que cortará a la circunferencia en (C) y (F)
6. Desabate el hexágono
Puedes desabatir cada recta o hacerlo por afinidad, como he hecho yo. La recta (A)-(O) es
afín la recta a-o y tienen un punto doble en la traza del plano. Igual ocurre con la diagonal
(B)-(E).
Pasa por la proyección horizontal o del centro una recta paralela a la traza, en la que se
encuentran c y f.
7. Encuentra las proyecciones verticales
Las rectas C-F y D-E son horizontales de plano y sus proyecciones verticales son, por tanto,
paralelas a la LT
1
SITÚA LOS PUNTOS
M
ide las coordenadas de cada punto
desde O
X
positivo del punto 3
Z
positivo del punto 3
Y
positivo del punto 3
Z
X
Y
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
2
HALLA LAS TRAZAS DEL PLANO
h1 y v1’
son los puntos traza
de la recta 1-2
h3
es el punto
traza horizontal
de la recta 2-3
U
ne los puntos traza
para obtener las trazas
del plano
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
3
COLOCA EL LADO AB DEL HEXÁGONO
65
mm es la cota
de la recta AB, que es
horizontal de plano
L
a proyección
horizontal de una
recta horizontal es
paralela a la traza
horizontal del
plano
V
erdadera Magnitud en la
proyección horizontal de la
recta. Mide ahí los 40 mm
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
4
ABATE EL PLANO Y EL LADO AB
A
bate a’, porque
pertenece a la traza
vertical
P
erpendicular
desde la proyección horizontal
L
ado AB abatido,
paralelo a la traza
horizontal del plano
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
5
DIBUJA EL HEXÁGONO EN EL ABATIMIENTO
E
n el hexágono, el lado es
igual al radio de
la circunferencia
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
6
DESABATE EL HEXÁGONO
P
erpendicular a
la traza horizontal
del plano
D
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm esabatimiento
estando (A) enpor
el plano
Homología
Afín de (A)
vertical de proyección a 65 mm por encima del plano horizontal (B)
a la izquierda
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
7
ENCUENTRA LA PROYECCIÓN VERTICAL
P
royección
vertical paralela a LT
L
as rectas
C-F y D-E son
horizontales
de plano
Determinar la proyección diédrica de un hexágono regular (A, B, C, D, E, F) contenido en el
plano (alpha) sabiendo que el lado (A-B) es horizontal y mide 40 mm estando (A) en el plano
vertical de proyección a 65 mm por encima del plano horizontal (B) a la izquierda de (A)
Puntos:(alpha) {1(30,70,22), 2(55,20,67), 3(100,15,33)}
¡¡Hasta el próximo artículo!!
Visita http://www.10endibujo.com/
=)