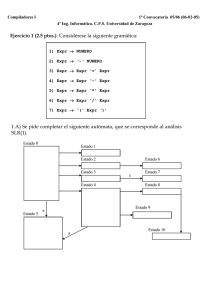
resumen de maxima
Anuncio

RESUMEN DE MAXIMA
OPERADORES
Tipos de operadores
Prefijo (prefix).- Son unarios con un único operando que se escribe a continuación del operador.
Ejemplos: - , not.
Sufijo (postfix).- Son unarios con un único operando que se escribe antes del operador. Ejemplo: !.
Infijo (infix).- Son binarios y se colocan entre dos operandos. Ejemplo : ^, :.
N-ario (n-ary).- Tienen un número arbitrario de operandos. Ejemplo: * y +.
Acotador (matchfix).- Se utilizan para establecer el comienzo y final de una lista de operandos.
Los corchetes son ejemplos de acotadores, que se utilizan para definir una lista tal como [a, b, ...].
No-fijo (nofix).- Carece de operandos.
Operadores
Aritméticos
Relacionales
+
*
/
^
**
^^
.
<
<=
>
>=
Suma
Resta
Producto
División
Potencia
Potencia
Potencia no conmutativa
Producto de matrices
Lógicos Para ecuaciones y asignaciones
Menor
not No
Menor o igual and Y
Mayor
or O
Mayor o igual
#
=
:
::
:=
::=
Distinto
Igual
Asignación
Asignación
Definir
Definir
Podemos
definir
nuestros
propios
operadores, y con las funciones remove y
kill podemos eliminar las propiedades del los
operadores o eliminarlos.
La llamada remove ("s+", op) sólo elimina las
propiedades de operador s+ de a, mientras que
la llamada kill ("s+") elimina todas las
propiedades de a, incluidas las propiedades de
operador.
Podemos controlar la evaluación de símbolos, funciones
y expresiones algebraicas mediante una comilla simple
(') o dos comillas simples (''). Mientras que con una
comilla simple se suprime la evaluación, con dos
comillas simples se evalúa.
•
•
•
•
•
•
•
•
Si escribimos: ev (expr, arg_1, …, arg_n) se evalúa una expresión (expr) utilizando los argumentos
(arg_1,..., arg_n). Siendo, algunos de los argumentos los siguientes:
simp.- Simplifica la expr sin importar el valor de la variable
noeval.- Suprime la fase de evaluación de ev
nouns.- Evalúa las formas nominales.
expand.- Expande exp.
diff.- Realiza todas las derivadas indicadas en expr.
float.- Convierte los números racionales (no-enteros) a números decimales de coma flotante.
numer.- Se evalúa exp como punto flotante si no contiene la expresión variables.
V: expresion.- Le asigna a V el valor de expresión
Operadores de asignación
;
evalúa la expresión y devuelve el resultado. Ejemplo: 1+ sqrt(2/3);
$
evalúa una expresión sin devolver el resultado. Ejemplo: b: sqrt(3)$
%
evalúa el último cálculo efectuado
? comando muestra ayuda sobre lo que hace referencia el comando.
:
asigna a una variable escrita a la izquierda el valor escrito a la derecha
example(comando) muestra ejemplos del comando
kill(variable o función) borra variable o función
kill(all) reinicia el sistema
Constantes
%pi es el número pi = 3,14159...
true
es el valor lógico “verdadero”
%e
es el número e = 2,7183...
false
es el valor lógico “falso”
%i
es la unidad imaginaria i = sqrt(-1)
inf
es +infinito
minf
es -infinito
Expresiones
Funciones habituales de números reales
Valores aproximados a números reales
abs(x)
floor(x)
round(x)
sqrt(x)
exp(x)
log(x)
valor absoluto de x
parte entera de x
redondeo entero de x
raiz cuadrada de x
e elevado a x
logaritmo neperiano de x
float(x) es el valor decimal aproximado de x
bfloat(x) es el valor aproximado de x en
notación científica
fpprec:n fija la aproximación dada por bfloat a
n cifras (por defecto es 16)
Trigonometría
Aritmética entera (también para polinomios)
F. trigonométricas: sin(x), cos(x), tan(x)
F. trigonométricas inversas: asin(x), acos(x),
atan(x)
trigexpand(a) desarrolla
la
expresión
trigonométrica a utilizando las fórmulas de la
suma de seno y coseno
trigreduce(a) reduce
un
polinomio
trigonométrico a.
trigsimp(a)
simplifica
la
expresión
trigonométrica
a
usando
la
relación
2
2
cos t+sin t=1 , y sustituyendo tan t por
sin t
cos t
load(ntrig)
carga el paquete, lo que permite
obtener los valores exactos de sin x, cos x y tan x
cuando x es un múltiplo de π
10
divide(a,b) división euclídea de a por b.
divisors(a) conjunto de divisores de a
divsum(a)
suma de los divisores de a
mod(a,b)
resto de división de a entre b
gcd(a,b) M.C.D. de los números enteros a y b
lcm(a,b) M.C.M. de los números enteros a y b
primep(p)
verifica si el natural p es primo
prev_prime(n) mayor primo menor n
next_prime(n) menor primo mayor que n
factor(n)
descomposición del natural n en
producto de factores primos
ifactors(n) descomposición de n en producto
de factores primos
binomial(n,p) es el número binomial n sobre p
random(n) número natural, elegido al azar
entre 0 y n - 1
Números complejos
Límites, tangentes y asíntotas
realport(z)
imagport(z)
conjugate(z)
abs(z)
carg(z)
rectform(z)
polarform(z)
limit(f(x)/x,x,0) límite de f(x) en x = 0
limit(f(x),x,0,plus) límite de f(x) en x = 0 por la
derecha
limit(f(x),x,0,minus) límite de f(x) en x = 0 por
la izquierda
limit(f(x),x,inf) límite de f(x) en x = + infinito
limit(f(x),x,minf) límite de f(x) en x = - infinito
taylor(f(x),x,a,n) desarrollo de Taylor de f
respecto de x en el punto a con n términos
es la parte real de z
es la parte imaginaria de z
es el conjugado de z
es el módulo de z
es el argumento de z (en (-pi,pi])
es la forma cartesiana de z
es la forma polar de z
Cálculo algebraico
Funciones: Derivación,
integración
representación
e
R:x^4-4*x^2-5 polinomio R= x 4−4∗x 2−5
expand(P)
desarrolla P
factor(P)
factoriza P en R
gfactor(P)
factoriza P en C
solve(P,x)
raices complejas de P
subst(4,x,P) valor de P cuando x = 4
ratcoef(P,x^3) es el coeficiente del término en
3
x de P
divide(P,Q,x) es la lista formada por el cociente
y el resto de la división de P por Q.
portfrac(P/Q,x) descompone la función racional
P/Q en elementos simples
ratsimp(expr) simplifica la expresión racional
expr (reduce a común denominador)
subst(1/z,x,expr) sustituye x por 1/z en la
expresión expr
subst (a, b, P) Sustituye a por b en expresión P
f(x):=x^2-1
Define
define(f(x),x x^2-1) Define
f:lambda([x],x^2-1) Define
Ecuaciones
Sistemas de ecuaciones
solve(P(x)=Q(x),x)
resolución exacta
en C, de la ecuación P(x) = Q(x)
find_root(P(x)=Q(x),x,a,b) solución
aproximada en [a,b], de la ecuación P(x) = Q(x)
allroots(P(x)=Q(x))
valores
aproximados de todas las soluciones (reales y
complejas), de la ecuación P(x) = Q(x)
linsolve([ecuación 1, ecuación 2, … , ecuación
k], [variable 1, variable 2, … , variable k])
Resuelve el sistema de lineal de k ecuaciones
algsys(([ecuación 1, ecuación 2, … , ecuación
k], [variable 1, variable 2, … , variable k])
Resuelve el sistema no lineal de k ecuaciones
f ( x )=x 2−1
f ( x )=x 2−1
f ( x )=x 2−1
diff(f(x),x)
es la derivada de f ( x)
diff(f(x),x,2) es la derivada segunda f (x)
define(g(x),diff(f(x),x)) define g(x)=f ' (x)
taylor(f(x),x,a,1) es la ecuación reducida de la
tangente a f en el punto (a , f (a))
plot2d([f(x),g(x)],[x,x1,x2],[y,y1,y2])
representa las funciones f y g en la región
[x 1, x 2] x [ y 1, y 2 ]
integrate(f(x),x)
primitiva de f(x)
integrate(f(x),x,a,b) integral definida de f(x)
entre a y b
romberg(f(x),x,a,b) es una aproximación de
la integral definida de f(x) entre a y b
Listas
L:makelist(k^2,k,0,15) Lista L con los cuadrados de los 15 primeros naturales
L[2]:5
sustituye segundo elemento de L por 5
length(L)
longitud de la lista L.
first(L)
primer elemento de L
second(L)
segundo elemento de L
last(L)
último elemento de L
member(x,L)
se verifica si x pertenece a L
append(L1,L2) concatena las listas L1 y L2
join(L,M)
construye una lista, intercalando los elementos de L y M.
sort(L)
ordenación de los elementos de L en orden creciente.
map(f,L)
aplicación de la función f a todos los elementos de L
Sumas y productos
Matrices
sum(1/k^3,k,1,10)
es la suma de los
inversos de los cubos de los enteros entre 1 y 10.
product(1/k^3,k,1,10) es el producto de los
inversos de los cubos de los enteros entre 1 y 10.
load(simplify_sum) $ sum(1/k^3,k,1,inf) $
simplify_sum(%)
calcula la suma de los
inversos de los cubos de los enteros entre 1 y +
infinito.
A:matrix([9,8,7],[6,5,4],[3,2,1])
define
matriz la matriz A = ([9,8,7],[6,5,4],[3,2,1])
B:genmatrix(lambda([i,j],i+j),3,2) genera la
matriz B = ([2,3],[3,4],[4,5])
zeromatrix(m,n) matriz nula de orden m x n
ident(n)
matriz identidad de orden n.
diag_matrix(a,b,c) matriz diagonal ([a,0,0],
[0,b,0],[0,])
Programación
Operaciones con matrices
nombre(parámetros
de
entrada):= A+B
suma de las matrices A y B
block([variables locales], <instrucción 1>, .... k*A
producto de la matriz A por k
<instrucción n>, /* -------Comentario------ */) A.B
producto de las matrices A y B
Ejemplo.- suma(a,b) := block([c],c:a+b, A^^n
matriz A elevada a n
return(c))
invert(A)
inversa de la matriz A
ESTRUCTURA CONDICIONAL
transpose(A)
traspuesta de la matriz A
if
(condición)
then
(<instrucción1>, determinant(A) determinante de A
<instrucción2>)
else
(<instrucción3>, rank(A)
rango de matriz A
<instrucción4>)
ident(n)
matriz identidad de orden n
ESTRUCTURAS ITERATIVAS
Bucle For (tabla del 7).- for k from 1 thru 10
do (print("7 veces",k,"igual a",7*k))
Bucle While para escribir la tabla del 7.- k:1 $
while k<11 do (print("7 veces",k,"igual
a",7*k), k:k+1)
Formatos gráficos de Maxima
• gnuplot
(formato por defecto para Windows)
• gnuplot_pipes
(formato por defecto para plataformas distintas de Windows)
• mgnuplot
(interfaz para Gnuplot basada en Tk)
• xmaxima
(interfaz gráfico Tcl/Tk de Maxima)
Funciones y variables para gráficos
contour_plot (expr(x,y), [x,a,b], [y,c,d], options, …) - solo funciona con gnuplot o gnuplot_pipes
Dibuja curvas de nivel de expr(x) en el rectángulo [a,b]x[c,d], utilizando las opciones options
plot2d(expr(x), [x,a,b], [y,c,d], options, …)
Gráfica de expr(x) en el rectángulo [a,b]x[c,d], utilizando las opciones options
plot2d([expr1(x),...,exprn(x)], [x,a,b], [y,c,d], options, …)
Gráfica de expr1(x), …, exprn(x) en el rectángulo [a,b]x[c,d], utilizando las opciones options
Ejemplos:
(%i1) plot2d (sin(x), [x, -%pi, %pi])$
Si la función crece rápidamente puede ser necesario
limitar los valores del eje vertical:
(%i1) plot2d (sec(x), [x, -2, 2], [y, -20, 20])$
plot2d: some values were clipped.
Gráfico con escala logarítmica:
(%i1) plot2d (exp(3*s), [s, -2, 2], [logy])$
Ejemplo de función paramétrica. Curva de la mariposa:
(%i1) r: (exp(cos(t))-2*cos(4*t)-sin(t/12)^5)$
(%i2) plot2d([parametric, r*sin(t), r*cos(t),[t, -8*%pi, 8*
%pi], [nticks, 2000]])$
(%i1) plot2d([[parametric, cos(t), sin(t),[t,0,2*%pi], (%i1) plot2d ([discrete,
[nticks, 80]],[abs(x)], [x,-2,2], [y, -1.5, 1.5])$
[.6, .9, 1.1, 1.3, 1.4]])$
plot2d: some values were clipped.
[10,
20,
30,
40,
50],
(%i1) plot2d([discrete, [[10, .6], [20, .9], [30, 1.1],[40, (%i1) xy: [[10, .6],[20, .9],[30, 1.1], [40, 1.3], [50, 1.4]]$
1.3], [50, 1.4]]],[style, points])$
(%i2) plot2d([[discrete, xy], 2*%pi*sqrt(l/980)], [l,0,50],
[style, points, lines], [color, red, blue],[point_type,
asterisk],[legend,
"experiment",
"theory"],[xlabel,
"pendulum's length (cm)"], [ylabel, "period (s)"])$
plot3d(expr(x,y), [x,a,b], [y,c,d],[z,e,f], options, …)
Gráfica de expr(x,y) en el rectángulo [a,b]x[c,d]x[e,f], utilizando las opciones options
plot3d([expr1(x),...,exprn(x)], [x,a,b], [y,c,d], options, …)
Gráfica de expr1(x), …, exprn(x,y) en el ortoedro [a,b]x[c,d]x[e,f], utilizando las opciones options
Ejemplos:
(%i1) plot3d (2^(-u^2 + v^2), [u, -3, 3], [v, -2, 2])$
(%i1) expr_1:5*cos(x)*(cos(x/2)* cos(y)+ sin(x/2)*sin(2*y) +3.0)-10.0$
(%i2) expr_2:-5*sin(x)*(cos(x/2)*cos(y) + sin(x/2)*sin(2*y) + 3.0)$
(%i3) expr_3: 5*(-sin(x/2)*cos(y) + cos(x/2)*sin(2*y))$
(%i4) plot3d ([expr_1, expr_2, expr_3], [x, -%pi, %pi],[y, -%pi, %pi],
[grid, 40, 40])$
Algunas opciones para gráficos
axes [axes, true]
Dibuja ejes
axes [axes, true]
Oculta ejes
color [color,color_1,…,color_n] Define colores. Por defecto: blue,red,green,magenta,black,cyan
legend [legend, string_1, …, string_n]
Define títulos
logx [logx] Escala logarítmica en eje OX
logy [logy] Escala logarítmica en eje OX
point_type [point_type, type_1, …, type_n] Tipos de puntos. Por defecto: bullet, circle, plus, times,
asterisk, box, square, triangle, delta, wedge, nabla, diamond, lozenge
style [style, type_1, …, type1_n]
Tipo de linea: lines, points, linespoints, dots, impulses.
x [x, min, max]
Valor mínimo y máximo de eje OX , … ,
z [z, min, max]
Valor mínimo y máximo de eje OZ
xlabel [xlabel, título1]
Título1 para eje OX, … ,
zlabel [xlabel, título3]
Título3 para eje OZ
Polinomios En mayoría de los casos se puede indicar variables ,x,y
algebraic
Por defecto: false. Debe valer: true, para simplificación de enteros algebraicos.
coeff (expr(x), x, n) Devuelve el coeficiente de x^n en expr(x) – (la ordén no expande expr(x))
divide (P, Q,x)
Cociente y el resto de división de P entre Q, de variable principal x.
factor (expr)
Factoriza la expresión expr
gcd (P1,...,Pn)
Máximo común divisor de P1,..., y Pn.
ratsimp (expr)
Simplificación racional de expr.
Programación
SINTAXIS
nombre(parámetros de entrada) := block([variables locales],<instrucción 1>,....,<instrucción n>,
/* -------Comentario------ */)
Ejemplo simple:
suma(a,b) := block([c], c:a+b, return(c))
ESTRUCTURA CONDICIONAL
if (condición)
then (<instrucción1> , <instrucción2>)
else (<instrucción3> , <instrucción4>)
ESTRUCTURAS ITERATIVAS
Bucle For para escribir la tabla del 7:
for k from 1 thru 10 do (print("7 veces",k,"igual a",7*k))
Bucle While para escribir la tabla del 7:
k:1 $ while k<11 do (print("7 veces",k,"igual a",7*k), k:k+1)