Difusión en Químicax
Anuncio
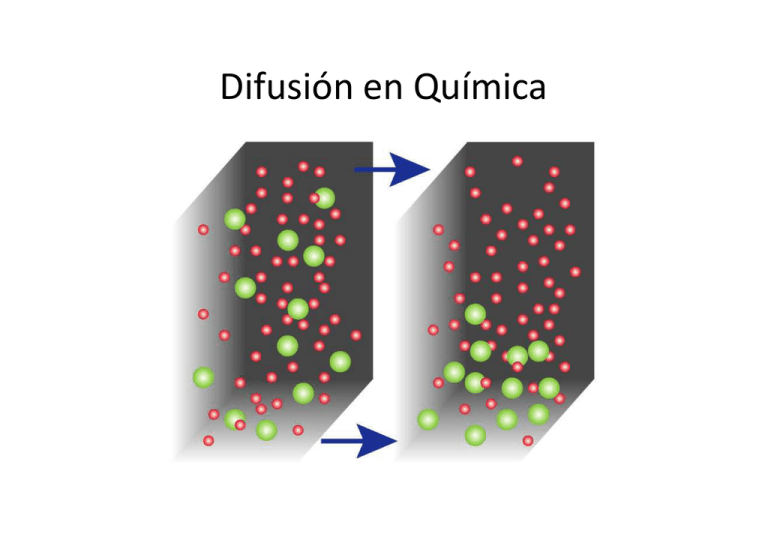
Difusión en Química Concepto de difusión. Leyes de Fick Concepto de difusión. Leyes de Fick • fuerza impulsora sólo existe cambio en una coordenada Difusión. Primera ley de Fick • Flujo de soluto, J, se define como la velocidad de transporte de moles de soluto, n, a través de una superficie de área unidad, A, situado en una posición x. Coeficiente Difusión, D El signo menos indica que la difusión tiende a anular el gradiente A medida que se va produciendo el proceso de difusión, el gradiente (fuerza impulsora) va cambiando con el tiempo y por tanto el flujo se irá haciendo más lento. Difusión • Vamos a estudiar su variación a través de una coordenada • Derivaremos J con respecto a x Según elemento diferencial de volumen Por ser variables independientes Difusión. Segunda Ley de Fick • Como y teniendo en cuenta Esta ecuación indica que el cambio de concentración en un punto x es proporcional a la curvatura del perfil de concentraciones c(x,t) respecto a la posición Como toda ecuación diferencial, para obtener la solución de la segunda Ley de Fick, es preciso establecer condiciones de contorno adecuadas al sistema estudiado Segunda Ley de Fick vesícula sináptica +célula nerviosa =liberación de transmisores c c Figura a x c Figura b x Figura c x flujo está dirigido hacia fuera n o hay flujo neto flujo constante La curva va ensanchándose y disminuyendo en altura en el transcurso del tiempo Primer caso de interés en Química c(x, t=0)= c0 para x<0 y c(x,t=0)=0 para x>0. X<0 erf(y), función de error X=0 X>0 Segunda situación de interés en Química • c(x,t=0)= c0 δ(x-x0) x0 donde δ(x-x0) es la función delta de kronecker Corresponde a un sistema que inicialmente tiene una concentración c0 (para x=x0 y a partir de ahí el soluto se difunde hacia La solución de la segunda Ley de Fick Esta función corresponde a una curva simétrica en x que tiene valores pequeños cuanto mayor es x. • La constante de proporcionalidad se puede evaluar si se estipula la cantidad total del cuerpo que se difunde por unidad de superficie. Supongamos que es c0. función gaussiana que se ensancha a medida que crece t Como función de probabilidad • Esta función nos informa de cómo están distribuidas las moléculas en el sistema para un valor determinado del tiempo. De aquí que podamos considerarla como una función de probabilidad. Relación entre distancia cuadrática media y coeficiente de difusión Einstein-Smoluchowski movimiento browniano Determinación del coeficiente de Difusión. • En gases • Teoría cinética. Coeficiente difusión (D) Distancia recorrida (cm) en 60 s Gases ≈ 10-1 3 Líquidos ≈10-5 0.03 Sólidos ≈10-20 < 10-8 Determinación del coeficiente de Difusión Medios condensados Medir coeficientes de algunos coloides, simplemente midiendo con un microscopio los desplazamientos La altura de la campana,H, (x=0) viene dado por Determinación del coeficiente de Difusión • El área ba jo la curva es c0 Combinando estas dos últimas ecuaciones Representando graficamente (A/H)2 frente a t obtendremos una recta de pendiente 4πD También se puede utilizar la primera ley de Fick J = flujo con unidades de mol cm-2 s-1 c2,c1= concentraciones mol cm-3 Δx = anchura del disco D = coeficiente de difusión cm2 s-1 Métodos ópticos para medir la variación de la concentración con el tiempo en un determinado punto de la muestra. Métodos ópticos Métodos ópticos para medir la variación de la concentración con el tiempo en un determinado punto de la muestra. •Radiactividad •Absorción •Fluorescencia •Índice de refracción Einstein-Sutherland f es el coeficiente de fricción difusión: relación entre un término KT que promueve el movimiento y el término f que se opone a éste. Efecto de la forma esfera perfecta de radio r Coeficientes de fricción. Factores de Perrin f 0 • Para formas especiales de partículas no esféricas a/b= ½ f/f0=1.042 a/b= 2 f/f0=1.044 a/b = 1/10 f/f0=1.458 a/b = 10 f/f0=1.543 Efecto de solvatación • radio hidrodinámico coraza de solvatación (core-shell). Coeficientes de difusión en diferentes medios a 25ºC, D/10-9 m2s-1 Compuesto Disolvente D Compuesto Disolvente D Iodo hexano 4.05 Hemoglobina Agua 0.070 Iodo Cl4C 3.42 Seoalbumina Agua 0.067 Iodo benceno 2.13 Lisozima Agua 0.115 Glicina Agua 1.06 Ribonucleasa Agua 0.131 Glucosa Agua 0.68 Mioglobina Agua 0.113 Efecto de la temperatura • coeficientes de difusión • deben aumentar al • subir la temperatura Superar esta barrera de fricción debe llevar a una variación exponencial de D TRANSPORTE BAJO FUERZAS CENTRÍFUGAS. SEDIMENTACIÓN. Tres la fuerzas que actúan sobre la partícula: Fuerza de fricción : Fr= -f vx (f coeficiente de fricción y vx velocidad) Fuerza de gravitación: F= m g Fuerza ascensional: Fasc= -m Veρg (Ve es el volumen específico del soluto y ρ densidad del medio) . ultracentrifugación • La partícula alcanzará una velocidad constante, ese momento ocurre cuando las fuerzas de fricción y ascensional quedan balanceadas por la fuerza gravitacional. 0= -f vx + m g -m Veρg vx/g= S coeficiente de sedimentación, S La sedimentación no se utiliza usando la fuerza gravitatoria. En su lugar, la sedimentación se consigue usando una centrífuga que se mueve con una velocidad angular ω. Velocidad frontera de sedimentación • Campos centrífugos≈ 105 g • • Con estas aceleraciones cualquier macromolécula sedimenta En este caso sustituimos g por ω2r Si D=kT/f •Medida: • volumen específico •coeficiente de difusión •coeficiente de sedimentación Método de equilibrio de sedimentación • Se utilizan bajas velocidades de rotación • Tras varias horas, a veces días, de centrifugación se llega a un equilibrio entre la sedimentación que tiende a llevar partículas hacia el fondo y la difusión que tiende a homogeneizar la disolución. En estas condiciones no hay flujo neto de materia, J=0. La condición de equilibrio es que el potencial total, sea constante en todas partes El potencial total se define como la suma del potencial químico y la energía potencial (U(r)) originada por la fuerza centrífuga ala que se somete la muestra Método de equilibrio de sedimentación • En el equilibrio No hay que olvidar el empuje del principio de Arquímedes Método de equilibrio de sedimentación • integración entre el menisco (a) y algún punto r ¿Cómo obtener S? t vs integramos pendiente Revoluciones por segundo