Introducción a las Funciones Vectoriales (Funciones de R

Introducción a las Funciones Vectoriales (Funciones de R → Rn )
1
Torsión
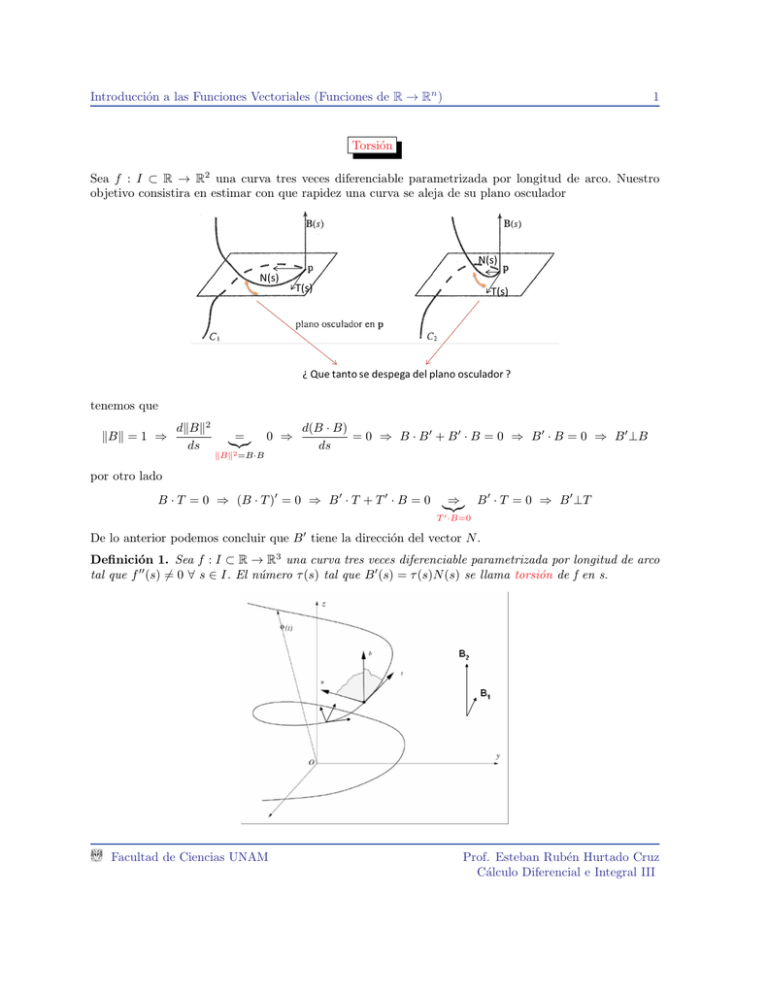
Sea f : I ⊂ R → R2 una curva tres veces diferenciable parametrizada por longitud de arco. Nuestro
objetivo consistira en estimar con que rapidez una curva se aleja de su plano osculador
tenemos que
kBk = 1 ⇒
dkBk2
ds
=
|{z}
0 ⇒
kBk2 =B·B
d(B · B)
= 0 ⇒ B · B 0 + B 0 · B = 0 ⇒ B 0 · B = 0 ⇒ B 0 ⊥B
ds
por otro lado
B · T = 0 ⇒ (B · T )0 = 0 ⇒ B 0 · T + T 0 · B = 0 |{z}
⇒ B 0 · T = 0 ⇒ B 0 ⊥T
T 0 ·B=0
De lo anterior podemos concluir que B 0 tiene la dirección del vector N .
Definición 1. Sea f : I ⊂ R → R3 una curva tres veces diferenciable parametrizada por longitud de arco
tal que f 00 (s) 6= 0 ∀ s ∈ I. El número τ (s) tal que B 0 (s) = τ (s)N (s) se llama torsión de f en s.
Facultad de Ciencias UNAM
Prof. Esteban Rubén Hurtado Cruz
Cálculo Diferencial e Integral III
Introducción a las Funciones Vectoriales (Funciones de R → Rn )
2
En la figura anterior vemos que la torsión representa una variación en la dirección del vector binormal,
procederemos ahora a desarrollar una fórmula para calcularla
Tenemos que
T (s) = f 0 (s)
ahora bien
N (s) =
f 00 (s)
kf 00 (s)k
por lo tanto
kf 00 (s)kf 000 (s) − f 00 (s)
0
N (s) =
f 00 (s)·f 000 (s)
kf 00 (s)k
kf 00 (s)k2
f 000 (s)
= 00
− f 00 (s)
kf (s)k
f 00 (s) · f 000 (s)
kf 00 (s)k3
Luego entonces si
B 0 (s) = T (s) × N 0 (s)
se tiene que
B 0 (s) = f 0 (s)×
f 000 (s)
−f 00 (s)
kf 00 (s)k
f 00 (s) · f 000 (s)
kf 00 (s)k3
=
00
f (s) · f 000 (s)
1
0
000
f
(s)×f
(s)−
f 0 (s)×f 00 (s)
kf 00 (s)k
kf 00 (s)k3
La torsión esta dada por
B 0 (s) = τ (s)N (s) ⇒ B 0 (s)·N (s) = τ (s)N (s)·N (s) ⇒ B 0 (s)·N (s) = τ (s)kN (s)k2 ⇒ B 0 (s)·N (s) = |τ (s)|
Vamos a calcular B 0 (s) · N (s) tenemos que
00
f (s) · f 000 (s)
f 00 (s)
1
0
000
0
00
f
(s)
×
f
(s)
−
=
f
(s)
×
f
(s)
·
kf 00 (s)k
kf 00 (s)k3
kf 00 (s)k
(
00
(((00(
f (s) · f 000 (s) (
1
1
0
000
00
0 (((
00
(f (s) × f (s) · f (s) = 00
f (s) × f (s) · f (s) −
f 0 (s) × f 000 (s) · f 00 (s)
(
(
00
2
00
4
2
(
(
kf (s)k
kf
(s)k
kf
(s)k
(
(
(
La cancelación es porque
f 0 (s) × f 00 (s) · f 00 (s) = 0
y como
k(s) = kf 00 k
se tiene entonces que
τ (s) =
f 0 (s) × f 000 (s) · f 00 (s)
f 0 (s) × f 00 (s) · f 000 (s)
=
−
k(s)2
k(s)2
Facultad de Ciencias UNAM
Prof. Esteban Rubén Hurtado Cruz
Cálculo Diferencial e Integral III
Introducción a las Funciones Vectoriales (Funciones de R → Rn )
3
Ahora vamos a expresar la torsión en términos de t, se tiene que Ya hemos visto que
T (s) = f 0 (s) =
f 0 (t)
kf 0 (t)k
Por lo tanto
T 0 (s) = f 00 (s) =
d
f 0 (t)
kf 0 (t)k
dt
d
f 0 (t)
kf 0 (t)k
ds
d
=
f 0 (t)
kf 0 (t)k
dt
d
dt
=
ds
f 0 (t)
kf 0 (t)k
1
ds
dt
dt
d
=
f 0 (t)
kf 0 (t)k
dt
ϕ0 (s) =




d(kf 0 (t)k)
f 0 ·f 00
kf 0 (t)kf 00 − f 0 (t) kf
0 (t)k
kf 0 (t)kf 00 − f 0 (t)
1
1
1
dt


=
= 
0
0
2
0
0
2
0
|{z}
kf (t)k
kf (t)k
kf (t)k
kf (t)k
kf (t)k
∗
Donde *
p
d f 0 (t) · f 0 (t)
d (kf 0 (t)k)
f 0 (t) · f 00 (t)
=
=
dt
dt
kf 0 (t)k
Por tanto


0
f 0 ·f 00
kf 0 (t)kf 00 − f 0 (t) kf
0 (t)k
kf (t)k2 f 00 − (f 0 · f 00 ) f 0
1
1
1


=
= 0 4 kf 0 (t)k2 f 00 − (f 0 · f 00 ) f 0
0
2
0
0
0
3
kf (t)k
kf (t)k
kf (t)k
kf (t)k
kf k
Por lo tanto
1
kf 0 (t)k2 f 00 (t) − (f 0 (t) · f 00 (t)) f 0 (t)
0
4
kf k
f 0 (t)
1
0
00
0
2 00
0
00
0
f (s) × f (s) = 0
×
kf (t)k f (t) − (f (t) · f (t)) f (t) =
kf (t)k
kf 0 k4
0
1
1
f (t) · f 00 (t)
0
0
0
00
f
(t)
×
f
(t)
=
f
(t)
×
f
(t)
−
f 0 (t) × f 00 (t)
kf 0 (t)k3
kf 0 (t)k
kf 0 (t)k3
f 00 (s) =
(1)
Mientras que
df 00 (s)
f (s) =
=
ds
000
df 00 (s)
dt
dt
=
ds
df 00 (s)
dt
1
ds
dt
=
df 00 (s)
dt
1
kf 0 (t)k
=
1
0
2 00
0
00
0
kf
(t)k
f
(t)
−
(f
(t)
·
f
(t))
f
(t)
=
kf 0 k4
"
0
0
0
#
00
00
1
1
f
(t)
·
f
1
f
(t)
·
f
f 000 (t) +
f 00 (t) −
f 00 (t) − f 0 (t)
kf 0 (t)k
kf 0 (t)k2
kf 0 (t)k
kf 0 (t)k4
kf 0 (t)k4
1
d
0
kf (t)k dt
Por lo tanto hacemos
f 0 (s) × f 00 (s) · f 000 (s) =
0
0
0
00
00
1
1
f (t) · f
1
1 00
f
(t)
· f
f
0
00
000
00
0
f
(t)×f
(t)·
f
(t)
+
f
(t)
−
(t)
−
f
(t)
0 (t)k
0 (t)k4
kf
kf 0 (t)k3
kf 0 (t)k
kf 0 (t)k2
kf
kf 0 (t)k4
Facultad de Ciencias UNAM
Prof. Esteban Rubén Hurtado Cruz
Cálculo Diferencial e Integral III
Introducción a las Funciones Vectoriales (Funciones de R → Rn )
=
1
kf 0 (t)k3
f 0 (t) × f 00 (t) ·
1
kf 0 (t)k3
f 000 (t) =
4
1
kf 0 (t)k6
f 0 (t) × f 00 (t) · f 000
de la igualdad
f 0 (s) × f 000 (s) · f 00 (s)
f 0 (s) × f 00 (s) · f 000 (s)
1
f 0 (t) × f 00 (t) · f 000
=
−
=
−
0 00 2
k(s)2
k(s)2
kf 0 (t)k6
kf ×f k
kf 0 (t)k3
Tenemos que la torsión esta dada por
τ (t) = −
Facultad de Ciencias UNAM
f 0 (t) × f 00 (t) · f 000
(kf 0 (t) × f 00 (t)k)
2
Prof. Esteban Rubén Hurtado Cruz
Cálculo Diferencial e Integral III