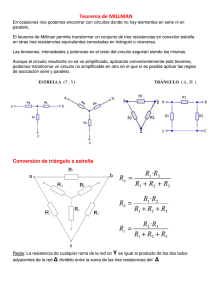
PUENTE DE HILO OBJETIVOS Determinar el valor de una resistencia desconocida. MATERIAL

PUENTE DE HILO
OBJETIVOS
Determinar el valor de una resistencia desconocida.
MATERIAL
Un puente de hilo, un miliamperÃ−metro, un voltÃ−metro, caja de resistencias R, una fuente de
alimentación de c.c. y resistencias desconocidas.
DESARROLLO DE LA PRACTICA
Montamos el circuito de la figura y tomamos los valores de l y lx para seis valores de R y hacer una gráfica
que represente en el eje de ordenadas l / lx y e abscisas l / R.
R ( KS )
1
2.2
3.3
4.7
5.6
10
lx (mm)
230
4.4
501
592
630
755
y
4.35
2.47
1.99
1.68
1.58
1.32
x ( KS )-1
1
0.45
0.303
0.21
0.18
0.1
Rx ( KS )
3.35
3.24
3.28
3.24
3.24
3.24
2. Montamos los siguientes circuitos. Utilizando tres valores de R obtener V1,A1 , V2 , A2 . Construir una
tabla con las lecturas obtenidas y su correspondiente error.
Circuito con resistencias en serie:
R (K S) " 0.05
5.6
3.3
2.2
A (mA) " 0.01
0.59
0.79
0.95
V (v) " 0.01
5.20
5.20
5.20
Circuito con resistencias en paralelo:
R (K S) " 0.05
5.6
3.3
2.2
A (mA) " 0.01
2.53
3.17
3.93
V (v) " 0.01
5.19
5.19
5.19
Hoja de resultados:
Obtener por el método de los mÃ−nimos cuadrados el valor de Rx y su error correspondiente, con los datos
del apartado 1
Xi ( A )
Xi2 ( C )
Yi ( B )
Yi2 ( D )
XiYi(D)
Yi-n (yi´)
XiYi(D´)
1
1
0.450
0.303
0.210
0.180
0.100
3 2.243
1
0.202
0.092
0.044
0.032
0.010
1.381
4.350
2.470
1.940
1.680
1.580
1.320
13.420
18.920
6.100
3.460
2.850
2.560
1.740
36.140
4.350
1.120
0.603
0.357
0.280
0.130
6.847
3.350
1.470
0.940
0.680
0.580
0.320
7.420
3.350
0.660
0.300
0.143
0.104
0.032
4.589
N = 6 m = 3.35 Rx = m = 3.35 " 27.82 %
n = ( CB - AD )/ CN -A2
n = 0.975 " 0.0088
A fin de evaluar la bondad del ajuste obtenido se determina el coeficiente de correlación r.
r = m q(CN - A2 )/ ( FN - B2 ) = 0.997 , por su proximidad a la unidad pensaremos que su ajuste es correcto
2.- Obtener el valor de Rx y su error, como valor medio de los tres valores obtenidos al tomar tres valores
distintos para R en el apartado 2.
Circuito con resistencias en serie:
R + Rx = V / A Y Rx = ( V / A ) - R
Rx = 3.21 K S ; Rx = 3.25 K S ; Rx = 3.27 K S
V = 3 Vi/n = 3.24 K S ; Ea = 0.02 6 Er = 0.6%
R (K S) " 0.05
A (mA) " 0.01
5.6
0.59
3.3
0.79
2.2
0.95
Circuito con resistencias en paralelo:
V (v) " 0.01
5.20
5.20
5.20
Rx (K S) " 0.6%
3.21
3.25
3.27
V (v) " 0.01
5.19
5.19
5.19
Rx (K S) " 0.6%
3.23
3.25
3.30
R@Rx / ( R + Rx ) = V / A Y Rx = VR / ( AR - V )
Rx = 3.23 ; Rx = 3.25 ; Rx = 3.30
V = 3 Vi/n = 3.26 K S ; Ea = 0.02 6 Er = 0.6%
R (K S) " 0.05
5.6
3.3
2.2
A (mA) " 0.01
2.53
3.17
3.93
3.- Comparar los valores de Rx obtenidos por ambos procedimientos. ¿ Que medida serÃ−a mejor?
2
La mejor medida será aquella cuyo error sea menor, su error relativo, en este caso el procedimiento más
correcto serÃ−a el segundo, porque nos muestra un error de tan solo el 0.6%, frente al 27.82% del error del
primer procedimiento.
3