SOLUTION TO AMM PROBLEM # 11384 Problem# 11384 Proposed
Anuncio

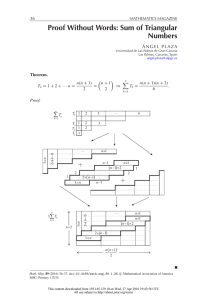
SOLUTION TO AMM PROBLEM # 11384 ÁNGEL PLAZA Problem# 11384 Proposed by Moubinool Omarjee, Lycée Jean-Lurcat, Paris, France. Show that √ ∞ X (−1)⌊ n⌋ (pn n=1 converges. Solution. It is enough to apply the Leibnitz’s Theorem for alternating series. Note that ∞ X (−1)⌊ n=1 pn √ n⌋ = ∞ X n (−1) n=1 2n + 1 < an = p(n+1)2 −1 an − an+1 > X (n+1)2 −1 k=n2 X (n+1)2 −1 k=n2 X 1 = (−1)n an pk n=1 ∞ 1 2n + 1 n→∞ < −→ 0 pk pn2 2n + 3 2n + 1 − >0 p(n+1)2 −1 p(n+1)2 ¤ D EPARTMENT OF M ATHEMATICS , U NIVERSIDAD DE L AS PALMAS DE G RAN C ANARIA , 35017–L AS PALMAS G.C. SPAIN E-mail address: aplaza@dmat.ulpgc.es