EXAMEN DE ESTADÍSTICA DESCRIPTIVA
Anuncio
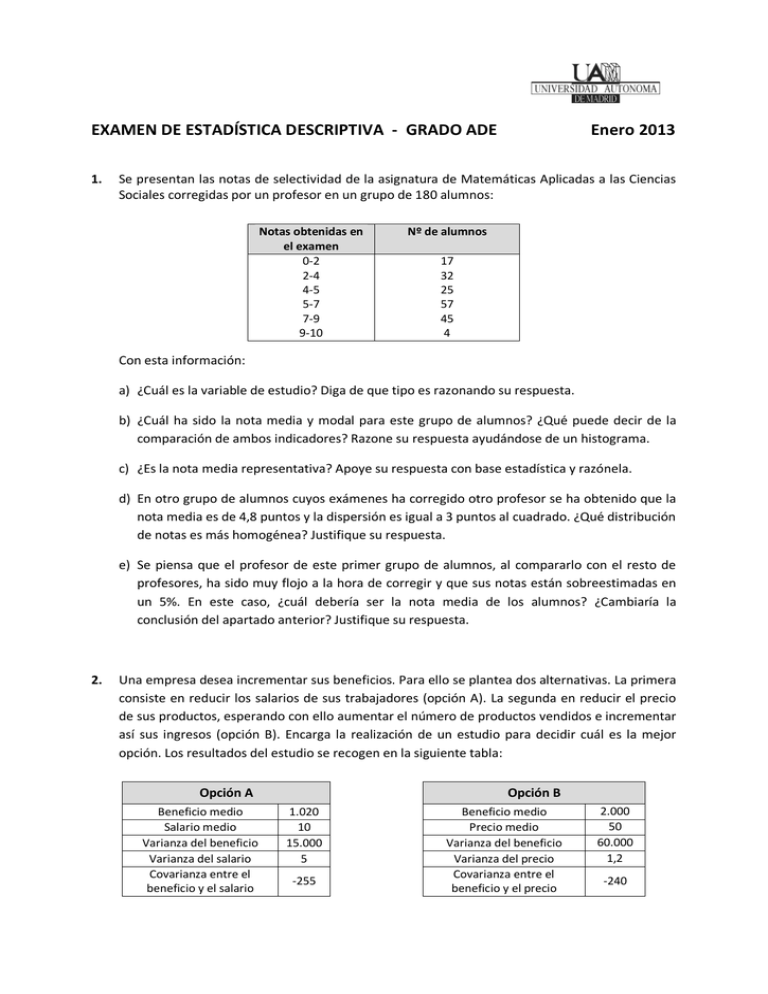
EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE 1. Enero 2013 Se presentan las notas de selectividad de la asignatura de Matemáticas Aplicadas a las Ciencias Sociales corregidas por un profesor en un grupo de 180 alumnos: Notas obtenidas en el examen 0-2 2-4 4-5 5-7 7-9 9-10 Nº de alumnos 17 32 25 57 45 4 Con esta información: a) ¿Cuál es la variable de estudio? Diga de que tipo es razonando su respuesta. b) ¿Cuál ha sido la nota media y modal para este grupo de alumnos? ¿Qué puede decir de la comparación de ambos indicadores? Razone su respuesta ayudándose de un histograma. c) ¿Es la nota media representativa? Apoye su respuesta con base estadística y razónela. d) En otro grupo de alumnos cuyos exámenes ha corregido otro profesor se ha obtenido que la nota media es de 4,8 puntos y la dispersión es igual a 3 puntos al cuadrado. ¿Qué distribución de notas es más homogénea? Justifique su respuesta. e) Se piensa que el profesor de este primer grupo de alumnos, al compararlo con el resto de profesores, ha sido muy flojo a la hora de corregir y que sus notas están sobreestimadas en un 5%. En este caso, ¿cuál debería ser la nota media de los alumnos? ¿Cambiaría la conclusión del apartado anterior? Justifique su respuesta. 2. Una empresa desea incrementar sus beneficios. Para ello se plantea dos alternativas. La primera consiste en reducir los salarios de sus trabajadores (opción A). La segunda en reducir el precio de sus productos, esperando con ello aumentar el número de productos vendidos e incrementar así sus ingresos (opción B). Encarga la realización de un estudio para decidir cuál es la mejor opción. Los resultados del estudio se recogen en la siguiente tabla: Opción A Beneficio medio Salario medio Varianza del beneficio Varianza del salario Covarianza entre el beneficio y el salario Opción B 1.020 10 15.000 5 -255 Beneficio medio Precio medio Varianza del beneficio Varianza del precio Covarianza entre el beneficio y el precio 2.000 50 60.000 1,2 -240 a) Analice mediante una regresión lineal el efecto que, según los resultados obtenidos, va a tener la opción A. b) Analice mediante una regresión lineal el efecto que, según los resultados obtenidos, va a tener la opción B. c) Calcule el coeficiente de determinación (bondad de ajuste) en ambos casos, interprételo y compárelo. d) Según los resultados obtenidos en los apartados anteriores, ¿qué debería hacer la empresa para conseguir su objetivo? Justifique claramente la respuesta. 3. Para realizar un estudio sobre los salarios en la Comunidad Autónoma de Castilla-León se dispone de los siguientes datos referidos a los años 2005-2011: Año Salario medio IPC IPC (miles de €) Base 2002=100% Base 2007=100% 2005 0,9 103% 2006 1,1 110% 2007 1,3 120% 2008 1,47 130% 2009 1,5 138% 2010 1,73 150% 2011 1,85 180% 100% a) Construya la serie de números índice del salario medio con base 100% en el año 2005. b) Calcule los salarios medios en términos reales, a precios constantes de 2007. Comente qué ha ocurrido con el poder adquisitivo de esta Comunidad Autónoma en el periodo de análisis. c) ¿Cuál ha sido el año de mayor y de menor crecimiento salarial en términos reales? d) Calcular la tasa de variación media anual del período 2005-2011 de los salarios en términos nominales y reales. 4. El centro deportivo Francisco Fernández Ochoa decide analizar la evolución que se ha producido en los últimos años de la venta de bonos trimestrales de actividades dirigidas (fitness, pilates, cyclo…): Trimestre 1 2 3 4 2010 76 50 25 33 2011 2012 83 66 28 38 85 68 36 56 a) El investigador ha decidido que la serie de ventas se ajusta a un modelo de agregación multiplicativo ¿qué características presentará entonces la serie? b) Calcule la serie de ventas trimestrales desestacionalizada. c) Interprete el patrón estacional de las ventas trimestrales de bonos. EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE 1. Junio 2013 Según la información ofrecida por el Banco de España, el balance consolidado de las entidades de depósito muestra el siguiente reparto del pasivo en seis tipos de productos financieros (datos en cientos de miles de euros): 2010 2011 Depósitos de las Administraciones Públicas 1,0 0,9 Depósitos de bancos centrales 1,0 2,1 Depósitos de entidades de crédito 5,0 4,7 Valores negociables 5,5 5,3 Otros 5,1 6,1 Depósitos del sector privado 18,1 17,7 TOTAL PASIVO 35,7 36,8 a) En el año 2010 el valor del índice de Gini fue de 0,6. Calcule el índice de Gini para el año 2011 e interprételo. Compare ambos datos. b) Calcule el importe medio del pasivo que tienen las entidades en los distintos productos financieros para el año 2011, ¿considera el dato representativo? Y si se compara con el del año 2010, ¿ha aumentado o ha disminuido su representatividad? c) ¿A cuánto ascendería el pasivo total dentro de 10 años si se mantiene una tasa de variación anual constante igual a la que se ha producido entre 2010 y 2011? 2. Se desea saber el grado de relación entre los años de escolaridad de la madre (X) y la calificación de sus hijos en una prueba de Matemáticas (Y). Los datos recogidos sobre 5 estudiantes se presentan en la siguiente tabla: Estudiante 1 2 3 4 5 Años escolaridad de la madre 8 5 3 6 7 Calificación en Matemáticas 12 8 7 10 10 a) Estime el modelo de regresión lineal simple correspondiente e interprete los resultados obtenidos. b) ¿Se ajusta este modelo a los datos? Justifíquelo estadísticamente. c) ¿Qué parte de la varianza de la variable dependiente viene explicada por la regresión y qué parte es debida a causas ajenas? d) ¿Qué nota obtendría un alumno con una madre escolarizada durante 4 años? 3. Analice la variación del precio del gel de baño durante los últimos 3 años calculando la serie de Índices de Precios de Fisher tomando como base el año 2010. Para ello se dispone de los precios (€) y las cantidades consumidas (miles de unidades) de tres marcas de de gel: NB Palmolive, La Toja y Sanex. Interprete los números índices calculados. NB Palmolive 4. La Toja Sanex AÑOS P Q P Q P Q 2010 2011 2012 1,8 1,85 1,9 40 25 35 1,72 1,75 1,78 45 40 30 1,87 1,95 2,05 25 30 37 Conociendo que la serie trimestral del consumo de medicamentos sigue un modelo de agregación multiplicativo, se dispone de los siguientes Índices de Variación Estacional (IVEs): IVE1 =125%; IVE2 = 78% e IVE4 = 105% El modelo ajustado mediante regresión lineal para captar el componente tendencial es: Tt = 3,11+0,2 · t , siendo t = 1,2,3,… IVEs y modelo tendencial son calculados con la serie de datos de consumo de los años 2008 a 2012, ambos inclusive. Los datos de gasto trimestral del último año: 2012.1 2012.2 2012.3 2012.4 Gasto en medicamento 2 3,5 4 3,8 a) Complete el modelo de estacionalidad e interprete los IVEs correspondientes. b) Obtenga para el año 2012 los datos trimestrales del consumo de medicamentos desestacionalizados. c) Obtenga para el año 2013 una previsión para los gastos médicos trimestrales. Explique cada uno de los pasos realizados. d) Comente el siguiente gráfico del componente irregular o residual obtenido tras el análisis de una serie temporal. EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE Enero 2012 1. En un país de la Unión Europea existen seis cadenas de televisión a nivel nacional. Estas seis cadenas se reparten el mercado de la siguiente manera: Cadena Tele 4 Tele 6 Tele 5 Tele 3 Tele 1 Tele 2 X1: Espectadores país A (millones) 3,2 4,0 5,5 8,6 10,2 12,4 La cadena Tele 3 también opera en otro país de la Unión Europea con el nombre de Canal 3. En este otro país el reparto del mercado es el siguiente: Cadena Canal 2 Canal 3 Canal 4 Canal 1 X2: Espectadores país B (millones) 5,2 9,2 10,0 11,1 a) Determine con base estadística en qué país hay un reparto más equitativo del mercado televisivo. b) Tele 3 y Canal 3 pertenecen a una misma empresa audiovisual ¿En cuál de los dos países tiene la cadena Tele 3/Canal 3 una mejor posición relativa? Razone su respuesta. 2. Según un reciente estudio de una prestigiosa revista científica, el salario inicial percibido por un trabajador con titulación superior depende de la calificación media obtenida en la titulación estudiada. Para analizar esta premisa se ha llevado una encuesta entre los titulados de una universidad que han obtenido su primer empleo. Concretamente, se les ha preguntado cuál ha sido su salario en euros (Y) y su calificación media (X), obteniéndose los siguientes momentos potenciales bidimensionales: 𝑎10= 7,5 𝑎01= 1.328,33 𝑎20= 59,17 𝑎02= 1.774.150 𝑎11= 10.096,67 a) Estime la recta de regresión lineal de Y sobre X. Interprete los coeficientes obtenidos. b) Comente estadísticamente la bondad del ajuste obtenido mediante la regresión. c) ¿Cuál sería la recta de regresión si el salario se hubiera expresado en dólares en vez de euros? El tipo de cambio es de 1,5 dólares por euro. 3. Una empresa opera en España y en Bélgica. Sus cifras de ventas en miles de euros, así como los datos del IPC, en cada país, se muestran en la tabla siguiente: Ventas (miles de €) Año 2006 2007 2008 2009 2010 España 120 130 125 150 146 IPC Bélgica 50 58 70 82 80 España 100% 104% 106% 109% 110% Bélgica 93% 94% 96% 99% 100% a) ¿Cuál ha sido la tasa de variación media anual (tvma) nominal a la que han crecido las ventas en cada país? ¿Cuál ha sido la tvma real en cada país? Comente los resultados. b) Calcule los índices de valor de las ventas en el caso español, tomando como base el año 2006. Interprete el dato obtenido en 2008. c) Suponiendo que la cifra de ventas en cada país crece de forma constante a la tvma nominal obtenida en el primer apartado del ejercicio. ¿Cuánto tiempo tardarían las ventas en Bélgica en alcanzar la cifra de ventas en España? Nota: si no ha sabido calcular las tvma nominales en el primer apartado suponga un valor del 6% para la tvma de las ventas en España y de un 12% en Bélgica. 4. Conociendo que la serie trimestral del consumo de electricidad sigue un modelo de agregación multiplicativo, se dispone de los siguientes Índices de Variación Estacional (IVEs): IVE1 = 1,5; IVE2 = 0,8 e IVE4 = 1,1 así como la recta de regresión estimada para el consumo eléctrico (Yt) en función del tiempo con los datos trimestrales de los años 2005 – 2011: Yt = 3,13 + 0,39 t siendo t = 1, 2, 3, … También son facilitados los datos de consumo trimestral del último año: Consumo eléctrico 2011.1 2,00 2011.2 1,50 2011.3 0,75 2011.4 1,95 a) Complete el modelo de estacionalidad e interprete los IVEs correspondientes. b) Obtenga para el año 2011 los datos trimestrales del consumo de electricidad desestacionalizados. Razone su respuesta estadísticamente y explique cada uno de los pasos realizados. c) Determine la predicción del consumo trimestral para el año 2012. EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE Junio 2012 1. Se quiere realizar un estudio descriptivo de cuatro variables estadísticas obtenidas a raíz de una encuesta realizada a un colectivo de directivos de empresa. Concretamente las variables son: • X1: Años trabajados en la empresa actual. • X2: Número de veces que han asistido al teatro durante el último año. • X3: Satisfacción del directivo con su compañía de telefonía móvil, siendo 1=Nada; 2=Muy poco; 3=Poco; 4=Bastante; 5=Mucho. • X4: Idioma hablado por el directivo, siendo 1=Inglés; 2=Francés; 3=Chino; 4=Italiano; 5=Alemán. Las distribuciones de frecuencias respectivas se presentan a continuación: X1 3 6 7 10 20 Nº de directivos 2 4 6 3 1 X2 2 3 4 5 Nº de directivos 3 6 4 3 X3 1 2 3 4 5 Nº de directivos 1 3 6 4 2 X4 1 2 3 4 5 Nº de directivos 7 4 2 1 2 a) Indique en cada caso qué medida/medidas de posición central utilizaría, justificando su respuesta. b) ¿Qué distribución es más homogénea según el coeficiente de variación de Pearson? Justifique su respuesta. c) ¿Qué puede decir sobre la simetría de la distribución de las variables X3 y X4? 2. Dada la relevancia del consumo eléctrico como indicador coyuntural, un Servicio de Estudios está analizando la evolución anual de dicho consumo. Para ello dispone de los siguientes datos del periodo 2005-2011: Consumo eléctrico (millones de euros) Índice de Precios (base 2002=100%) 2005 3,85 103% 2006 3,87 110% 2007 4,02 120% 2008 4,68 130% 2009 4,90 138% 2010 5,40 150% 2011 6,20 180% a) ¿Cuál es la evolución del consumo de electricidad en términos reales, a precios de 2005? b) ¿Cuál ha sido el año de mayor y el de menor crecimiento en términos reales? c) Calcular la tasa media de variación anual del consumo eléctrico en términos reales habida en el período 2005-2011. 3. El mismo Servicio de Estudios quiere realizar una previsión del consumo de electricidad para el año 2012. Contando con los mismos datos que en el ejercicio anterior, decide estimar un modelo de tendencia mediante un ajuste de regresión lineal. a) ¿Es adecuado este modelo de tendencia para la serie temporal de consumo? Justifíquelo gráficamente. b) Estime la regresión lineal que capte el componente tendencial de la serie de consumo. Interprete los coeficientes del modelo de tendencia obtenido. c) ¿Qué parte de la varianza del consumo eléctrico viene explicada por la regresión y cuál es debida a causas ajenas? 4. En el estudio de la serie trimestral del paro en España (en porcentaje) durante el período 20052010 se ha seleccionado un esquema de agregación multiplicativo. Los IVE han sido: IVE1 = 1,13; IVE3 = 0,80; IVE4 = 1,08 La recta de regresión estimada para la tasa de paro (Yt) en función del tiempo (t = 1, 2, …) ha sido: Yt = 3,6 + 0,8 t a) Interprete el modelo de estacionalidad. b) Realice predicciones del paro trimestral para el año 2011. c) Explique cómo diagnosticaría la validez del modelo a partir del análisis de los residuos. EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE 1. Enero 2011 Hace unos días el Ministerio de Fomento publicó la siguiente información sobre los salarios que perciben los controladores aéreos en España: Salario (decenas de miles de €) 0–9 9 – 18 18 – 27 27 – 36 36 – 45 45 – 54 54 – 99 Número de controladores 48 166 590 701 487 226 145 a) Calcule el salario medio y el salario mediano percibido por los controladores aéreos. ¿Qué puede decir sobre la distribución de los salarios al comparar ambas medidas? b) Calcule el coeficiente de variación de Pearson e interprételo. Si el gobierno plantea reducir el salario de los controladores de forma lineal en 15.000 euros, explique cómo afectaría esta medida al coeficiente de variación de Pearson y calcule el nuevo valor del coeficiente. c) Calcule el coeficiente de asimetría de Bowley o el de Pearson, e interprételo. d) ¿Qué porcentaje de los controladores tiene un salario superior al medio millón de euros? Indique claramente los supuestos realizados para llevar a cabo los cálculos. 2. Para un conjunto de personas que están siguiendo una dieta de adelgazamiento, se han recogido datos sobre el peso perdido desde el inicio de la misma (variable Y, en kilogramos) y el tiempo que llevan siguiendo la dieta (variable X, en semanas), los cuales se muestran en la siguiente tabla: X (semanas) \ Y (kg) 2 4 6 8 10 0-6 4 5 4 6 2 6-10 2 2 5 5 5 10-14 0 1 2 3 4 a) ¿Cuántos kilos en promedio pierden las personas que permanecen 6 o más semanas en el tratamiento? b) ¿Diría usted que siguiendo esta dieta se pierde peso? Explique el procedimiento empleado para contestar a esta pregunta e interprete los parámetros calculados. (Nota: la covarianza entre las variables X e Y es igual a 3,032) c) Según los resultados del apartado anterior, ¿cuántos kilos perdería una persona que lleve ese tratamiento durante 7 semanas? ¿Qué grado de fiabilidad tendrá esa predicción? d) Imagínese que la duración del tratamiento se mide en días en vez de semanas. ¿Cómo se verán alterados los anteriores parámetros de la regresión de Y/X con este cambio? 3. Conforme a los precios y las cantidades de dos productos, consumidas en estos tres últimos años: Año 2008 2009 2010 P1 1 1 3 P2 2 3 1 Q1 0 1 2 Q2 2 1 1 a) Calcule los índices de precios de Paasche, de Laspeyres y de Fisher para el periodo 2008 2010, tomando como base el año 2008. b) Calcule los índices de valor para el periodo 2008 – 2010 (base 2008). c) Calcule la serie de índices de precios de Fisher en base 2010. d) Determine las tasas de variación interanual del índice de precios de Fisher, así como la tasa media anual acumulativa del mismo en el periodo 2008 – 2010. 4. En un Instituto de investigación empresarial se ha realizado un análisis de la serie trimestral de los ingresos nominales (en millones de euros) de una multinacional, desde el año 2006 hasta el 2010 ambos inclusive. Conociendo que la serie sigue un modelo de agregación multiplicativo, se dispone de los siguientes Índices de Variación Estacional (IVEs): IVE1 = 0,65; IVE2 = 2,32 e IVE4 = 0,36 El modelo ajustado mediante regresión lineal para captar el componente tendencial es Tt = 0,86 + 0,42 t , siendo t = 1,2,3,… También son facilitados los datos de ingresos del último año: Ingresos Nominales 2010.1 5 2010.2 7,12 2010.3 6 2010.4 2 d) Complete el modelo de estacionalidad e interprete los IVEs correspondientes. e) Obtenga para el año 2010 los datos trimestrales de ingresos desestacionalizados. Razone su respuesta estadísticamente y explique cada uno de los pasos realizados. f) Determine la predicción de los ingresos trimestrales del año 2011. EXAMEN DE ESTADÍSTICA DESCRIPTIVA - GRADO ADE 1. Junio 2011 Una compañía de seguros, especializada en el ramo de automoción, reúne los datos referentes al beneficio obtenido por las pólizas a todo riesgo para automóviles durante 2010, para cada uno de los distintos niveles de precios, obteniéndose la siguiente información: Precio de la póliza (€) Menos de 85 85-100 100-120 120-150 Mas de 150 Beneficio por póliza (€) 13 27 32 45 58 Porcentaje de pólizas 35% 25% 20% 10% 10% Como información adicional, conocemos también que hay 100 pólizas contratadas de importe superior a 150 euros. Desde estos datos, se le pide que responda a las siguientes cuestiones: a) ¿Diría usted que el beneficio medio de una póliza contratada en esta compañía es representativo? Razone su respuesta. b) ¿Cree que una gran parte de los beneficios obtenidos por la compañía se concentran en un número reducido de pólizas? Cuantifique su respuesta. c) ¿Qué porcentaje de pólizas costaron menos de 100 euros? ¿Qué porcentaje de beneficios representaron tales pólizas? d) Ante el gran aumento de los siniestros, la empresa proyecta una subida en el importe de las pólizas, pero duda entre un aumento lineal de 12 euros y uno proporcional del 12%. ¿A partir de qué precio le interesará a un cliente la subida lineal de 12 euros en su póliza? 2. A los estudiantes de un grupo de grado de la universidad se les ha pasado un cuestionario tipo test de diez preguntas y los resultados los hemos contrastado con el número de convocatorias consumidas hasta la fecha. Teniendo en cuenta que cada acierto corresponde a 1 punto (variable Y) y que el número de convocatorias consumidas es de 0 a 6 (variable X), se ha obtenido la siguiente tabla de correlación: X (conv.) \ Y (ptos.) 0-1 1-3 3-6 a) b) c) d) 0-5 10 3 2 5 - 10 13 7 5 ¿Son independientes la puntuación obtenida y el número de convocatorias consumidas? Calcule las rectas de regresión de Y/X y de X/Y. Calcule el coeficiente de correlación lineal e interprete el resultado. Comente el grado de bondad del ajuste realizado. ¿Cuál es el porcentaje de causas ajenas a la regresión de Y/X que influyen en la variable dependiente? ¿Y en la de X/Y? Razone su respuesta. e) ¿Qué parte de la varianza de la puntuación es explicada por el número de convocatorias? ¿Qué parte no? 3. Se quiere analizar la evolución del poder adquisitivo de los ciudadanos de una determinada provincia en los últimos cinco años. Para ello se dispone de los ingresos anuales totales y del Índice de Precios al Consumo (IPC): Ingresos totales 2005 2006 2007 2008 2009 IPC (millones de €) (2000=100%) 15,35 17 18,5 21,12 24 90% 98% 115% IPC (2009=100%) 120% 110% 100% a) ¿Cuál es el valor de los ingresos anuales en términos reales a precios de 2009? Explique todos los pasos que ha seguido e interprete los resultados. b) Calcular las tasas de variación interanuales en términos reales y nominales. Interprete los resultados. c) ¿Cuál ha sido la tasa media anual acumulativa en términos nominales y en términos reales? Interprete los resultados. d) ¿Qué relación existe entre las tasas interanuales y la tasa media anual acumulativa? 4. Se ha dispuesto de la siguiente información correspondiente al precio (en miles de euros) de un instrumento de medida de alta precisión: Cuatrimestre 1 2 3 2008 21,3 20,8 20,8 2009 23,9 23,3 23,2 2010 26,1 26,1 25,7 Una vez realizado el análisis de la serie temporal, se han obtenido los siguientes resultados: Tt = 20 + 0,7t IVE1 = 1,05 IVE3 = 0,95 a) Interprete el modelo de tendencia. b) Complete e interprete el modelo de estacionalidad. c) Calcule la serie del componente residual y realice un diagnóstico de la validez del modelo planteado a través del gráfico de los residuos.