Descargar el archivo PDF - Revistas Universidad Santo Tomás

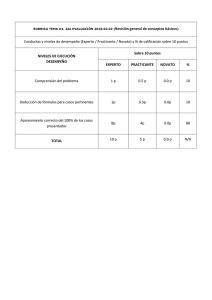
MODELAMIENTO MATEMATICO EN DEPORTES EXTREMOS: SKYDIVING
Jairo A. Coral-Campaña
Departamento de Ciencias Básicas, Universidad Santo Tomas, Bogotá, Colombia.
jairocoral@usantotomas.edu.co
Resúmen
Se desarrolla un modelo matemático para el descenso en paracaídas de un practicante de
skydiving. El modelo propuesto sirve como guía para el planteamiento y desarrollo de un
modelo matemático para algún problema general de ingeniería. El modelo describe con
buena aproximación el descenso del deportista y se podría aplicar en el diseño de un
sistema de control activo que garantice la apertura oportuna del paracaídas, permitiéndole
disfrutar un descenso prolongado sin apertura para la realización de sus acrobacias y
evitando a la vez que se sobrepase el punto de quiebre (breakpoint) para evitar un final
catastrófico.
Palabras Clave: Modelamiento, caída libre, fricción, fluidos, paracaidismo.
Introducción
El skydiving (paracaidismo) es un deporte extremo que consiste en saltar desde un avión o
helicóptero y caer libremente bajo acción de la gravedad reduciendo la velocidad final con
ayuda de un paracaídas. Durante el descenso, el practicante puede ejecutar acrobacias
mientras no se abra el paracaídas, es decir mientras experimenta una caída libre; una vez se
abre el paracaídas podrá experimentar un vuelo en paracaídas o simplemente podrá reducir
su velocidad final para garantizar un aterrizaje sin consecuencias lamentables [1],[2]. El
modelo matemático que se propone en este artículo permite el diseño de un dispositivo de
activación automática (AAD) que abre el paracaídas a una altura determinada si detecta que
el deportista todavía está en caída libre. Esto le permitirá disfrutar de este deporte extremo
al máximo, brindando seguridad adicional, ya que la mayoría de lesiones y muertes que se
producen practicando skydiving suelen suceder porque el paracaidista realiza maniobras
peligrosas o porque cometió un error de juicio que resultó en un impacto a alta velocidad
1
con el suelo. El modelo se basa en la dinámica de un cuerpo (el deportista) que se mueve
en un fluido bajo la acción de la gravedad.
Identificación y Clasificación de Variables
El conjunto de variables que pueden considerarse para el caso más sencillo son:
1. Asociadas al practicante.

Masa (

Posición (

Velocidad (

Area tranversal frontal expuesta al aire (
).
).
).
).
2. Asociadas al paracaídas

Masa (

Area transversal frontal expuesta al aire (

Coeficiente relacionado con la forma del paracaídas abierto ( ).
).
) (paracaídas abierto).
3. Asociadas al Medio

Densidad del aire ( ).

Viscosidad ( ).

Presión atmosférica. ( ).

Temperatura del medio ( ).
De este conjunto de variables, se considera que la variable dependiente es la posición
(altura) del practicante, obviamente sus valores están condicionados a los cambios de
velocidad asociados con la fuerza de gravedad y la fuerza debida a la resistencia del aire.
Estas fuerzas dependen de ciertos valores que se pueden considerar como parámetros del
sistema, tales como la masa, el área de sección transversal, la densidad del aire, la
temperatura, la presión. Para este caso se supone que no hay variaciones de temperatura
durante el lanzamiento del practicante, también se supone que la presión atmosférica se
2
mantiene constante en el rango de altura sobre el nivel del mar que se desarrolla el salto.
También se supone que la aceleración de la gravedad se mantiene constante en este
intervalo. La variable independiente es el tiempo [3],[4],[5].
Planteamiento y Desarrollo del Modelo
El análisis del problema propuesto se puede hacer según el siguiente esquema
metodológico:

En primera aproximación, se deja de lado ciertos aspectos que se consideran
secundarios o despreciables.

Aplicar las leyes de Newton puesto que en este caso se trata de un sistema sometido
a la acción de fuerzas externas. De aquí resultan las ecuaciones de movimiento
respectivas.

Efectuar un análisis matemático y hallar las soluciones de las ecuaciones de
movimiento.

Interpretar físicamente estas soluciones.

Introducir alguna corrección importante a los modelos iniciales y hallar e interpretar
las nuevas soluciones.
Cuando un cuerpo se mueve a través de un fluido (como un gas o un líquido) experimenta
una fuerza de fricción (o arrastre) que aumenta con la velocidad del cuerpo relativa al
fluido. Esto se debe a que, cuando el cuerpo se mueve por el fluido, tiene que empujar las
moléculas de éste y hacerlas a un lado, transfiriéndoles momentum. Entre más rápido se
mueva el cuerpo, más grande será la tasa de transferencia de momentum, es decir, mayor
será la fuerza de fricción o arrastre.
A una velocidad relativamente baja, la fuerza de fricción es aproximadamente proporcional
a la velocidad del cuerpo y opuesta a ella, de tal manera que se puede escribir:
(1)
3
donde ν es el coeficiente de viscosidad del fluido y K es el coeficiente de arrastre. El
coeficiente de viscosidad ν depende de las propiedades moleculares del fluido. El
coeficiente de arrastre K depende de la forma y del tamaño del cuerpo, y se debe obtener
experimentalmente, aunque en algunos casos también se puede calcular.
Cuando el cuerpo se mueve a través de un medio viscoso bajo la acción de una fuerza F, la
fuerza resultante es
y la ecuación de movimiento es:
(2)
Suponiendo que la fuerza F es constante, la aceleración
aumento en
produce un aumento en
y un
. Esto a su vez trae como resultado la disminución de la aceleración. En ese
instante la aceleración también es cero y ya no hay aumento de velocidad: la fuerza
aplicada está balanceada exactamente por la fuerza de fricción del fluido. La partícula
continúa moviéndose en dirección de la fuerza F pero con velocidad constante, denominada
velocidad límite o terminal. Esta velocidad se puede determinar haciendo
en la
ecuación (2), y se obtiene:
(3)
De acuerdo con el principio de Arquímedes, la fuerza de empuje ejercida por el fluido es
igual al peso del fluido desplazado por el cuerpo[6]. En consecuencia, la ecuación (3) se
transforma en:
(4)
4
donde V es el volumen del cuerpo, y
y
la densidad del cuerpo y la del fluido,
respectivamente. Cuando la densidad del cuerpo es mucho mayor que la del fluido, como es
el caso de un cuerpo sólido que cae en el aire, el empuje puede ignorarse.
La expresión
es una descripción fenomenológica de una fuerza estadística. No
expresa una ley fundamental, sino que es una aproximación conveniente cuando la
velocidad del cuerpo relativa al fluido es pequeña. Para velocidades relativas grandes, como
es el caso de este problema, necesitamos usar otra expresión para la fuerza de fricción, que
puede ser proporcional al cuadrado de la velocidad. Por ejemplo, se puede tomar:
(5)
donde
es la densidad del aire, A es la sección transversal frontal expuesta al aire y
es un
coeficiente que depende de la forma del objeto [7].
Ahora bien, la densidad del aire varía con la altura, pero en el modelo propuesto se tomará
como constante a lo largo de la trayectoria del practicante. El área A también varía de
acuerdo a las posiciones que tome el practicante a la hora de realizar sus acrobacias y
obviamente a la hora de abrir el paracaídas. En el modelo se propone que
siendo
constante y representa el área del practicante a pesar de sus acrobacias. Cuando abra el
paracaídas,
donde
paracaídas. El coeficiente
representa el área transversal, expuesta al aire, del
depende de qué tan aerodinámico sea el practicante; por
ejemplo para un disco circular
, para una esfera
, para un avión
[7].
Consideremos el esquema de la figura 1. Tomando la dirección positiva de nuestro sistema
de coordenadas hacia abajo, la aplicación de la Segunda Ley de Newton sobre la masa del
practicante conduce a:
5
(6)
El practicante desciende debido a la acción de la gravedad, aumentando su velocidad hasta
que la fuerza de fricción del aire balancea la fuerza de gravedad. A partir de ese momento
el practicante continúa el descenso con velocidad constante, la velocidad terminal:
(7)
Figura 1: Fuerzas sobre el deportista o practicante de skydiving cayendo.
El valor de la velocidad terminal es independiente de la velocidad inicial como se muestra
en la figura 2.
Figura 2: Variación de la velocidad en función del tiempo para diferentes velocidades
iniciales.
6
Para encontrar la velocidad en cualquier instante de tiempo, reescribimos la ecuación (6) de
la siguiente manera:
(8)
Ahora integramos esta ecuación entre
y
y entre
y , respectivamente,
(9)
Sea
, entonces
. Con este cambio de variable se tiene:
(10)
Empleando una tabla de integrales, y considerando el caso especial en que la velocidad
inicial es
se puede llegar a:
(11)
Podemos entonces integrar nuevamente esta ecuación y considerar que para
máxima y es
la altura es
, de tal manera que encontramos la posición en función del tiempo, esto es:
7
(12)
A partir de la ecuación (6) podemos obtener también una expresión que relacione la
posición con la velocidad. Tomemos entonces:
(13)
reemplazando esta ecuación en la expresión (6) se encuentra:
(14)
Integramos esta ecuación entre
y
y entre
y :
(15)
de donde:
(16)
despejando
en términos de
se llega a que:
8
(17)
Para resolver el problema planteado es necesario estimar una velocidad máxima adecuada
de llegada al suelo para evitar catástrofes. Para esto se supone que es posible que una
persona se lance desde una altura de
m (aproximadamente un piso) y que llegue al suelo
sin sufrir alguna lesión. Entonces, si esa persona se lanza hacia abajo sin velocidad inicial,
el tiempo que tarda en llegar al suelo es:
(18)
Con esta aproximación, la velocidad con la que llega al suelo es:
(19)
Se puede considerar entonces que una velocidad razonable de llegada podría ser
m/s.
Esta velocidad corresponde a la velocidad terminal o final del deportista con el paracaídas
abierto. Entonces podríamos ver cuánto debería ser el área aproximada de sección
transversal frontal del paracaídas, si consideramos que una persona con su equipo pesa
alrededor de
kg/
kg, tomando el valor de la densidad del aire al nivel del mar
y un coeficiente de forma
(tomado como el promedio de los factores de
forma para un disco circular y para una esfera),
(20)
9
despejando
se llega a que:
(21)
De acuerdo con la bibliografía, un diámetro promedio de un paracaídas es de alrededor de
m [8]. Si lo consideramos como un casquete esférico, el área de sección transversal
frontal expuesta al aire sería
.
Consideremos ahora otra situación: el deportista con el paracaídas cerrado. Según la
bibliografía, dependiendo del estilo de salto, de la masa del practicante y de la posición que
se adopte durante la caída, la velocidad terminal oscila alrededor de unos
km/h, es
m/s [9]. Para este caso consideramos que no se hacen muchas acrobacias en
decir unos
el aire y más bien, el área de sección transversal permanece constante. Tomamos el mismo
valor para el coeficiente de forma y encontramos
de la misma manera que en el párrafo
anterior. El cálculo arroja un valor de
. Una persona de estatura promedio
(
unos
m) que se lanza en posición águila podría aportar con unos
m de longitud y con
m de ancho para dar como resultado un área efectiva de aproximadamente
.
Independientemente de la altura desde la cual se lanza el practicante, si consideramos que
parte con una velocidad vertical
m/s, se puede encontrar la distancia que recorre
hasta alcanzar la velocidad terminal. En el peor de los casos, la aceleración será la de la
gravedad y no habrá fuerza debida a la resistencia del aire. Estamos entonces, calculando
un caso extremo. Esto es:
(22)
que con el valor predicho de
m/s se encuentra que
s y durante este tiempo
(bajo las mismas consideraciones extremas) habrá recorrido una distancia de:
10
(23)
Ahora veamos la situación de apertura del paracaídas. Es importante ver cuál sería la
distancia que recorre desde que se abre el paracaídas hasta que alcanza la nueva velocidad
terminal. Partamos entonces de que el practicante está descendiendo con una velocidad
constante de
que
m/s y que su área de sección transversal es
kg/m. La nueva velocidad final es
, de tal manera
m/s. La
desaceleración producida por la apertura del paracaídas es:
(24)
Con esta desaceleración encontramos la distancia deseada a partir de (en una
aproximación):
(25)
Hasta el momento se ha encontrado que aproximadamente
m se
emplean en acrobacias necesarias de aceleración y desaceleración. Unos
m son
necesarios para poder desacelerar hasta alcanzar la velocidad adecuada de llegada. Esta
distancia está relacionada con la masa de la persona. Existen unos tipos de saltos en los que
el practicante va acompañado de un guía, esto duplicaría la masa, reduciría a la mitad la
desaceleración y la distancia requerida podría aumentar hasta unos
m. En medio de las
aproximaciones consideradas se podría tomar un límite máximo (mínimo) de distancia con
respecto al suelo de
m para evitar desastres. Este valor va de acuerdo con las
suposiciones y valores tomados en líneas anteriores y cambios fuertes en alguno de esos
parámetros podrían indicar que la distancia sea mayor.
11
Los saltos más comunes (más económicos) que se sugieren para principiantes se realizan
desde una altura de
m. Podemos ver qué tan larga puede ser la aventura de uno de
estos practicantes: De esos
aproximadamente
m restamos
m en los que se acelera desde la partida hasta alcanzar la velocidad
terminal con paracaídas cerrado. Quedan entonces
velocidad terminal es de
aproximadamente
m necesarios para el aterrizaje y
m de pura adrenalina. Si la
m/s, significa que el practicante dispondrá de
s para realizar todas sus acrobacias, o simplemente disfrutar.
Resultados del Modelo
Con estos datos propuestos es posible elaborar gráficas de velocidad vs tiempo (Figura 3) y
velocidad vs posición (Figura 4) para dos tramos distintos: El primer tramo es desde que el
practicante salta hasta que alcanza su velocidad límite; el segundo tramo es desde que se
abre el paracaídas hasta que se alcanza la nueva velocidad límite. Tomaremos entonces una
altura del salto de
m/s,
m,
m/s y
m/s y una altura inicial de
m/s para el primer tramo; y
m para el segundo tramo. (En este caso
tomamos nuestro sistema de coordenadas con el eje positivo hacia arriba, de manera que
las velocidades estarán dirigidas hacia abajo y por eso su signo).
(a) Velocidad primer tramo
(b) Velocidad segundo tramo
Figura 3: Variación de la velocidad en función del tiempo para el primer y segundo
tramo.
12
(a) Velocidad primer tramo
(b) Velocidad segundo tramo
Figura 4: Variación de la velocidad en función de la posición para el primer y
segundo tramo.
En las gráficas de velocidad vs posición aparecen velocidades positivas, pero de antemano
se sabe que están dirigidas hacia abajo y que el suelo equivale al punto
m.
En las gráficas de la Figura 3 podemos apreciar que se requieren aproximadamente 20 s
para alcanzar la velocidad límite desde que se inicia el salto. Luego de este tiempo el
deportista cuenta con algunos segundos más disfrutando a velocidad constante y luego se
abre el paracaídas. Una vez se abre el paracaídas se requiere cerca de 1 s para alcanzar la
velocidad final. En las gráficas de la Figura 4 se aprecia que la velocidad límite se alcanza
pasados los primeros 1000 m de recorrido y luego se requieren menos de 20 m para pasar
de esa velocidad límite a la velocidad final.
Finalmente, podemos elaborar gráficas de posición en función del tiempo (Figura 5) para
los dos tramos considerados. En el primer tramo, como se muestra en la Figura 5, el
practicante desciende alrededor de 1000 m en un movimiento acelerado hasta alcanzar la
velocidad límite, en aproximadamente 20 s desde su lanzamiento.
Conclusiones
El modelo propuesto es bastante sencillo, con algunas suposiciones, pero describe, en muy
buena aproximación, el salto en paracaídas y se puede utilizar como herramienta de apoyo
en el diseño de algún sensor que permita seleccionar el momento adecuado para el
13
despliegue del paracaídas, o para iniciar maniobras de emergencia como último recurso.
Esto se podría hacer con sensores de velocidad y altitud, y con los valores predichos por el
modelo se aseguraría el despliegue automático del paracaídas.
El artículo, en general, también sirve como una guía para el planteamiento y desarrollo de
un modelo matemático para algún problema particular de ingeniería.
Es conveniente aclarar que en este artículo no se muestra la única forma de solucionar el
problema propuesto, simplemente es una opción que con las suposiciones correctas es
capaz de aproximarse en buena medida a la situación física real.
Se invita a los lectores a que hagan las mejoras que crean convenientes al modelo
presentado o tal vez que sugieran otras suposiciones que permitan acercarse aún más a la
situación real.
(a) Posición primer tramo
(b) Posición segundo tramo
Figura 5: Variación de la posición en función del tiempo para el primer y segundo
tramo.
Bibliografía
[1] Extraído el 23 de junio de 2012 de
http://en.wikipedia.org/wiki/Parachuting
14
[2] Extraído el 23 de junio de 2012 de
http://www.1olav.com/en/freefly/what-is-freefly/
[3] Giorgetti, Marcius (1999). Formulation and Development of Mathematical Models for
Engineering Problems: An experience on the Integration of Theory and the Laboratory.
University of Sao Paulo, Brazil.
[4] Giorgetti, Marcius (1999). Formulation and Development of Mathematical Models for
Engineering Problems: An Active-Inductive Approach. University of Sao Paulo, Brazil.
[5] Giorgetti, Marcius(2001). Mathematical Simulation of Engineering Problems: On the
Art of Formulation of Mathematical Models. University of Sao Paulo, Brazil. 2001.
[6] Serway, Raymond (1997). Física Tomo I , Cuarta Edición. Ed. McGraw Hill.
[7] Extraído el 30 de junio de 2012 de
http://www.sc.ehu.es/sbweb/fisica/dinamica/paracaidista/paracaidista.html
[8] Extraído el 30 de junio de 2012 de
http://en.wikipedia.org/wiki/Parachute
[9] Extraído el 30 de junio de 2012 de
http://hypertextbook.com/facts/JianHuang.shtml (Speed of a Skydiver (Terminal Velocity)
The Physics Factbook™ Edited by Glenn Elert -- Written by his students An educational,
Fair Use website)
15