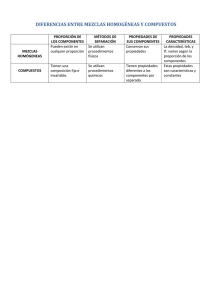
EC.de primer orden y 5 = e 5 ) f(sx,sy) = f(x,y) z = y x y z = ax +by y
Anuncio

EC.de primer orden
y + a(t)y + b(t)y = f(t)
Â
Variables separables
v=e °
− a(x)dx
: y = v(C + °
f(x)
)
v
u  + (2 + 2by p )u + bu 2 = 0
y = f(x, y) e z = − 1
f(x, y)
Â
f(sx, sy) = f(x, y)
y
z= x
y = g(ax + by)
z = ax + by
Â
Ley de Maltus:
p(t) = p o e (b−c)(t−t o )
a x+b y+c
a 1 x + b1 y + c 1 = 0
a 2 x + b2 y + c 2 = 0
Ley logística:
p(t) =
ap o
bp 0 + (a − bp 0 )e −a(t−t o )
si son paralelas:
a1x + b1y + c1
y  = f(
) = g(a 1 x + b 1 y)
k(a 2 x + b 2 y) + c 2
u = x − xc, v = y − yc
a u + b1v
v = f( 1
), homogénea
a2 v + b 2 v
Â
y  + a(x)y + b(x)y n = 0
u = y 1−n
u + (1 − n)a(x)u = (n − 1)b(x)
Â
W [f 1 ...fn ](x) =
si{f 1 , ...f n }son LI e W = ?
y  + P 1 (x)y  + P 2 (x)y = 0
y = yÂz
De existencia y unicidad:
f(t, y) c C o (D)
¹f (t, y) c C o (D)
¹y
existe una única solución
Lineales y coef ctes:
Raíces del polinomio característico
l : multiplicidad
definida en un cierto intervalo.
La solución que no se puede prolongar se denomina
“solución maximal”
De prolongación
Bernouilli
Wronskiano:
f1 - fn
® ¯ ®
f n−1)
- f n−1)
n
1
y 1 z  + (2y Â1 + P1 y 1 )z  = 0
Teoremas
si
si no, buscar puntos de corte:
Ecuación homogénea
Método d’Alembert: Para reducir el orden
Reducibles a homogéneas
y  = f( a 21x+b 21y+c 21 )
y n) = f(x)
si{f 1 , ...f n }son LD e W = 0
Modelos de población
Â
Del tipo
Reducción de orden
Trayectorias ortogonales
Cambios
Homogéneas
EC.de orden superior
2
y = u + yp
Ricatti
y  + a(x)y = f(x)
Lineal
1
por Jesús Sanz Marcos
Ecuaciones diferenciales
si f(t,y) cumple teorema anterior y su solución maximal tiene un
extremo finito alfa
:|y(t)|
d +º
tda
k : vap
k c ‘ : y j1..l = e k jx $ x 0..l−1
kcŠ:
: y j1 1..l = e Re k j x $ x 0..l−1 $ cos(Im kx)
: y j2 1..l = e Re k j x $ x 0..l−1 $ sin(Im kx)
EC.de primer orden
y + a(t)y + b(t)y = f(t)
Â
Variables separables
v=e °
− a(x)dx
: y = v(C + °
f(x)
)
v
u  + (2 + 2by p )u + bu 2 = 0
y = f(x, y) e z = − 1
f(x, y)
Â
f(sx, sy) = f(x, y)
y
z= x
y = g(ax + by)
z = ax + by
Â
Ley de Maltus:
p(t) = p o e (b−c)(t−t o )
a x+b y+c
a 1 x + b1 y + c 1 = 0
a 2 x + b2 y + c 2 = 0
Ley logística:
p(t) =
ap o
bp 0 + (a − bp 0 )e −a(t−t o )
si son paralelas:
a1x + b1y + c1
y  = f(
) = g(a 1 x + b 1 y)
k(a 2 x + b 2 y) + c 2
u = x − xc, v = y − yc
a u + b1v
v = f( 1
), homogénea
a2 v + b 2 v
Â
y  + a(x)y + b(x)y n = 0
u = y 1−n
u + (1 − n)a(x)u = (n − 1)b(x)
Â
W [f 1 ...fn ](x) =
si{f 1 , ...f n }son LI e W = ?
y  + P 1 (x)y  + P 2 (x)y = 0
y = yÂz
De existencia y unicidad:
f(t, y) c C o (D)
¹f (t, y) c C o (D)
¹y
existe una única solución
Lineales y coef ctes:
Raíces del polinomio característico
l : multiplicidad
definida en un cierto intervalo.
La solución que no se puede prolongar se denomina
“solución maximal”
De prolongación
Bernouilli
Wronskiano:
f1 - fn
® ¯ ®
f n−1)
- f n−1)
n
1
y 1 z  + (2y Â1 + P1 y 1 )z  = 0
Teoremas
si
si no, buscar puntos de corte:
Ecuación homogénea
Método d’Alembert: Para reducir el orden
Reducibles a homogéneas
y  = f( a 21x+b 21y+c 21 )
y n) = f(x)
si{f 1 , ...f n }son LD e W = 0
Modelos de población
Â
Del tipo
Reducción de orden
Trayectorias ortogonales
Cambios
Homogéneas
EC.de orden superior
2
y = u + yp
Ricatti
y  + a(x)y = f(x)
Lineal
1
por Jesús Sanz Marcos
Ecuaciones diferenciales
si f(t,y) cumple teorema anterior y su solución maximal tiene un
extremo finito alfa
:|y(t)|
d +º
tda
k : vap
k c ‘ : y j1..l = e k jx $ x 0..l−1
kcŠ:
: y j1 1..l = e Re k j x $ x 0..l−1 $ cos(Im kx)
: y j2 1..l = e Re k j x $ x 0..l−1 $ sin(Im kx)