P1.- Una cavidad en forma de disco circular de radio 50 mm y

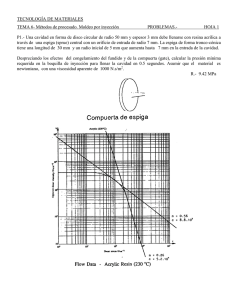
PROBLEMAS PLASTICOS .- LECCION 11 / MOLDEO POR INYECCION
HOJA 1 .
P1.- Una cavidad en forma de disco circular de radio 50 mm y espesor 3 mm debe llenarse con resina acrílica a
través de una espiga (sprue) central con un orificio de entrada de radio 7 mm. La espiga de forma tronco-cónica
tiene una longitud de 30 mm y un radio inicial de 5 mm que aumenta hasta 7 mm en la entrada de la cavidad.
Despreciando los efectos del congelamiento del fundido y de la compuerta (gate), calcular la presión mínima
requerida en la boquilla de inyección para llenar la cavidad en 0.5 segundos. Asumir que el material es
N .s
newtoniano, con una viscosidad aparente de 1000 2 .
m
R.- 9.42 MPa
PROBLEMAS PLASTICOS .- LECCION 11 / MOLDEO POR INYECCION
HOJA 2 .
P2 (SETIEMBRE 2004).- La figura muestra la configuración de un útil de moldeo por inyección, mostrando las
cavidades, para fabricar dos placas idénticas. El camino de flujo, que comienza en la salida del bebedero,
comprende un canal primario, de 8 mm de diámetro y dos canales idénticos secundarios de 5 mmm de
diámetro , cada uno de ellos alimentando a una cavidad. Todos los canales tienen una sección tranversal
circular constante. Las dimensiones de cada cavidad son 150 mm de longitud, 50 mm de ancho y 2 mm de
fondo.
Despreciando los efectos de borde y las pérdidas en la compuerta (gate), calcular la presión mínima requerida
a la salida de la espiga, para llenar las cavidades con resina acrílica en un período de inyección de un segundo.
N.
Si se aplica una presión de 100
a la salida del bebedero, estimar la capacidad de apriete (en kN) requerida
mm 2
de la máquina.
R.- 77 Mpa, 795 kN
PROBLEMAS PLASTICOS .- LECCION 11 / MOLDEO POR INYECCION
HOJA 3.
P3.- Un molde con una cavidad rectangular de 80 mm de largo, 10 mm de ancho y 3 mm de espesor, debe
llenarse con polietileno en un tiempo de 0.5 segundos, a través de un orificio situado en uno de sus extremos.
Despreciando los efectos del congelamiento del fundido, calcular la presión mínima requerida en el orificio de
entrada (gate) para llenar la cavidad. Las propiedades de flujo para el polietileno a 170 ºC se dan en la figura.
Para una presión en el orificio (gate) dos veces la mínima requerida, estimar la fuerza de apriete necesaria
para mantener el molde cerrado durante la inyección.
R.- 11.95 MPa, 14.3 kN
P4 (JUNIO 2004).- La cavidad de un molde para fabricar una placa de Nilón 66, mediante moldeo por
inyección, se alimenta por el centro por medio de un bebedero de forma tronco-conica, como se muestra en la
figura. Despreciando los efectos de flujo radiales, calcular la presión mínima requerida a la entrada de la espiga
para llenar la cavidad en 2 segundos. Asumir que el fundido tiene un comportamiento no newtoniano que sigue
la ley potencial con un índice de consistencia C = 5888 y un exponente n = 0.6.
R.- 25.35 MPa
PROBLEMAS PLASTICOS .- LECCION 11 / MOLDEO POR INYECCION
HOJA 4.
P5. (a).- Los datos de viscosidad, no newtonianos, para el poliestireno de proposito general (GPSS) son los
siguientes:
•
γa
s −1 
102
103
104
105
ηa
 N .s 
 m 2 
596
114
22
4
Mostrar que el comportamiento de dicho material puede ser descrito mediante la ley potencial con n = 0.276
y C = 16711.
(b).- El cuerpo de un bolígrafo se va a fabricar de GPSS por moldeo por inyección. Dicho cuerpo puede ser
modelizado como un tubo hueco circular uniforme, de longitud 125 mm , diámetro medio 7 mm y espesor de
la pared 0.75 mm.
Considerando que la cavidad del molde se alimenta a través de un orificio anular situado en uno de sus
extremos, calcular el tiempo de llenado. para una presión en el orificio de 40 MPa.
R.- 1.48 s
P6.- Calcular la presión mínima requerida en el orificio de entrada a la cavidad rectangular de un molde, de
dimensiones 150mm x 25mm x 3mm, para rellenarla con resina acrílica en un segundo. Se asumirán las
condiciones siguientes:
 N .s 
(a.-) Flujo newtoniano con viscosidad ηa = 1000  2 
m 
(b).- Flujo no newtoniano usando los datos de flujo de la resina acrilica a 230 ºC.
Si la presión en el orifico es 1.5 vesces el valor mínimo calculado, estimar la fuerza de aprietesrequerida para
un molde de impresión doble.
R.- 30 Mpa, 27.3 Mpa, 204 kN
PROBLEMAS PLASTICOS .- LECCION 11 / MOLDEO POR INYECCION
HOJA 5.
P7 (JUNIO 2004).- Se desea fabricar dos piezas moldeadas rectangulares idénticas de Nylón 6 mediante moldeo
por inyección. La disposición del molde es la que se muestra en la figura , y consiste en un canal cilíndrico que
conecta las dos cavidades rectangulares con la salida del bebedero, que esta situada en el centro. Se pide:
(i). – Despreciando los efectos de esquina y las pérdidas en la compuerta, calcular la presión mínima requerida
en la salida del bebedero para llenar las cavidades rectangulares en un período de 0.5 segundos.
(ii) .-Si la presión en la salida del bebedero es dos veces la mínima requerida para llenar el molde, calcular la
fuerza de sujeción o de apriete requerida.
El proceso de inyección se puede asumir que es isotérmico. El polímero fundido es no newtoniano y obedece
un modelo de ley de potencial con las siguientes constantes:
-1
-1
•
Velocidad de deformación por corte  γ  100 s – 1000 s : C = 460, n = 0.82
 
-1
-1
•
Velocidad de deformación por corte  γ  1000 s – 10 000 s : C = 4870, n = 0.47
 
Canal
Longitud = 50 mm
Diámetro = 5 mm
Salida del bebedero
FIGURA
Cavidades 100 mmx40 mmx 2 mm (Espesor)