Tema6.MoldeoInyeccion.ProblemasEnunciados

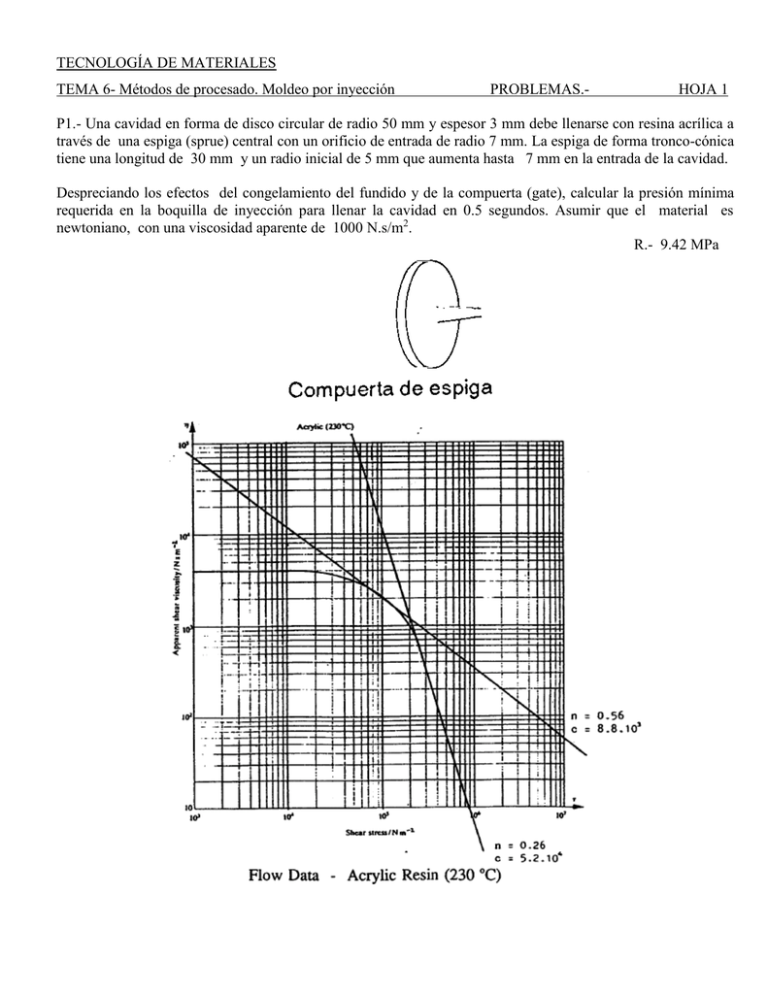
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 1
P1.- Una cavidad en forma de disco circular de radio 50 mm y espesor 3 mm debe llenarse con resina acrílica a
través de una espiga (sprue) central con un orificio de entrada de radio 7 mm. La espiga de forma tronco-cónica
tiene una longitud de 30 mm y un radio inicial de 5 mm que aumenta hasta 7 mm en la entrada de la cavidad.
Despreciando los efectos del congelamiento del fundido y de la compuerta (gate), calcular la presión mínima
requerida en la boquilla de inyección para llenar la cavidad en 0.5 segundos. Asumir que el material es
newtoniano, con una viscosidad aparente de 1000 N.s/m2.
R.- 9.42 MPa
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 2
P2.- La figura muestra la configuración de un útil de moldeo por inyección, mostrando las cavidades, para
fabricar dos placas idénticas. El camino de flujo, que comienza en la salida del bebedero, comprende un canal
primario, de 8 mm de diámetro y dos canales idénticos secundarios de 5 mmm de diámetro , cada uno de ellos
alimentando a una cavidad. Todos los canales tienen una sección tranversal circular constante. Las dimensiones
de cada cavidad son 150 mm de longitud, 50 mm de ancho y 2 mm de fondo.
Despreciando los efectos de borde y las pérdidas en la compuerta (gate), calcular la presión mínima requerida
a la salida de la espiga, para llenar las cavidades con resina acrílica en un período de inyección de un segundo.
Si se aplica una presión de 100 N/mm2 a la salida del bebedero, estimar la capacidad de apriete (en kN)
requerida de la máquina.
R.- 77 Mpa, 795 kN
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 3
P3.- Un molde con una cavidad rectangular de 80 mm de largo, 10 mm de ancho y 3 mm de espesor, debe
llenarse con polietileno en un tiempo de 0.5 segundos, a través de un orificio situado en uno de sus extremos.
Despreciando los efectos del congelamiento del fundido, calcular la presión mínima requerida en el orificio de
entrada (gate) para llenar la cavidad. Las propiedades de flujo para el polietileno a 170 ºC se dan en la figura.
Para una presión en el orificio (gate) dos veces la mínima requerida, estimar la fuerza de apriete necesaria
para mantener el molde cerrado durante la inyección.
R.- 11.95 MPa, 14.3 kN
P4.- La cavidad de un molde para fabricar una placa de Nilón 66, mediante moldeo por inyección, se alimenta
por el centro por medio de un bebedero de forma tronco-conica, como se muestra en la figura. Despreciando
los efectos de flujo radiales, calcular la presión mínima requerida a la entrada de la espiga para llenar la
cavidad en 2 segundos. Asumir que el fundido tiene un comportamiento no newtoniano que sigue la ley
potencial con un índice de consistencia C = 5888 y un exponente n = 0.6.
R.- 25.35 MPa
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 4
P5. (a).- Los datos de viscosidad, no newtonianos, para el poliestireno de proposito general (GPSS) son los
siguientes:

a
s 1 
102
103
104
105
a
 N .s 
 m 2 
596
114
22
4
Mostrar que el comportamiento de dicho material puede ser descrito mediante la ley potencial con n = 0.276
y C = 16711.
(b).- El cuerpo de un bolígrafo se va a fabricar de GPSS por moldeo por inyección. Dicho cuerpo puede ser
modelizado como un tubo hueco circular uniforme, de longitud 125 mm , diámetro medio 7 mm y espesor de
la pared 0.75 mm.
Considerando que la cavidad del molde se alimenta a través de un orificio anular situado en uno de sus
extremos, calcular el tiempo de llenado. para una presión en el orificio de 40 MPa.
R.- 1.48 s
P6.- Calcular la presión mínima requerida en el orificio de entrada a la cavidad rectangular de un molde, de
dimensiones 150mm x 25mm x 3mm, para rellenarla con resina acrílica en un segundo. Se asumirán las
condiciones siguientes:
(a.-) Flujo newtoniano con viscosidad ηa= 1000 N.s/m2
(b).- Flujo no newtoniano usando los datos de flujo de la resina acrilica a 230 ºC.
Si la presión en el orifico es 1.5 vesces el valor mínimo calculado, estimar la fuerza de aprietesrequerida para
un molde de impresión doble.
R.- 30 Mpa, 27.3 Mpa, 204 kN
P7.- Un cierto grado de polietileno en estado fundido obedece a la siguiente ecuación de estado que relaciona la
presión P (en Pa), el volumen específico (m3/ kg) y la temperatura absoluta T:
103 P  3.2x105 103  0.822  2.9x102T
En el estado sólido, a 20 C, la densidad es de 970 kg/m3.
(1).- Determinar la contracción lineal libre de un bloque de polietileno en el enfriamiento uniforme desde 130
°C a 20 °C.
(2).- Si se moldea por inyección, encontrar la presión de empaquetamiento requerida en un producto moldeado,
el cual está sellado con la masa fundida a 130 °C, para asegurar que la contracción lineal en el enfriamiento
hasta 20 °C no exceda del 2 % (Suponer que el enfriamiento es lento).
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 5
P8.- Se desea fabricar dos piezas moldeadas rectangulares idénticas de Nylón 6 mediante moldeo por inyección.
La disposición del molde es la que se muestra en la figura , y consiste en un canal cilíndrico que conecta las dos
cavidades rectangulares con la salida del bebedero, que esta situada en el centro. Se pide:
(i). – Despreciando los efectos de esquina y las pérdidas en la compuerta, calcular la presión mínima requerida
en la salida del bebedero para llenar las cavidades rectangulares en un período de 0.5 segundos.
(ii) .-Si la presión en la salida del bebedero es dos veces la mínima requerida para llenar el molde, calcular la
fuerza de sujeción o de apriete requerida.
El proceso de inyección se puede asumir que es isotérmico. El polímero fundido es no newtoniano y obedece
un modelo de ley de potencial con las siguientes constantes:

-1
-1
Velocidad de deformación por corte    100 s – 1000 s : C = 460, n = 0.82
 
-1
-1

Velocidad de deformación por corte    1000 s – 10 000 s : C = 4870, n = 0.47
 
Canal
Longitud = 50 mm
Diámetro = 5 mm
Salida del bebedero
FIGURA
Cavidades 100 mmx40 mmx 2 mm (Espesor)
P9.- Se ha determinado que una fuerza F es capaz de inyectar un peso dado de un polímero termoestable en el
interior de un molde complejo en 30 s a 177 °C y en 81.5 s a 157 °C. Si la viscosidad del polímero sigue la ley
de Arrhenius, con una velocidad de proceso proporcional a:
e
Q
RT
calcular cuánto tardará el proceso a 227 °C.
R.- 3.5 s
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 6
P10.- Se desean fabricar 8 piezas rectangulares idénticas de polipropileno, cada una de las cuales pesa 10
gramos, mediante moldeo por inyección. Para ello se usa la disposición del molde (Espiga, canales de colada,
compuertas y cavidades) que se muestra en la figura 1. Si el tiempo de inyección es de 2 segundos y la
temperatura del plástico fundido es de 210 ºC, determinar la presión en la entrada de cada cavidad sabiendo que
la presión en la salida de la espiga es de 80 MN/m2.
La densidad del polipropileno es de 909 kg/m3, el volumen de la espiga es de 5000 mm3 y se despreciará el
volumen de las compuertas (gates). El proceso de inyección se puede asumir que es isotérmico y que el fluido
es newtoniano. Se ignorarán las pérdidas de presión en las esquinas.
Las curvas de viscosidad del polipropileno se dan en la figura 2.
Figura 1
Figura 2
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 7
P11.- La mitad de una cinta de cassette tiene la forma dada en la figura 1. Esencialmente es una placa plana de
2 mm de espesor, con tres aberturas. Un cierto fabricante las produce a partir de poliestireno (Difusividad
térmica 1,2x10-7 m2.s). La entrada a la cavidad (gate) se sitúa en la posición A y se usa un molde con 4
cavidades. Para evitar la distorsión del producto durante su eyección del molde se ha determinado que es
necesario esperar hasta que la temperatura media de los productos moldeados (piezas) haya descendido hasta
los 50 ºC. Los productos moldeados iniciales se obtuvieron con los siguientes ajustes de la máquina: Tmolde =
20 ºC, Tfundido = 180 ºC, tciclo = 8 s, lo que conduce a una cantidad de rechazos inaceptable, debido a que
muchas de las piezas presentan grietas en la posición B como se representa en la figura 1. Se piensa que
cualquiera de las alternativas siguientes puede remediar el problema, manteniendo constante el valor de los
otros parámetros:
(i).- Tfundido = 230 ºC y ajuste del tciclo en consecuencia.
(ii).- Tmolde = 40 ºC y ajuste del tciclo en consecuencia.
(iii).- Situación de la entrada a la cavidad en la posición C (esto podría significar el cambio a un molde con dos
cavidades y el nuevo molde costaría 8000 euros).
(1).- ¿Existirán líneas de soldadura en el producto moldeado?.
(2).- Explicar la causa más probable de la aparición de las grietas en la posición B.
(3).- Para cada alternativa (i) a (iii) sugerir porque se puede reducir el riesgo de la aparición de grietas en la
posición B. Calcular el coste de la implementación de cada alternativa, si de desean fabricar un millón de
piezas. Sugerir la mejor solución.
La hora de funcionamiento de la máquina de inyección tiene un coste de 25 euros.
Se supondrá que el valor del número de Biot es grande y se aplicará la ecuación:
  2Fo
TM  Te
8

exp  

Ti  Te  2
4


t
 donde : Fo  2 (Número a dim en s ional de Fourier )
L

donde:
t = Tiempo (s)
L = La mitad del espesor máximo (m).
α = Difusividad térmica (m2.s)
TM = Temperatura media de los productos moldeados para proceder a su eyección (ºC)
Ti = Temperatura del plástico fundido (ºC)
Te = Temperatura de la pared del molde (º C)
Figura 1
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 8
P12.- La disposición de canales de colada de un molde de ocho cavidades se ilustra en la figura. Si el molde
debe ser diseñado de modo que la presión en la entrada de la cavidad (Gate) sea la misma en todos los casos,
determinar el radio del canal de colada en la sección A. Se asume que el flujo es isotérmico.
P13.- El molde mostrado en la figura 1 produce cuatro piezas en forma de copa con el plástico ABS. La
profundidad de las tazas es 60 mm, el diámetro 90 mm y el espesor de pared es de 1,0 mm. La distancia desde
el bebedero a la cavidad es de 40 mm y el diámetro del canal de colada es de 6 mm. Calcular la fuerza de
apriete necesaria en la máquina de moldeo por inyección y estimar como cambiaría la fuerza de apriete si el
molde se diseña con el fin de alimentar las copas a través de una compuerta de aguja en el centro de la base
(como se ilustra en la figura 2). Se utilizarán los datos de fuerza de apriete dados en la figura 3 y se podrá
ignorar la forma cónica de las copas.
Figura 1
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
P13.-
Figura 2
Figura 3
HOJA 9
TECNOLOGÍA DE MATERIALES
TEMA 6- Métodos de procesado. Moldeo por inyección
PROBLEMAS.-
HOJA 10
P14.- En un nuevo diseño para un sistema de estantería de termoplástico, los estantes se reforzarán
longitudinalmente mediante nervios idénticos, con una sección transversal como la que se muestra en la figura.
En el uso la superficie superior será visible. El material que se propone para extruir los estantes es el ABS
(difusividad térmica α= 1,2 X 10-7 m2/s. Para evitar la distorsión, la temperatura media a través del espesor de
cualquier parte del molde no debe ser mayor de 60 °C, después del enfriamiento con agua. Las temperaturas del
polímero fundido y del baño de agua son, respectivamente:
Tfundido = 190 ºC, Tagua = 15 ºC
Para una tasa de producción económicamente viable, el tiempo de enfriamiento no debe exceder de los 10 s.
(1).-Hallar el valor máximo del espesor d en consonancia con el límite de tiempo de enfriamiento.
(2).- Razonar por qué los nervios han de tener sólo el 65 % del espesor de la placa.
(3).- Después de la producción del primer lote de estantes se encuentra que aparecen alabeados (doblados)
después del enfriamiento, con los nervios del lado convexo. Sugerir una razón para ello y proponer un remedio.
P15.- Placas circulares planas, cada una con un agujero circular concéntrico, van a ser producidas mediante
moldeo por inyección usando una compuerta de diafragma central (Figura). Las dimensiones finales a 20 ° C
deben ser: diámetro exterior = 200,0 mm, diámetro interior = 40,0 mm y espesor = 3,00 mm.
El material utilizado será un grado de policarbonato y el molde será de acero con una temperatura del molde de
80° C. Con una configuración particular de los controles de la máquina y cuando la compuerta ha solidificado,
la temperatura media del polímero fundido en la cavidad del molde se ha reducido a 187 ° C y la presión de
compresión es de 30 MPa. Asumiendo un enfriamiento uniforme, estimar la contracción de volumen que se
espera y las dimensiones requeridas de la cavidad del molde a 20 °C (se supondrá que el policarbonato se
comporta isotrópicamente). Determinar los siguientes parámetros del proceso de inyección: fuerza de cierre y
cantidad de material necesaria para cada ciclo expresada en gramos de poliestireno.
Las propiedades del policarbonato amorfo son las siguientes: Tg = 150 °C; coeficientes de expansión térmica
volumétricos: 6.5x10-4 K-1 y 2.1x10-4 K-1 por encima y por debajo de Tg, respectivamente; compresibilidad a
187 ºC: 0.30 GPa-1; densidad del poliestireno: 1060 kg/m3; coeficiente de dilatación térmica lineal del acero:
11x10-6 K-1.