Sistemas Secuenciales
Anuncio

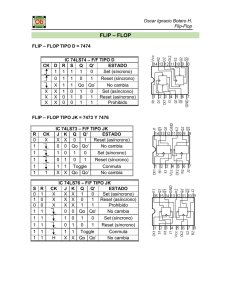
Sistemas Secuenciales Flip-Flops 1 Sistemas Secuenciales Los sistemas digitales se dividen en dos grandes grupos: La Lógica Combinacional implementada através de compuertas lógicas La Lógica secuencial cuya celda básica es el Flip-Flop 2 Sistemas Secuenciales En la lógica combinacional las salidas dependen únicamente de las entradas presentes En la lógica secuencial la salida no solo depende de la entradas presentes, también dependerá de la historia pasada, de lo que sucedió antes. Acá el concepto de tiempo comienza a cobrar sentido. 3 Ejemplos de Sistemas Secuenciales 4 Tipos de circuitos secuenciales Existen dos tipos de circuitos secuenciales – Sincrónicos: Son sistemas cuyo comportamiento puede definirse a partir del conocimiento de sus señales en instantes discretos de tiempo. – Asincrónicos: Depende del orden que cambien las señales de entrada y pueda ser afectadas en un instante dado. 5 Sistemas Sincrónicos Son sistemas que actúan bajo un control de tiempo, este control se denomina reloj (clock). – reloj: es una señal que se alterna entre los valores lógicos 0 y 1 en un periodo regular. 6 Rampas de subida y de bajada reloj 1 Flanco positivo 0 Flanco negativo TPP 7 El Flip-Flop El Flip Flop es un dispositivo de almacenamiento binario con entrada de reloj. Bajo operaciones normales este dispositivo almacenará un 1 ó un 0 y sólo cambiarán estos valores en el momento que ocurra una transición del reloj. 8 Flip-Flop R-S Símbolo Set Normal S entrada Reset Diagrama Q FF R salida Q Salida negada Tabla 9 Ejercicio: Obtenga la tabla de verdad de un FF R-S construido con compuertas NOR 10 Flip Flop R-S Sincronizado Símbolo Set Clock Reset S FF Q Diagrama Normal CLK R Q negada Tabla Modo entrada entrada entrada de Operaci CLK S R on salida salida Q Q efecto Hold 0 0 1 1 No Cambia Reset 0 1 0 1 Reset Q=0 Set 1 0 1 0 Set Q=1 Prohibido 1 1 1 1 no Usar 11 Flip-Flop D Símbolo Lógico Data D Q Diagrama Normal FF Clock CLK Q negada Tabla entrada salida salida salida D Qn+1 Q CLK S FF Q = CLK 0 0 1 1 1 0 R D Q Q FF CLK Q 12 Ejercicio Dibuje las formas de onda Q y Q para el FF D activado con flanco negativo 13 Ejercicios IDEM 14 FF D activado por flanco positivo 15 Flip-Flops con “Clear” y “Preset” Cualquier tipo de Flip-Flop podrá contar con estas entradas asincrónicas, en el caso de Flip-Flops tipo D tenemos: D reloj PRE CLR Q Q PRE CLR D Q Q* 0 1 X X 1 1 0 X X 0 Preset clear 0 0 X X - Inválido 1 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 Normal 16 Ejercicio Dibujar la forma de la salida Q 17 Flip-Flop D Símbolo Preset Data D PS Q Normal FF Clock CLK Q negada CLR Clear Tabla Modo de Operación ENTRADAS Asíncronas SALIDAS Síncronas PS CLR CLK D Q Q Asynchronous Set 0 1 X X 1 0 Asynchronous Reset 1 0 X X 0 1 Prohibited 0 0 X X 1 1 Set 1 1 LaH 1 1 0 Reset 1 1 LaH 0 0 1 18 J-K Flip Flop Símbolo Data Clock Data J FF Q Normal CLK K Q negada Tabla Modo de Operaión ENTRADAS entrada CLK SALIDAS Efecto entrada J entrada K salida Q salida Q Hold 0 0 No Cambia No Cambia No Cambia Reset 0 1 0 1 Reset Q=0 Set 1 0 1 0 Set Q= 1 Toggle 1 1 Toggle Toggle Cambia al Estado opuesto 19 7476 Flip-Flop J-K Símbolo Preset Data Clock Data Normal CLK K CLR Q Complementary Clear Tabla Modo de Operación J FF Q ENTRADAS Asíncronas SALIDAS Síncronas PS CLR CLK J K Q Q Set Asíncrono 0 1 X X X 1 0 Reset Asíncrono 1 0 X X X 0 1 Prohibido 0 0 X X X 1 1 Hold 1 1 0 0 No Cambia No cambia Reset 1 1 0 1 0 1 1 0 Set 1 1 1 0 Toggle 1 1 1 1 Estado opuesto 20 FF J-K 21 Ejercicio Dibujar la salida Q 22 Flip-Flop tipo T (Toggle) Tiene una entrada T, de tal forma que si T = 1, el Flip Flop cambia el valor del estado actual y si T = 0, el estado permanece sin cambios. Tablas de Comportamiento T Q Q* T Q* 0 0 0 0 Q 0 1 1 1 Q 1 0 1 1 1 0 23 Ejercicio Dibujar Q en cada caso: 24 Ejercicio Dibujar las formas de onda de salida en el siguiente sistema secuencial Suponer salidas en alto inicialmente 25 26