TABLA DE INTEGRALES COMUNES EN EL PTV

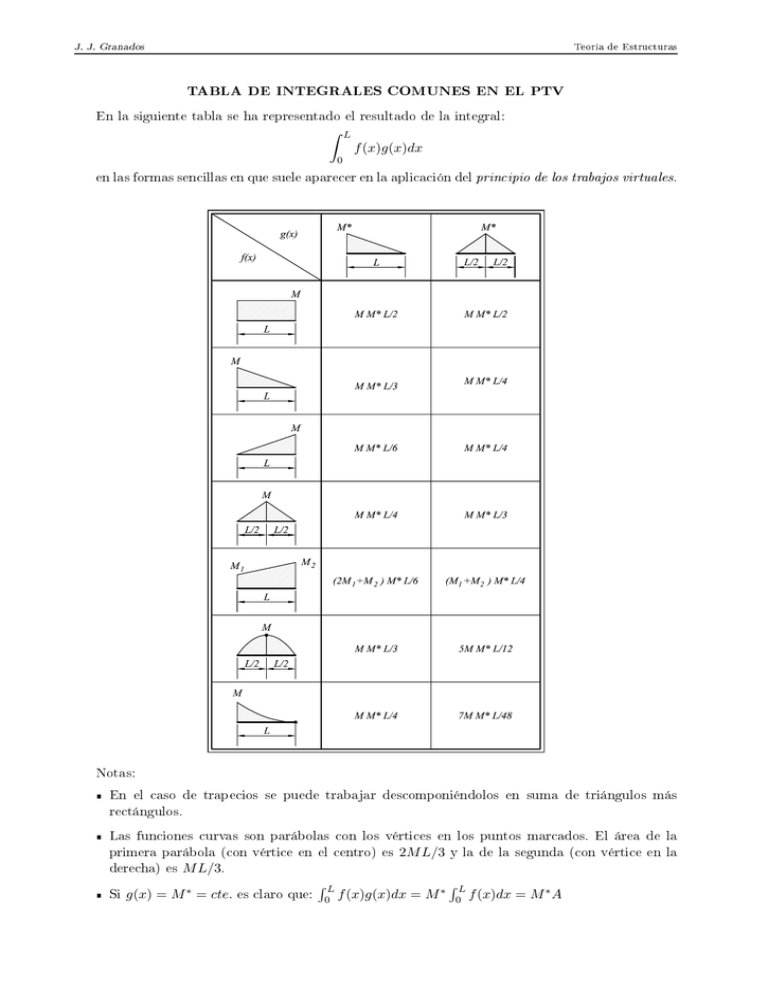
Teoría de Estructuras
J. J. Granados
TABLA DE INTEGRALES COMUNES EN EL PTV
En la siguiente tabla se ha representado el resultado de la integral:
L
Z
f (x)g(x)dx
0
en las formas sencillas en que suele aparecer en la aplicación del principio de los trabajos virtuales.
Notas:
En el caso de trapecios se puede trabajar descomponiéndolos en suma de triángulos más
rectángulos.
Las funciones curvas son parábolas con los vértices en los puntos marcados. El área de la
primera parábola (con vértice en el centro) es 2M L/3 y la de la segunda (con vértice en la
derecha) es M L/3.
Si g(x) = M ∗ = cte. es claro que:
RL
0
f (x)g(x)dx = M ∗
RL
0
f (x)dx = M ∗ A
Teoría de Estructuras
J. J. Granados
MÉTODO DE MULTIPLICACIÓN DE GRÁFICOS
En el caso de tener una función cualquiera f (x), no tiene que ser
continua, y una función lineal g(x) = a + bx, según se indica en la
gura, la integral se puede transformar, quedando:
Z
L
Z
L
Z
0
0
0
L
f (x)xdx =
f (x)dx + b
f (x)g(x)dx = a
= aA + bAxcf = A(a + bxcf ) = Agcf
En el segundo miembro de la primera igualdad, la primera integral
es el área A marcada bajo la curva f (x) y la segunda es el momento
estático de A respecto al origen de x (supuesto en el extremo de la
izquierda). El signicado de gcf = g(xcf ) es el valor de g en el punto
donde está situado el centro de gravedad del área A.
Si la función f (x) tuviese una parte en la que fuese negativa y otra en la que fuese positiva,
existen dos posibilidades:
1. Separar la integral entre la zona positiva y la zona negativa, aplicando el método descrito a
cada una de las zonas.
2. Podemos denir una función auxiliar h(x) que no cambie de signo, para ello bastará sumar
a f (x) una constante. Supongamos que debido a la geometría del problema nos interesa que
h(x) ≥ 0. En tal caso si el mínimo de f (x) fuese −d (con d > 0), la función h(x)sería:
h(x) = f (x) + d, por lo que f (x) = h(x) − d, y utilizando dicha expresión en la integral,
queda:
Z
L
Z
0
L
Z
(h(x) − d)g(x)dx =
f (x)g(x)dx =
0
L
Z
h(x)g(x)dx − d
0
L
g(x)dx
0
Pudiéndose resolver ambas integrales por el método de multiplicación de grácos.