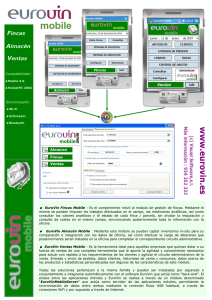
CONFORMACIÓN DEL LÓBULO EN EL ENLACE DE BAJADA CON
Anuncio

UNIVERSIDAD SIMÓN BOLÍVAR Decanato de Estudios Profesionales Coordinación de Ingeniería Electrónica CONFORMACIÓN DEL LÓBULO EN EL ENLACE DE BAJADA CON RETROALIMENTACIÓN REDUCIDA Por Gabriel Castellanos Sartenejas, Noviembre 2007 UNIVERSIDAD SIMÓN BOLÍVAR Decanato de Estudios Profesionales Coordinación de Ingeniería Electrónica CONFORMACIÓN DEL LÓBULO EN EL ENLACE DE BAJADA CON RETROALIMENTACIÓN REDUCIDA Por Gabriel Castellanos Realizado con la Asesoría de Mats Bengtsson PROYECTO DE GRADO Presentado ante la Ilustre Universidad Simón Bolívar como requisito parcial para optar al título de Ingeniero Electrónico Sartenejas, Noviembre 2007 UNIVERSIDAD SIMÓN BOLÍVAR Decanato de Estudios Profesionales Coordinación de Ingeniería Electrónica CONFORMACIÓN DEL LÓBULO EN EL ENLACE DE BAJADA CON RETROALIMENTACIÓN REDUCIDA PROYECTO DE GRADO presentado por Gabriel Castellanos REALIZADO CON LA ASESORIA DE Mats Bengtsson RESUMEN Diferentes esquemas para conformación del lóbulo del enlace de bajada en un sistema celular de múltiples celdas y múltiples usuarios han sido propuestos en la literatura, basados en conocimiento global de los canales existentes entre todas las estaciones base y todas las estaciones móviles. No obstante, en la práctica, una excesiva cantidad de recursos sería requerida para obtener y comunicar la información de los canales. Por otra parte, una determinada estación base sólo debería tener conocimiento preciso de los usuarios que se encuentran fuertemente influenciados por esa base en específico. El propósito de este proyecto consistió en la implementación y evaluación de esquemas capaces de solucionar el problema de conformación del enlace de bajada para cada celda por separado o pequeños grupos de celdas a la vez, mientras son usadas aproximaciones para manejar la interferencia entre celdas distintas. Los algoritmos desarrollados se basaron en métodos de optimización convexa y fueron simulados en un modelo de comunicación celular. Los resultados demostraron que una posible aplicación práctica requiere lidiar con los problemas de control de congestión y la viabilidad de las soluciones. PALABRAS CLAVES (NO MENOS DE TRES) Comunicación celular, downlink beamforming, optimización convexa, arreglos de antenas, SINR, información del estado del canal, algoritmos descentralizados, retroalimentación, filtros espaciales Aprobado con mención: Postulado para el premio: Sartenejas, Noviembre 2007 Reconocimientos Me gustarı́a expresar mi agradecimiento a mi supervisor Mats Bengtsson por haber sugerido el tópico de investigación y por toda la ayuda, consejo y discusiones invaluables. También a la Oficina Internacional del Real Instituto de Tecnologı́a (KTH), especialmente a Cecilia Forsmann, a la Dirección de Relaciones Internacionales y la Coordinación de Ingenierı́a Electrónica en la Universidad Simón Bolı́var por el apoyo recibido y haberme concedido la oportunidad de conducir mi proyecto de grado en Estocolmo. Finalmente, me gustarı́a agradecer a mi familia y amigos por sus palabras de aliento y coraje a lo largo de estos meses de duro trabajo. Índice general 1. Introducción 1.1. Planteamiento del Problema . . 1.2. Metodologı́a . . . . . . . . . . . 1.2.1. Modelo General . . . . . 1.2.2. Algoritmo . . . . . . . . 1.2.3. Ambiente de Simulación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2. Ambiente de Radiocomunicaciones Móviles 2.1. Modelo Celular . . . . . . . . . . . . . . . . . . . . . . . . . 2.1.1. Estaciones Base . . . . . . . . . . . . . . . . . . . . . 2.1.2. Estaciones móviles . . . . . . . . . . . . . . . . . . . 2.1.3. Reutilización de frecuencias . . . . . . . . . . . . . . 2.1.4. Partición de celdas . . . . . . . . . . . . . . . . . . . 2.1.5. Hand-Off . . . . . . . . . . . . . . . . . . . . . . . . 2.2. Ruido e interferencia . . . . . . . . . . . . . . . . . . . . . . 2.2.1. Medios Limitados por Ruido, Medios Limitados por terferencia . . . . . . . . . . . . . . . . . . . . . . . . 2.2.2. Interferencia Celular . . . . . . . . . . . . . . . . . . 2.2.3. Razón de Señal a Interferencia más Ruido . . . . . . . . . . . . . . . . . . . . . . . . . . . In. . . . . . . . . 3. Arreglo de Antenas Transmisoras 3.1. Modelo de Arreglo de Antenna . 3.2. Construcción del lóbulo . . . . . 3.2.1. Uplink Beamforming . . . 3.2.2. Downlink Beamforming . 1 2 3 3 4 4 5 5 5 7 7 8 8 8 9 9 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 11 12 13 13 4. Modelo del canal 4.1. Propagación en Múltiples Trayectorias . . 4.2. Desvanecimiento . . . . . . . . . . . . . . 4.2.1. Desvanecimiento a gran escala . . 4.2.2. Desvanecimiento a pequeña escala 4.3. Modelo de Canal de Banda Estrecha . . . 4.4. Múltiples usuarios y múltiples antenas . . 4.5. Estimación del Canal Downlink . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 15 16 17 17 17 18 19 . . . . . . . . . . . . . . . . 4.6. Retroalimentación . . . . . . . . . . . . . . . . . . . . . . . . . . 20 5. Algoritmos de Conformación del Lóbulo en el Downlink 22 5.1. Conformación óptima del lóbulo . . . . . . . . . . . . . . . . . . . 23 5.1.1. Conformación óptima conjunta del lóbulo y Control de potencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 5.1.2. Algoritmos basados en la dualidad . . . . . . . . . . . . . 24 5.1.3. Programación Semi-Definida y Optimización Convexa . . 25 5.2. Algoritmos Descentralizados . . . . . . . . . . . . . . . . . . . . . 26 5.2.1. Margen SINR Incrementado . . . . . . . . . . . . . . . . . 26 5.2.2. Término de Penalización . . . . . . . . . . . . . . . . . . . 27 5.2.3. Restricciones adicionales . . . . . . . . . . . . . . . . . . . 28 6. Simulaciones y Análisis de Resultados 31 6.1. Ambiente de Simulación . . . . . . . . . . . . . . . . . . . . . . . 31 6.2. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 7. Conclusiones 42 Índice de cuadros 5.1. Solución algorı́tmica de SINR Incrementado . . . . . . . . . . . . 5.2. Solución algorı́tmica por término de penalización . . . . . . . . . 5.3. Solución algorı́tmica con restricciones adicionales . . . . . . . . . 27 28 30 6.1. Parámetros de Simulación . . . . . . . . . . . . . . . . . . . . . . 32 Índice de figuras 3.1. Diagrama de transmisión desde una estación móvil a una estación base en un ambiente urbano . . . . . . . . . . . . . . . . . . . . . 6.1. 6.2. 6.3. 6.4. 6.5. Modelo del ambiente celular simulado: caso de 2 usuarios por celda Convergencia de β para el Algoritmo de SINR Incrementado . . Convergencia de β para el Algoritmo de Término de Penalización Convergencia de β para el Algoritmo de Restricciones Adicionales Convergencia de Iinter /S para el Algoritmo de SINR Incrementado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.6. Convergencia de Iinter /S para el Algoritmo de Término de Penalización . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.7. Convergencia de Iinter /S para el Algoritmo de Restricciones Adicionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.8. Desempeño del Algoritmo de Término de Penalización cuando el parámetro α es variado . . . . . . . . . . . . . . . . . . . . . . . 6.9. Desempeño del Algoritmo de Restricciones Adicionales cuando el parámetro μi es variado . . . . . . . . . . . . . . . . . . . . . . . 6.10. Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de SINR Incrementado, comparado a la Conformación Óptima . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.11. Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de Término de Penalización, comparado a la Conformación Óptima . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.12. Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de Restricciones Adicionales, comparado a la Conformación Óptima . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.13. Potencia Transmitida Total para cada algoritmo de acuerdo al número de usuarios por celda . . . . . . . . . . . . . . . . . . . . 6.14. Probabilidad de Caı́da de Servicio de cada algoritmo de acuerdo al número de usuarios por celda . . . . . . . . . . . . . . . . . . 11 33 35 35 36 36 37 37 38 38 39 39 40 40 41 Glosario Beamforming Conformación del lóbulo CCI Interferencia Co-canal (Co-Channel Interference) CSI Información del Estado del Canal (Channel State Information) Downlink Enlace de bajada FDD División de Frecuencia Duplex (Frequency Division Duplex) QoS Calidad de Servicio (Quality of Service) SINR Razón de Señal a Interferencia más Ruido (Signal to Interference plus Noise Ratio) TDD División de Tiempo Duplex (Time Division Duplex) UCA Arreglo Circular Uniforme (Uniform Circular Array) Uplink Enlace de subida Lista de términos y sı́mbolos θ a(θ) Angulo del móvil Respuesta angular del arreglo σθ Dispersión angular de θ λ Longitud de onda de la señal m Número de elementos de antena ri Señal banda base recibida en el móvil i hi,k ni Vector del canal entre la estación base k y el móvil i Nivel de ruido I(k) Móviles de la celda de k κ(i) Estación base asignada a i wi Vector conformador de i (beamformer) γi Umbral SINR β Constante en el algoritmo de SINR Incrementado α Constante en el algoritmo de Término de Penalización μ Constante en el algoritmo de Restricciones Adicionales Capı́tulo 1 Introducción El excepcional crecimiento de las comunicaciones móviles y las redes inalámbricas obliga a los sistemas de tercera generación (3G) de hoy a adaptarse a un creciente número de subscriptores móviles, accesos de red inalámbricos, servicios móviles y aplicaciones. Se espera que la inminente aparición de los sistemas de comunicación móvil de cuarta generación (4G) solucione problemas aún sin respuesta de los sistemas 3G y provea además una amplia gama de nuevos servicios, como voz y video de alta calidad y canales inalámbricos de datos con alta tasa de transmisión. En estos futuros sistemas inalámbricos, el tráfico será asimétrico: mayor cantidad de información será transmitida desde el punto de acceso hacia el terminal que en la dirección opuesta. Esto implica que el enlace estación basemóvil o enlace de bajada será la porción más crı́tica de la comunicación y donde mayor trabajo habrá que hacer para incrementar la capacidad del sistema. Hoy en dı́a, las proveedoras de servicio de comunicación móvil persiguen la inclusión de más conversaciones telefónicas celulares en el mismo ancho de banda, ası́ como garantizar un mejor servicio a su siempre creciente número de clientes sin necesidad de cambiar por completo la plataforma de red inalámbrica. Esto puede ser logrado al mejorar la detección de data en el enlace estación basemóvil. Existen muchos parámetros que pueden medir este factor, siendo el más importante la Razón de Señal a Interferencia más Ruido o SINR por sus siglas en inglés (Signal to Interference plus Noise Ratio). En cualquier sistema existe una SINR mı́nima que debe ser garantizada para cada usuario con el objeto de mantener la tasa esperada de error de bit debajo de un cierto lı́mite. Ası́, manejar la interferencia se convierte en una parte crı́tica de la optimización del sistema. Un acercamiento práctico y económico para resolver esta situación consiste en usar una estrategia de transmisión y recepción basada en arreglos de antenas (antenna arrays), que poseen la capacidad de cancelar la interferencia de los co-canales (CCI - Co-Channel Interference) [2]. El patrón de radiación del arreglo es ajustado a través de un proceso llamado beamforming o conformación del lóbulo para cumplir los requerimientos deseados. Este proceso consiste en la combinación lineal de señales de diferentes antenas con el peso apropia- 1.1 Planteamiento del Problema 2 do. El lóbulo principal del enlace de bajada o downlink puede ser apuntado electrónicamente desde la estación base en dirección a la estación móvil destino y simultánemente reducir la interferencia en las señales downlink hacia otros móviles. La conformación del lóbulo en el downlink difiere de la conformación del uplink (enlace de subida) porque la escogencia de los vectores peso no sólo afecta el enlace entre el punto de acceso y el usuario destino, sino también a otros móviles tanto dentro como fuera de la celda. Ası́ mismo, si la potencia emitida por la estación base es incrementada de manera innecesaria para forzar la interferencia en su propia celda a cero, la interferencia emitida a las celdas vecinas será incrementada. Por ende, el diseño de conformadores del lóbulo de downlink desde los arreglos de antenas en las estaciones base a los usuarios móviles debe alcanzar un punto de equilibrio donde la potencia transmitida sea minimizada a la vez que se mantienen los requerimientos de calidad de servicio. Diferentes soluciones han sido presentadas (ver el compendio hecho en [8]). Los métodos matemáticos de optimización convexa han sido aplicados en el área de óptima conformación del lóbulo y han arrojado soluciones eficientes con velocidad de convergencia garantizada. Además, resulta muy fácil introducir modificaciones, por ejemplo añadir restricciones extras en el rango dinámico o incrementar la robustez a errores de estimación del canal. De cualquier manera, las soluciones óptimas requieren conocimiento total de los canales en cada estación base, lo cual es muchas veces difı́cil de obtener. Una opción ideal consiste en la conexión de todas las estaciones base a un administrador central de recursos que recibe toda la información disponible de los canales como una retroalimentación del sistema. En este esquema asumimos que toda la información de los canales está disponible para el administrador central de recursos y es una entrada al algoritmo de óptima conformación del lóbulo. Entonces, el algoritmo de óptima conformación del lóbulo intenta maximizar la SINR de cada usuario previsto. Pero cuando se colecta toda la información de los canales es inevitable que se genere un exceso de señalización. Además, se escala la complejidad de la conformación del lóbulo y el número de operaciones, y se generan más retrasos de retroalimentación entre las estaciones y el administrador central de recursos. Por otro lado, conocimiento preciso de los canales en una determinada estación base deberı́a necesitarse solamente para los usuarios que se ven fuertemente influenciados por esa especı́fica estación base. Existe también un interés creciente en trasladar la inteligencia en una red inalámbrica hacia los bordes de la red (las estaciones base). 1.1. Planteamiento del Problema El propósito de este proyecto es el desarrollo de nuevos algoritmos que resuelvan el problema de conformación del lóbulo downlink individualmente para cada celda. Puesto que la información de los canales dentro de cada celda es conocida, podemos asumir que la interferencia dentro de la celda puede ser ma- 1.2 Metodologı́a 3 nejada de manera exacta. Pero la información de los canales fuera de la celda es desconocida, por lo cual es necesario crear estrategias ad hoc para manejar la interferencia entre celdas distintas. Estas estrategias, las cuales son analizadas en el Capı́tulo 5, básicamente modifican y/o agregan restricciones al problema de conformación del lóbulo downlink usando aproximaciones para manejar la interferencia entre celdas distintas. Estos métodos son evaluados con respecto a la solución óptima conjunta, la cual se considera como el patrón ideal o benchmark. A través de la medida de la probabilidad de caı́da del servicio para cada algoritmo, nos hallamos en la capacidad de determinar la probabilidad con la cual el sistema puede cumplir con las restricciones de SINR para cada usuario. Además, debido a que el algoritmo tiene también como objetivo la minimización de la potencia usada en cualquier estación base para transmitir la señal a las estaciones móviles destino, la potencia transmitida total será considerada también como una medida de desempeño. Las principales metas del proyecto son: 1. Desarrollar nuevos algoritmos decentralizados de construcción del lóbulo en el downlink por medio de la adición y/o modificación de las restricciones del problema óptimo conjunto original, usando optimización convexa como el método para alcanzar la solución mı́nima global 2. Diseñar un ambiente de simulación donde los resultados puedan ser obtenidos a través de la promediación del desempeño del sistema en múltiples escenarios 3. Comparar las medidas de desempeño arrojadas por las simulaciones con respecto al patrón de la solución óptima y trazar conclusiones de este análisis Administración en el dominio del tiempo (scheduling) y sistemas de banda ancha están fuera del alcance de este proyecto. Esquemas de control de congestión pueden ser ejecutados como un futuro trabajo en esta área. 1.2. Metodologı́a 1.2.1. Modelo General La simulación del desempeño de los algoritmos sugeridos es efectuada en un escenario constituido como un área dividida en celdas hexagonales regulares. Con la finalidad de ignorar efectos de borde, el modelo contiene tantas celdas com sea necesario que el análisis pueda ser hecho solamente en las celdas más internas sin perder generalidad. Las estaciones bases están localizadas en el centro de cada celda y modeladas de acuerdo a un Arreglo Circular Uniforme (UCA - Uniform Circular Array) especificado en [14]. Las estaciones móviles están dispersas por todas las celdas en una distribución uniforme. La asignación a las estaciones bases es trivial (un móvil es asignado a la estación base con la que 1.2 Metodologı́a 4 mantenga el canal más fuerte). Consideramos propagación en múltiples trayectos y canales Rayleigh de atenuación plana en frecuencia. Se hace la suposición de que la atenuación rápida tiene caracterı́siticas de distribución normal mientras que la atenuación lenta tiene una distribución logarı́tmica normal. Este proyecto no estudia en profundidad cómo se calcula el ángulo de llegada de las señales interferentes, como tampoco el ángulo de la señal de interés. La información acerca de la localización en el campo está definida por la respuesta del arreglo de antenas, de acuerdo a las ecuaciones caracterı́sticas del modelo usado. Esta respuesta está directamente incluida en los vectores del canal. Debido a fines prácticos, los vectores de los canales entre las estaciones base y los móviles son generados durante las simulaciones. Se asume que el sistema es Time Division Duplex (TDD), esto quiere decir que entre las ventanas de tiempo del uplink y del downlink existe un retraso bastante corto en comparación con el tiempo de coherencia del canal. Esto permite el uso de la data del uplink (enlace de subida) para el estimado del canal downlink. 1.2.2. Algoritmo Diferentes esquemas son estudiados para resolver el problema de optimización de la construcción del lóbulo en el downlink. Es muy fácil introducir modificaciones al utilizar la solución de optimización convexa propuesta en [9]. Sin embargo, el número de variables usadas es mayor que en otras aproximaciones. Se ha comprobado que para casos donde la data del canal uplink pueda ser usada como un buen estimado del canal downlink instantáneo, el algoritmo para la óptima construcción del lóbulo descrito en [9] y [8] puede ser utilizado. Este método permite trabajar fuera del conjunto de restricciones y convertirlas en transformaciones lineales del cono convexo de segundo orden. Al hacer esto, el problema ha pasado a ser un problema de optimización convexa con restricciones de segundo orden, el cual posee varios métodos del punto interior disponibles. Tomaremos estas técnicas como un punto de partida y desde allı́ desarrollaremos nuestras propias adaptaciones de acuerdo a las limitaciones y requerimientos que encaremos en el modelo del sistema. 1.2.3. Ambiente de Simulación Se usa el paquete gratuito cvx para implementar el problema de optimización. Este software transforma a Matlab en un lenguaje de modelación, haciendo posible la escritura de restricciones y objetivos especı́ficos en sintaxis común de Matlab. Detalles acerca de este software y el interesante mundo de la optimización convexa pueden ser encontrados en [15] y [16]. SeDuMi es el único núcleo solucionador que soporta la versión de cvx que va a ser usada. Información adicional en SeDuMi es dada en [17]. Capı́tulo 2 Ambiente de Radiocomunicaciones Móviles 2.1. Modelo Celular A lo largo de los años, muchas configuraciones han sido establecidas para proporcionar el servicio de comunicación a la población de usuarios móviles, mas el modelo celular ha probado ser el más exitoso. Un ambiente radiocelular hace disponible una porción finita de espectro electromagnético o ancho de banda a lo largo y ancho de una cierta área geográfica. Esta área es dividida en pequeñas sub-áreas conocidas como celdas. Dos tipos de radiocanales son usados para la comunicación: canales de control para conducir las señales de control y canales de tráfico para conducir los mensajes. Las señales de control son empleadas para activar llamadas y manejar otras funciones de control para unidades aisladas. Los canales de tráfico llevan la voz y la data. Dependiendo de la dirección de las señales, los canales también pueden ser clasificados en downlink o forward-link (enlace de bajada o hacia adelante), que transmite desde la estación base hacia el móvil receptor, y uplink o reverse-link (enlace de subida o de regreso), que ocurre cuando el teléfono móvil pasa a ser el transmisor y la estación base es el receptor. 2.1.1. Estaciones Base Cada celda contiene una estación base, la cual está conectada a un Centro de Conmutación Telefónica (MSC - Mobile Switching Center), se comunica con los teléfonos móviles en el sitio por radioenlaces y conecta estos móviles a la Red de Telefonı́a Pública Conmutada (PSTN - Public Switching Telephone Network). Radioenlaces entre suscriptores móviles y estaciones base son establecidos usando una Interfaz Común Aérea (CAI - Common Air Interface) segura, diseñada 2.1 Modelo Celular 6 con la finalidad de mantener un protocolo de comunicación de reconocimiento mutuo (handshake). CAI provee confiabilidad en la información enviada entre el móvil y la estación base, especificando codificación de voz y de canal. La función de la estación base es la de actuar como punto central de acceso en la red para cualquier suscriptor que se encuentra de su propia celda asignada. Es el bloque de construcción básico de una red celular. Cuando una base que provee cobertura en un área limitada es interconectada con otras bases y éstas a su vez a otras, el resultado es una red inalámbrica intercontinental que cubre gran parte de la superficie habitada en el planeta. Las redes inalámbricas son altamante dinámicas en comparación con la PSTN estática, debido a que la configuración de la red es reacomodada cada vez que un suscriptor se mueve de una celda a otra. Muchos usuarios pueden solicitar servicio desde cualquier ubicación fı́sica, moviéndose a cualquier velocidad, y el MSC debe proveerles una porción de un espectro limitado de frecuencias. Para la interconexión de la mayorı́a de los MSCs, el protocolo de señalización SS7 [24] es ampliamente usado en el mundo. Por lo tanto, la complejidad de las redes de comunicación móvil obliga el uso de distintas técnicas como reúso de frecuencias, partición de celdas y filtrado en el espacio. La localización óptima de una antena que queremos sea estación base dentro de una celda no es fácil de determinar [25]. La configuración irregular del terreno causa una huella irregular de la antena a distancias tı́picas de 13 km. Además, la localización de una antena afecta al resto de las antenas debido a la interferencia. Un criterio de diseño estándar consiste en colocar la antena en un punto bajo del terreno, pero incrementamos la altura de la antena. El nivel de recepción en el borde de la celda debe ser decidido en base al número de estaciones móviles que se desea servir y el rendimiento requerido del sistema. Contornos de igual nivel mı́nimo de recepción definen el tamaño de una celda y deberı́an ser dibujados de tal manera que se minimice el solapamiento. En este proyecto asumimos un terreno plano donde las estaciones base están localizadas en un arreglo hexagonal regular. A pesar de que la huella real de una antena tiene una forma irregular como se describió antes, se necesita de una forma regular de la celda para sistematizar el diseño. Una huella circular serı́a el caso ideal, pero no podemos dibujar un mapa de cı́rculos adyacentes sin dejar espacios en blanco o solapando áreas. Si comparamos el área de un hexágono, un cuadrado y un triángulo equilátero, dadas la distancia fija entre el centro del polı́gono y el punto más lejano de su perı́metro, el hexágono posee el mayor área de los tres. Ası́, los hexágonos se aproximan muy cercanamente al patrón de radiación circular ideal de una antena omnidireccional en un escenario de propagación en el espacio libre. La estación base consiste tı́picamente de un arreglo de antenas transmisoras y receptoras que manejan simultáneamente comunicaciones full duplex. Detalles en las caracterı́sticas de este arreglo serán dadas en el capı́tulo 3. 2.1 Modelo Celular 2.1.2. 7 Estaciones móviles El término móvil se ha referido tradicionalmente a todo aquél dispositivo de transmisión/recepción que es susceptible de ser desplazado durante la operación. En ciertas ocasiones se hace la distinción entre móvil (terminal de radio transportado en un objeto moviéndose a alta velocidad, por ejemplo a un vehı́culo) y portable (terminal de radio transportado por un usuario moviéndose a la velocidad del paso normal), mas en este proyecto no los diferenciaremos y llamaremos a ambos como estaciones móviles. También podemos llamarlos suscriptores, puesto que cada usuario paga una tarifa de suscripción para accesar al sistema. En algunos escenarios donde es importante analizar cómo es manejado el tráfico, se utiliza el modelo de Poisson para describir las llegadas de los nuevos usuarios al sistema telefónico, asumiendo que la población es infinita. Para poblaciones finitas, el modelo Bernoulli es comúnmente usado. Estos esquemas no serán discutidos en el proyecto. 2.1.3. Reutilización de frecuencias El espectro electromagnético es limitado en cualquier área, por lo que debe ser usado sabiamente por los sistemas de comunicación. Entonces, una de las razones fundamentales por las que el diseño celular es usado, es por la posibilidad de administrar el conjunto disponible de frecuencias y ubicarlas en una manera tal que la interferencia co-canal es minimizada. Comúnmente, las celdas son arregladas en clusters. Un cluster es un grupo de celdas que colectivamente usan el conjunto completo de frecuencias disponibles [1]. En estos sistemas, la capacidad es dada por C = M kN = M S (2.1) Donde S es el número total de canales duplex disponibles para su uso, k es el grupo de canales fijos para cada celda, N es el tamaño de los clusters y M es el número de veces que un cluster es replicado en el área de cobertura. Si se reduce el tamaño del cluster mientras se mantiene constante el radio de la celda, se necesitarán más clusters para cubrir el mismo área. Ésto incrementa la capacidad del sistema, pero también produce que las celdas co-canales estén localizadas mucho más cercanas unas de otras. Una fórmula comúnmente usada para agrupar las celdas por todo el espacio es D= √ 3NR (2.2) Donde D es la distancia entre las celdas co-canales y R es el radio de la celda. En el caso de tener varios usuarios compartiendo el mismo canal dentro de la misma celda, el cual es el caso de este proyecto, el factor de reutilización es mayor que 1. A esta operación se le llama a menudo Acceso Múltiple por División Espacial (SDMA - Space Division Multiple Access). 2.2 Ruido e interferencia 2.1.4. 8 Partición de celdas El radio de la celda en los sistemas celulares tempranos podı́a llegar a medir varios kilómetros. Estos sistemas se conocen hoy como sistemas macrocelulares o macroceldas. La penetración del mercado a lo largo de los años incrementó el número de usuarios por unidad de área, lo cual requerı́a de mayor porción de espectro libre. Por consiguiente, los sistemas se actualizaron de la siguiente manera: se disminuyó la potencia de la antena, el radio de la celda fue acortado, más canales estuvieron libres en áreas pequeñas y entonces se pudo aumentar la capacidad. No obstante, los sistemas actuales no son uniformes, lo cual significa que en áreas particulares dentro de una celda se puede concentrar una desproporcionada cantidad de usuarios, generando un desbalance. Esta situación se resuelve al hacer particiones de las celdas, o cell splitting. Una celda se puede dividir en varias porciones conocidas como microceldas, con estaciones base muy cercanas una de la otra. En escenarios de aún mayor demanda, tales como áreas públicas llenas de individuos, los pisos de un edificio de oficinas, etc. el espectro puede ser reubicado a un área todavı́a menor, llamada picocelda. 2.1.5. Hand-Off Se denomina hand-off a la serie de estrategias implementadas por el sistema de comunicación móvil cuando un usuario se desplaza de una celda a otra. Es una de las más importantes tareas de cualquier sistema celular: incluso existen sistemas donde las peticiones de hand-off tienen prioridad sobre las de iniciación de llamada. Cuando el usuario entra en una celda, la polı́tica de hand-off requiere que la nueva estación base sea identificada y las señales de voz y control sean asignadas a esta base. El umbral de hand-off debe ser ligeramente mayor que el mı́nimo nivel de señal usable. Las polı́ticas de hand-off persiguen el mantenimiento de calidad de diálogo y audición a lo largo del proceso de llamada, ası́ como la preservación del concepto de la red celular planificada, evitando congestiones y prohibiendo el uso de canales fuera de la celda a la cual fueron asignados. Un modelo analı́tico para tráfico y hand-off fue estudiado en [26] y [27]. En este proyecto se asume que, si bien los móviles están en movimiento y para ello se contabiliza el desvanecimiento rápido, sus desplazamientos nunca son de larga distancia y no habrá situaciones donde un usuario sea transferido de una celda a otra. 2.2. Ruido e interferencia Además de las pérdidas por el camino de propagación y desvanecimiento en múltiples trayectorias (aspectos discutidos en el capı́tulo 4), las comunicaciones inalámbricas son afectadas por niveles de ruido e interferencia. Es interesante notar que los algoritmos de conformación del lóbulo responden al ruido en diferente manera que a la interferencia. El nivel de ruido del sistema puede es- 2.2 Ruido e interferencia 9 calar la potencia del vector que contiene los pesos, mientras que la interferencia producirá una respuesta de cero forzado en dirección de la señal interferente. 2.2.1. Medios Limitados por Ruido, Medios Limitados por Interferencia Un enlace de radiocomunicación entre dos unidades transceptoras se encuentra afectado por ruido termal. Si una de las unidades está en movimiento, el desempeño también es afectado por la atenuación en múltiples trayectos. Se dice que los medios de este tipo se llaman medios limitados por ruido. Cuando varias unidades transceptoras ocupan posiciones cercanas dentro de un mismo espacio usando canales de la misma frecuencia o canales adyacentes (los vecinos inmediatos inferior o superior), y la potencia de esta interferencia es superior a la potencia del ruido, estamos ante la presencia de un medio limitado por interferencia. 2.2.2. Interferencia Celular Podemos clasificar a la interferencia dependiendo de su fuente. Dada la estación base k a la cual se encuentra asignado el subconjunto de móviles I(k), donde un móvil i está asignado a k y es parte de I(k). La interferencia interna de la celda en i es la suma de las señales que k envı́a a otros usuarios co-canales pertenecientes a la misma celda I(k), siendo recibida por i. La interferencia hacia otras celdas es la suma de señales de usuarios co-canales fuera de I(k). Esta notación será usada en el resto del proyecto. 2.2.3. Razón de Señal a Interferencia más Ruido La Razón de Señal a Interferencia más Ruido (SINR - Signal to Interference Plus Noise Ratio) es sin lugar a dudas el más importante de los parámetros de desempeño. De hecho, la mayorı́a de los algoritmos para la alocación de recursos radiocelulares que han sido desarrollados para hand-off, asignación dinámica de canales, control de potencia y construcción del lóbulo (incluidas las propuestas de este proyecto), son tomados con la presunción de que los suscriptores y/o las estaciones base (BSs) tienen acceso a mediciones en tiempo real de la SINR recibida. De cualquier modo, medidas SINR en servicio dependen fuertemente en cómo se configura el sistema, lo cual es a menudo confidencial. Capı́tulo 3 Arreglo de Antenas Transmisoras Las antenas isotrópicas irradian igual cantidad de potencia en todas las direcciones, originando que las señales puedan ser detectadas con la misma intensidad en un área de cobertura de la forma de un cı́rculo suave, si el terreno es perfectamente plano. Debido a los obstáculos e imperfecciones a nivel del suelo, el área de cobertura adopta una forma irregular, intensificando la potencia recibida en algunos puntos y produciendo interferencia indeseada en otros. Además, si algunas áreas necesitan mayor potencia que otras, debemos tener en cuenta que la potencia en una sola antena isotrópica no puede ser aumentada indiscriminadamente, debido a limitaciones de energı́a y a la interferencia producida en direcciones indeseadas. La actual demanda para mejores técnicas de transmisión ha obligado el desarrollo de nuevas antenas y mecanismos que representan una alternativa al uso de antenas omnidireccionales aisladas. Este es el caso de las antenas direccionales, las cuales proveen una dirección en la cual la antena tiene una máxima ganancia. Podemos emular esta directividad a través de arreglos de antenas, donde se le proporciona el peso y fase apropiados a la señal de cada elemento del arreglo, combinando las señales y produciendo una salida única. El lóbulo principal puede ser apuntado en diferentes direcciones, dándole la posibilidad a sistemas adaptivos de responder a la alta movilidad y volumen de las comunicaciones de hoy en dı́a. En caso de antenas adaptivas, la ganancia y la fase inducidas en los diversos elementos son cambiadas antes de la combinación lineal de las señales, para ası́ ajustar la ganancia del arreglo en una manera dinámica tal y como sea requerido por el sistema. Además de estos beneficios en ganancia, directividad y adaptibilidad, las ventajas de los arreglos o arrays de antenas van más allá, ya que permiten la identificación, selección y representación de señales en ambientes complejos como comunicaciones móviles, radar y otras aplicaciones. Los arreglos de antenas permanecen como un tópico caliente para la investigación. Desarrollos en arreglos conformales y arquitecturas de microstrip 3.1 Modelo de Arreglo de Antenna 11 Figura 3.1: Transmisión desde una estación móvil a una estación base en un ambiente urbano. La estación base sigue el modelo ACU. Dispersión en torno al móvil crea un ángulo de dispersión σθ en la señal proveniente del ángulo θ pudieran poner en marcha la implementación de arreglo de antenas receptoras en los dispositivos móviles, lo cual permitirı́a el empleo de comunicaciones celulares MIMO (Multiple Input Multiple Output - Múltiples Entradas Múltiples Salidas). Información adicional en técnicas de implementación, arquitecturas y modelos pueden ser encontradas en [22] y [18]. 3.1. Modelo de Arreglo de Antenna La geometrı́a de arreglo de antenas que vamos a usar en este proyecto es la de Arreglo Circular Uniforme (ACU) Un ejemplo simple puede ser visto en 3.1. Arreglos circulares son usados en aplicaciones que requieren cobertura completa en todos los azimut. Se asume que los m elementos de antena son omnidireccionales. Siendo este un modelo práctico, el arreglo está compuesto de un número finito de elementos, además son sólo una aproximación de una apertura circular continua ideal. En consecuencia, podemos observar oscilaciones en fase y amplitud, que sólo pueden ser reducidas a un nivel aceptable si el radio del arreglo es calculado para que alcance un espacio entre los elementos apenas por debajo de λ2 . La respuesta del array, a(θ) para la ACU, con una señal viniendo de un punto lejano con ángulo θ se encuentra expresada en la siguiente ecuación: m−1 2πα 2πα a(θ) = ej λ cos(−θ) . . . ej λ cos( m 2π−θ) (3.1) Este modelo se encuentra en [14], y se basa en la determinación de la dirección a través del estı́mulo. Su simplicidad y sensitividad es considerablemente grande. Uno de sus aspectos más particulares es que, en contraste con arreglos 3.2 Construcción del lóbulo 12 lineales, la dirección en la que apunta el lóbulo generado no es dependiente de la frecuencia, aunque el uso de desplazadores de fase hace que el ancho del lóbulo sea en pequeña magnitud dependiente de la frecuencia. En [19] podemos encontrar un trabajo de cómo lidiar con el problema de construcción del lóbulo para arreglos circulares en escenarios de amplio espectro. Los arreglos de antenas pueden encontrarse en ambos extremos del radioenlace, pero en este proyecto consideramos que solamente la estación base cuenta con arreglo de antenas. Se asume que la estación móvil tiene una sola antena omnidireccional. Existe solamente un arreglo por celda. Usamos aproximación de campo y de banda estrecha. Por ello podemos decir que las distancias entre la estación base y todas sus estaciones móviles asignadas a su celda son mucho mayores que la distancia entre los elementos de la antena, haciendo que todas las ondas que llegan al arreglo sean planas. Además, el ancho de banda del equivalente en banda base de las señales recibidas de y transmitidas hacia los usuarios es considerado mucho menor que el recı́proco del tiempo máximo que una onda de radio plana con velocidad de propagación co necesita en cubrir el diámetro del arreglo de antenas. 3.2. Construcción del lóbulo La construcción del lóbulo o beamforming es el proceso en el cual damos peso apropiado (en amplitud y fase) a las señales en un arreglo de antenas y a través de la combinación de estas señales podemos fortalecer la salida deseada, mientras se filtran las interferencias no deseadas y el sonido ambiental y propio del sistema [4]. Es aplicable tanto a radiación como recepción de energı́a. El lóbulo apunta hacia la dirección en la cual el arreglo tiene respuesta máxima y por lo tanto, máxima ganancia. Generalmente la construcción del lóbulo incluye la formación de los patrones de radiación y técnicas de combinación de diversidad espacial. La construcción del lóbulo para arreglos adaptivos puede ser dependiente de la señal fuente o construidos como un proceso estatı́sticamente óptimo. Dicho método es capaz de proveer mejor recepción de señal cuando se compara con el arreglo sintetizado, el cual siempre posee un conjunto de pesos fijos que produce una respuesta del arreglo fija que puede ser conmutada entre un determinado grupo de direcciones [34]. El patrón de radiación es el dibujo en el plano de la respuesta del arreglo como función del ángulo. En cualquier patrón de radiación podemos observar una serie de mı́nimos y máximos. El lugar donde el patrón de radiación cae a un valor muy pequeño es normalmente referido como un cero (null). La porción del patrón que se ubica entre dos ceros y consigue su máxima ganancia es normalmente referida como lóbulo principal. El ancho del lóbulo principal es por lo general medido en los puntos de media potencia. Pero también pueden encontrarse lóbulos laterales o secundarios a cualquier lado del lóbulo principal, con mı́nimos locales. En un arreglo de m elementos se pueden especificar m − 1 posiciones o grados de libertad del arreglo. Si el número de los elementos del arreglo es pequeño, entonces al colocar 3.2 Construcción del lóbulo 13 un cero para suprimir una señal interferente, se puede substancialmente afectar la sensitividad del arreglo. Al incremenar el número de los elementos podemos obtener resoluciones más altas, pero el costo y complejidad del arreglo también crece. Por ello es que en todo diseño, el ingeniero debe jugar con la resolución del array, el nivel de los lóbulos laterales y el número de elementos de antena. En el caso de este proyecto, se escoge un número pequeño de elementos de antena más que todo debido a capacidad de cómputo limitada. En un principio, la construcción del lóbulo como proceso puede ser aplicada tanto en el uplink como en el downlink, sin embargo existen algunas diferencias conceptuales. En el caso del uplink, el lóbulo puede ser construido independientemente en cada receptor, sin alterar directamente el estado de los otros enlaces, mientras que en el downlink la construcción del lóbulo en un transmisor producirá interferencia en todos los receptores. Ası́ que, al diseñar los beamformers o vectores conformadores del downlink, debemos preocuparnos por la ganancia total del sistema en lugar del enlace individual, porque los distintos beamformers de un sistema afectan de manera conjunta el desempeño global. 3.2.1. Uplink Beamforming Los arreglos de antenas ayudan a la identificación y selección de las señales uplink provenientes de diferentes usuarios, a la vez que disminuyen los requerimientos del lazo de control de la potencia y se mitiga el impacto de las inexactitudes de dicho lazo. La literatura es extensiva sobre algoritmos para encontrar los uplink beamformers, por ejemplo [4], [22] y [23]. Para el caso uplink se asume conocimiento total de la respuesta impulsiva del canal. Esto es posible ya que el canal puede ser estimado durante la recepción. La mayorı́a de las soluciones toman cierta asignación de potencia predeterminada y calculan el uplink beamformer que maximice la SINR por descomposición de los autovalores independientes. En técnicas óptimas, se formula una función costo tal que cuando ésta sea minimizada, la calidad de la señal a la salida del arreglo es maximizada. Las soluciones pueden ser encontradas a través de la aplicación de los criterios de la Media Cuadrada Mı́nima (MMSE - Minimum Mean Square Error) o de los Mı́nimos Cuadrados (LS - Least Squares). 3.2.2. Downlink Beamforming Como se ha mencionado anteriormente, el downlink es una de las partes más crı́ticas de la comunicación, no sólo debido a que la construcción del lóbulo en el transmisor afecta a todos los usuarios dentro de la celda sino por la asimetrı́a en el tráfico de datos, lo cual conduce a un cuello de botella en la capacidad de comunicación entre la estación base y los terminales. Mejoras en el desempeño en el downlink pueden ser implementadas si permitimos al suscriptor del otro lado del enlace a usar procesamiento espacial. No obstante, debido a espacio, potencia y cómputo limitados, las unidades móviles tı́picamente sólo cuentan con un solo elemento de antena y pueden realizar un procesamiento espacial muy limitado. De todas formas, es razonable suponer 3.2 Construcción del lóbulo 14 que la estación base sı́ cuenta con un arreglo de antenas. En consecuencia, ese es el esquema que usaremos en este proyecto: arreglo de antenas en el punto de acceso y una antena simple en los terminales. La principal dificultad en el downlink beamforming es que, con la finalidad de formar lóbulos eficientes en la celda, el canal entre las estaciones móviles y las estaciones base debe ser conocido antes de la transmisión, mientras que en el uplink el canal puede ser estimado durante la recepción. El canal es más complejo, como también son complejos los algoritmos para estimarlo. También, la otra complicación importante en el downlink beamforming es la limitación en la potencia que podemos usar. Cuando la ganancia del arreglo de antenas se incrementa hacia una dirección en especı́fico para satisfacer los requerimientos de algún usuario, la potencia total transmitida debe ser restringida. Si no fuese ası́, la excesiva ganancia en una dirección podrı́a empeorar la CCI dentro y fuera de la celda. Además debemos recordar el hecho de que nuestro transmisor puede manejar un nivel de potencia dentro de unos ciertos rangos. Capı́tulo 4 Modelo del canal Un canal es un enlace conectando a un transmisor y un receptor en un sistema de comunicaciones. Como cualquier otro medio fı́sico, los canales de comunicación están sujetos a atenuación. En el espacio libre, las razones de pérdidas por propagación dependen únicamente de la frecuencia de la señal transmitida y la distancia entre el transmisor y el receptor. Puesto que las señales con las cuales estamos trabajando en este proyecto son básicamente señales para móviles a nivel del terreno, debemos usar un modelo para la comunicación móvil a nivel del suelo, afectada no sólamente por las longitudes de onda de las frecuencias en las que se propaga, sino también por la posición de estructuras hechas por el hombre y la propia naturaleza móvil del receptor. También, los sistemas de banda estrecha, tales como los de primera generación de telefonı́a celular, son afectados por la rápida variación espacial debido a la interferencia entre múltiples trayectorias de llegada. En este capı́tulo damos una explicación detallada de los modelos estadı́sticos usados para determinar los canales de comunicación usados durante la simulación. 4.1. Propagación en Múltiples Trayectorias En los sistemas inalámbricos modernos, los radioenlaces cubren distancias relativamente cortas, lo cual permite la implementación de reutilización de frecuencias y baja potencia irradiada por las antenas. Considerando lo corto de estas distancias y debido al hecho de que la mayorı́a de las unidades móviles se encuentran dentro de áreas urbanas, los problemas de propagación más graves se originan por obstáculos como edificios y estructuras construidas. En esos ambientes, lı́nea directa de vista entre la estación base y la antena de la unidad móvil es bien difı́cil. Por lo contrario, los edificios actúan como dispersores y la señal puede difractarse en torno a ellos (en ciudades donde las antenas están considerablemente por debajo del techo de los edificios), sobre ellos (edificios de media y baja altura) o ambos (edificios de altura mixta). La dispersión produce que dos o más versiones atenuadas de la misma señal transmitida puedan 4.2 Desvanecimiento 16 alcanzar a la antena receptora a través de distintos caminos desde distintas direcciones de arribo. La diferencia entre las longitudes de trayectoria de las ondas de radio entrantes genera un retraso diferencial en el tiempo que introduce un cambio de fase entre las componentes de la señal. Estas componentes son sumadas constructiva o destructivamente. En consecuencia, los efectos de la propagación en múltiples trayectorias pueden ser vistos como una ganancia de trayecto. Por principio de reciprocidad, la ganancia de trayecto es la misma no importa si el transmisor está ubicado en la estación base y el receptor en el móvil o viceversa, si decimos que la transmisión es a la misma frecuencia (en realidad hay una diferencia). Si también consideramos un móvil receptor viajando a una velocidad constante, la longitud del trayecto cambiará de acuerdo a su posición y el impacto de las diferentes componentes entrantes será variante en el tiempo. La amplitud de la señal recibida fluctuará y en algunos puntos habrá alta adición constructiva y en otros casi absoluta cancelación. Este fenómeno es denominado fading o desvanecimiento y será detallado en la siguiente sección. Puede existir una modulación de frecuencia aleatoria debido a los variantes desplazamientos doppler en las diferentes señales multi-trayectos. La dispersión Doppler de la señal recibida incrementa el ancho de banda de la señal. El espectro de densidad de potencia del delay o retraso describe la intensidad del proceso de dispersión promediada a un determinado retraso en la propagación. Podemos tomar dos momentos estatı́sticos de esta función y usarlos para nuestro propio interés y ellos son el delay spread o dispersión de retardo y el Doppler spread o dispersión Doppler. El delay spread aparece porque el móvil recibe varias copias retrasadas de la misma transmisión generando una dispersión de la señal en el tiempo. Valores tı́picos de la dispersión del retardo abarcan desde una fracción de microsegundo en áreas urbanas a valores del orden de los 100 segundos en un área con colinas, lo cual restringe el máximo ancho de banda de la señal entre 40 y 250 kHz [2]. El inverso del delay spread se define como ancho de banda de coherencia del canal, denotado por Bc . De la misma manera, el inverso de la dispersión Doppler es una medida del tiempo de coherencia del canal, el cual es denotado por τc . Estos dos parámetros caracterizan la naturaleza del canal. En este proyecto asumiremos canales de comunicación planos en frecuencia, ya que en transmisiones de radio móviles el ancho de banda del mensaje es muy pequeño en comparación con el ancho de banda de coherencia del canal. 4.2. Desvanecimiento El desvanecimiento es usado para describir fluctuaciones en amplitud, fase y retrasos multi-trayecto de una radioseñal en un corto perı́odo de tiempo o corta distancia de recorrido. Es causado por la propagación multitrayectoria explicada en la sección previa. El desvanecimiento es altamente dependiente a la relación entre los parámetros de la señal (tales como ancho de banda, perı́odo intersimbólico, etc.) y los parámetros del canal (tales como dispersión de retardo y dispersión Doppler). Estudiamos solamente los casos que nos conciernen en 4.3 Modelo de Canal de Banda Estrecha 17 este modelo: desvanecimiento a gran escala y desvanecimiento a pequeña escala. 4.2.1. Desvanecimiento a gran escala El desvanecimiento a gran escala es causado principalmente por la configuración del terreno y representa el promedio de las pérdidas producidas por el movimiento sobre amplias áreas. A menudo se dice que el receptor es ocultado por prominentes contornos del terreno como colinas, bosques, vallas publicitarias o grupos de edificios en el trayecto entre el transmitor y el receptor. Las estadı́sticas del desvanecimento a gran escala usadas en ete proyecto son descritas en términos de la media de pérdidas por trayecto, proporcional a r1α (donde r es la distancia entre la estación base y la estación móvil, y α es el coeficiente de pérdidas, por lo general en el rango 2 ≤ α ≤ 4), y una variación de distribución log-normal alrededor de la media (con varianza σsf ). 4.2.2. Desvanecimiento a pequeña escala El desvanecimiento a pequeña escala causa rápidos cambios en la respuesta impulsiva del canal en el intervalo de un sı́mbolo y es causado por reflexión multi-trayectos de la onda transmitida por dispersores locales. Si la lı́nea de vista entre transmisor y receptor es obstruida, la envolvente de la señal recibida se comporta como una distribución Rayleigh. Entonces se dice que el canal es un Canal de Desvanecimiento Rayleigh. En caso contrario, si existen dispersores fijos y el trayecto de propagación principal es lo suficientemente fuerte, el modelo Rayleigh pasa a ser inexacto y una distribución Rician serı́a más apropiada. 4.3. Modelo de Canal de Banda Estrecha Un canal de radiocomunicaciones móviles puede ser modelado como un filtro lineal con una respuesta impulsiva variante en el tiempo, donde la variación en el tiempo es dada por la cambiante posición espacial del móvil. Daremos primero un modelo simple con una única señal transmitida de una estación base a una estación móvil. Usando la notación en [28] y [8], la señal pasabanda transmitida puede ser representada como s(t) = Re s̃(t)ej2πfc t (4.1) Donde s̃(t) es la envolvente pasabajo compleja de la señal transmitida y fc es la frecuencia de la portadora. Debido a efectos multitrayecto mencionados en la sección previa, el canal tiene una respuesta impulsiva variante en el tiempo y dependiente del retraso, cuya función puede expresarse como h(τ ; t) = Re h̃(τ ; t)ej2πfc t (4.2) h̃(t) es la respuesta impulsiva pasabajo compleja del canal y τ es la variable del 4.4 Múltiples usuarios y múltiples antenas 18 retraso. Asumimos que la señal multi-trayecto recibida en el tiempo t consiste en la suma de componentes que han seguido L diferentes trayectos, donde L es muy grande debido a reflexiones, difracciones y dispersiones en las cercanı́as del móvil. Tı́picamente, los dispersores no están correlacionados y entonces la función h̃(t) puede ser modelada como un proceso Gaussiano de media cero y valores complejos. El canal será llamado de ahora en adelante canal de desvanecimiento Rayleigh. La señal recibida, para t > 0 será: ∞ h(τ ; t)s(t − τ )dτ + n(t) (4.3) r(t) = 0 Aquı́, n(t) es el ruido blanco aditivo Gaussiano con distribución N (0, σ 2 ). En las radiotransmisiones móviles tı́picas, el ancho de banda de la señal es muy pequeño en comparación con el recı́proco de la dispersión de los retardos multi-trayectos. Por ende, podemos asumir que no hay dispersión en el tiempo y h(τ ; t) = 0 para τ = 0. Basado en el teorema Nyquist-Shannon, la señal discreta recibida es entonces r(t) = h(t)s(t) + n(t), t > 0 (4.4) Aun cuando usaremos representación de banda estrecha en este proyecto, las señales reales con señalización digital pueden ocupar un ancho de banda mucho más amplio. 4.4. Múltiples usuarios y múltiples antenas Si el modelo es extendido a un ambiente de comunicación móvil celular con K estaciones base compuestas de m elementos de antena llevando a cabo una transmisión sincronizada a d móviles compartiendo los mismos recursos de espectro, la señal banda base ri (t) recibida en el móvil i está dada por ri (t) = K h∗i,k xk (t) + ni (t) (4.5) k=1 En este caso, xk (t) es el vector de señales transmitidas por los elementos de antena en la estación base k y hi,k ∈ Cm es el vector del canal entre la estación base k y el móvil i. El vector xk (t) es determinado por xk (t) = wi si (t) (4.6) i∈I(k) wi ∈ Cm es el vector de beamforming que proporciona el peso apropiado a la señal modulada si (t) dirigida al móvil i. Asumiremos en el resto del proyecto que si 2 = 1. Entonces, la potencia de transmisión downlink estará definida 4.5 Estimación del Canal Downlink 19 por los vectores conformadores del lóbulo. Para aclarar este concepto, podemos expresar al vector conformador de downlink como wi = √ pi ui (4.7) Donde pi es un escalar que provee el peso apropiado al filtro espacial normalizado ui de longitud m. De la misma manera, el conformador uplink puede √ expresarse como wi = q i ui , sin perder generalidad. Los algoritmos de conformación del lóbulo en el downlink que usamos en este proyecto determinarán tanto el control de potencia como el filtrado espacial de manera conjunta. No obstante, se han desarrollado algunas soluciones han sido desarrolladas que separan estos procedimientos, y después que los vectores ui son encontrados, un esquema estándar de control de potencia es aplicado. Lectura adicional en este método de convergencia puede verse en [8]. Cuando decimos que el móvil i pertenece a I(k), especificamos que el móvil se encuentra asignado a la estación base k. De ahora en adelante, la notación I(k) es usada para aquellos usuarios que están localizados dentro de la misma celda. Igualmente, κ(i) se refiere a la estación base asignada al móvil i. Una estación móvil puede ser asignada a una sola estación base a la vez, debido a que no consideramos situaciones de handover suave. 4.5. Estimación del Canal Downlink Dadas todas las premisas que hemos mencionado hasta aquı́ y aplicando el conocimiento que poseemos de propagación multi-trayectos y desvanecimiento, podemos expresar la fórmula para el canal uplink de desvanecimiento Rayleigh como la suma de los L trayectos reflejados de una onda plana con frecuencia f proveniente de una fuente localizada en un ángulo θ(t) cambiante en el tiempo (puesto que la fuente es móvil). La onda llega al arreglo de antenas determinado definiendo una respuesta del arreglo a(θ; f ). Se supone que el arreglo está calibrado y que las condiciones para el downlink son las mismas que para el uplink. Es posible escribir el vector del canal uplink de una estación móvil a una estación base como hup = L γlup a(θlup ; f up ) (4.8) l=1 Aquı́, γlup es el coeficiente de amplitud compleja para cada trayecto. La respuesta del arreglo es definida de acuerdo con su topologı́a. En este proyecto utilizamos la expresión formulada en (3.1). Para el caso downlink tenemos hdown = L l=1 γldown a(θldown ; f down ) (4.9) 4.6 Retroalimentación 20 En sistemas Time Division Duplex (TDD - División de Tiempo Duplex), las transmisiones uplink y downlink comparten la misma frecuencia usando diferentes ventanas de tiempo. Si el retraso entre las ventanas de tiempo del uplink y del downlink es pequeño en comparación con τc (tiempo de coherencia del canal), la huella del downlink es idéntica por reciprocidad a la del uplink. En este caso, podemos asumir que θlup = θldown y γlup = γldown, ası́ que el canal uplink instantáneo puede ser usado como un buen estimado del canal downlink. De ahı́ que la matriz de correlación Ri,k = hi,k h∗i,k tenga rango unitario. Cuando la separación duplex es mayor que el tiempo de coherencia del canal no podemos efectuar caracterización instantánea del canal, pero aún es razonable asumir θlup = θldown y E[|γlup |2 ] = E[|γldown |2 ]. Ası́, tenemos acceso a la matriz de rango completo de correlación del canal Ri,k = E[hi,k h∗i,k ]. Es conveniente expresar Ri,k como inversamente proporcional al cuadrado de la distancia entre el móvil y la base y proporcional a la matriz de covarianza Ra (θ). Una ecuación para la matriz Ra (θ) de tamaño k, l en un arreglo circular uniforme fue presentada en [29] y es dada por j Ra ACU ,kl (θ) = e 4πα λ k+l−2 sin(π k−l −θ) − n ) sin(π n e 2 σa 2 k−l k+l−2 ( 4πα −θ) λ sin(π n ) cos(π n (4.10) Ya que los dispersores están esparcidos por el terreno, las señales reflejadas desde el móvil llegan a la estación base en ángulos que están distribuidos de manera gaussiana alrededor de la lı́nea de vista directa entre el transmisor y el receptor. Este efecto dispersor puede ser modelado a través de una dispersión angular con una varianza relativamente pequeña σa2 . En sistemas Frequency Division Duplex (FDD - División de Frecuencia Duplex), la brecha de frecuencia entre el up y downlink a menudo sobrepasa el ancho de banda de coherencia Bc del canal y por lo tanto, los canales uplink se desvanecen independientemente de los canales downlink. Si consideramos la matriz de covarianza del canal como promediada sobre el desvanecimiento rápido, podemos seguir obteniendo buen rendimiento. De cualquier modo, existen muchas más estrategias sofisticadas para la estimación del canal, las cuales usan data de entrenamiento, retroalimentación desde el móvil, método Capon, etc. 4.6. Retroalimentación Los canales de control en sistemas de comunicación se encuentran disponibles para la implementación de control de potencia, modulación adaptiva y algunos modos de diversidad a lazo cerrado. Partiendo de este hecho, el transmisor puede aprovechar la retroalimentación desde el receptor para explotar las condiciones del canal y evitar interferencia. Sin embargo, es usual que la retroalimentación esté severamente limitada, ası́ que es importante determinar cómo cuantizar la información necesitada en el transmisor y en qué medida se beneficiará el desempeño del sistema a partir de la cantidad de información retroalimentada recibida. 4.6 Retroalimentación 21 Una estrategia de retroalimentación entre la estación base y el terminal en un sistema de comunicaciones comienza cuando la estación base transmite una secuencia piloto a la estación móvil. El móvil receptor usa esta secuencia para calcular la información retroalimentada. Esta información es inmediatamente enviada de vuelta a la estación base. Entonces, la estación base usa la información para estimar algunos parámetros de Calidad de Servicio (QoS - Quality of Service), por ejemplo la Razón de Señal a Ruido (SNR - Signal to Noise Ratio), los cuales serán las variables de entrada del problema de optimización de la conformación del lóbulo en el downlink. Seguidamente, la estación base escoge una tasa de transmisión capaz de satisfacer la capacidad definida por la probabilidad de caı́da del servicio (dada una estimación SNR y sus estadı́sticas). Finalmente, la estación base usa los restantes tiempos de sı́mbolo para la transmisión de data. El receptor fija su propio conformador uplink tal que su estimación SNR sea maximizada. Algunos métodos alternativos de estimación del canal toman ventaja de las estrategias de retroalimentación de código espacio-tiempo, las cuales fueron mostradas en [32] y [33], las cuales prueban que la Información de Estado del Canal (CSI - Channel State Information) puede ser cuantizada y enviada al transmisor sobre un canal de retrolamientación con tasa limitada, aunque se pierde algo de estructura propia. Este proyecto no usará diversidad transmisora y consideraremos al canal downlink como inferido del canal uplink. Sin embargo, algunos parámetros especiales para la señal recibida en el móvil pueden ser enviados de vuelta a la estación base, tales como estadı́sticas de la potencia de la señal, interferencia y mediciones de calidad. Capı́tulo 5 Algoritmos de Conformación del Lóbulo en el Downlink Como ha sido dicho antes en este reporte, la literatura acerca de conformación del lóbulo para el caso del uplink es extensa, cuyos ejemplos podemos encontrar en [3, 4, 20, 22, 23, 30]. Sin embargo, la conformación del lóbulo para el downlink no ha sido tan ampliamente investigado. En [5], la conformación del lóbulo para el downlink en escenarios multiusuarios es formulada como un problema de optimización donde los vectores peso para las distintas estaciones móviles son optimizados de manera conjunta con la finalidad de satisfacer determinadas especificaciones de umbral SINR en cada móvil, mientras se minimiza el total de potencia transmitida desde la estación base. Este es un problema cuadrático de optimización con restricciones cuadráticas no convexas. Diferentes soluciones han sido presentadas (ver [8] para un vistazo general). El problema fue resuelto por primera vez por Rashid-Farrokhi et.al. [6] quienes presentaron una generalización del algoritmo de control de potencia que logra un conjunto de vectores conformadores transmisores óptimos y viables, si acaso existe la solución. Varias soluciones basadas en la dualidad entre canales uplink y downlink han sido construidas para obtener de manera iterativa los vectores conformadores en el downlink. Algunos resultados pueden ser encontrados en [10], [11] and [12]. Sin embargo, el comportamiento de convergencia de estos algoritmos se hace más lento a medida que los requerimientos de SINR se hacen más estrictos. Una estrategia de transmisión fue especificada en [9], donde se demostró cómo el problema de optimización puede ser relajado usando programación semidefinida y aún ası́ ser capaces de seguir obteniendo la solución óptima. Este procedimiento fue adaptado en [13] donde los vectores conformadores de diferentes estaciones móviles son optimizados conjuntamente en sus correspondientes subespacios, en lugar de buscar a través de todo el espacio de parámetros. 5.1 Conformación óptima del lóbulo 23 Los algoritmos de asignación de recursos mencionados en el párrafo anterior requieren conocimiento global de las estadı́sticas del canal y pueden ser usados en la búsqueda de lı́mites fundamentales de desempeño en un sistema inalámbrico. Para disminuir la señalización entre las estaciones base, reducir el número de operaciones y decentralizar la solución del problema, hemos desarrollado nuevas técnicas con retroalimentación reducida desde el móvil. Solamente se requiere que las estaciones base tengan acceso a la información de los canales dentro de sus propias celdas y encontrar soluciones prácticas a sus usuarios asignados. 5.1. Conformación óptima del lóbulo Existen muchas maneras de definir conformación óptima del lóbulo. Nos adherimos al esquema propuesta en [5], basado en la perspectiva del operador. El sistema debe proveer una cierta Calidad de Servicio (QoS) a cuantos usuarios sea posible manteniendo un bajo costo. Se asume que los requerimientos de QoS son satisfechos si la SINR en el terminal i excede el umbral γi . Vale la pena notar que diferentes usuarios pueden demandar diferentes requerimientos de QoS, dependiendo de los recursos que necesiten. Ası́, un sistema debe ser capaz de satisfacer diferentes umbrales de SINR a cada usuario. De (4.5) y (4.6) podemos derivar una expresión más completa de la señal recibida como h∗i,κ(n) wn sn (t) + ni (t) (5.1) ri (t) = h∗i,κ(i) wi si (t) + n=i señal deseada ruido interferencia Como puede verse, la estación base κ(i) modula la señal si (t), le da un peso apropiado wi (t) para cada elemento de antena y entonces transmite a través del canal hi,κ(i) . Pero esta señal es afectada por la transmisión paralela de otras señales dirigidas a otros usuarios a través de los canales existentes entre todas las estaciones base y el móvil i. Si queremos que la SINR en este móvil sobrepase la restricción γi , y asumiendo que las estaciones base transmiten cada sı́mbolo simultáneamente en sincronización, entonces el sistema debe cumplir la expresión wi∗ Ri,κ(i) wi 2 ≥ γi ∗ n=i wn Ri,κ(n) wn + σi (5.2) Donde el escalar σi2 es la potencia del ruido recibida en el usuario i y γi es el SINR deseado para dicho usuario. 5.1.1. Conformación óptima conjunta del lóbulo y Control de potencia La conformación óptima del lóbulo consiste en el diseño del conjunto de conformadores wi , dados los estimados de todas las matrices de correlación 5.1 Conformación óptima del lóbulo 24 del canal Ri,κ y niveles de ruido σi2 . La meta es minimizar la potencia total transmitida mientras se provee la suficiente SINR a cada terminal. El problema bien puede ser formulado como mı́n d wn∗ wn n=1 sujeto a wi∗ Ri,κ(i) wi∗ ≥ γi wn∗ Ri,κ(n) wn + γi σi2 (5.3) n=i Una serie de observaciones importantes en torno a este problema de optimización fueron hechas en [31], y son: 1. La función costo en (5.3) es continua y coercitiva, su valor converge a +∞ a lo largo de cualquier secuencia de sus argumentos tal que la norma de esos argumentos converja a +∞. Debido a que el conjunto de restricciones no es vacı́o y existe una solución viable, entonces, por el Teorema de Weierstrass existe un mı́nimo global. 2. Para el wi óptimo, todas las restricciones se cumplen con igualdad. Esto puede ser demostrado por contradicción: si existe un mı́nimo global con restricción de desigualdad estricta i en (5.3), entonces wi 2 puede ser disminuido sin violar las restricciones. Ası́, podemos obtener un punto viable con un valor de función costo menor que el mı́nimo global, lo cual es una contradicción. 3. Si las restricciones en (5.3) son normalizadas respecto al nivel de ruido, se obtiene un problema de optimización equivalente. Hay dos tipos de algoritmos que resuelven a (5.3) y ellos son los basados en la dualidad entre uplink y downlink y las soluciones de programación semidefinida. 5.1.2. Algoritmos basados en la dualidad La dualidad entre los canales uplink y downlink fue establecida por primera vez en [6]. Es posible construir una red virtual de uplink cuyas respuestas de los canales sean similares a aquellas del downlink. Después que los vectores conformadores receptores en las estaciones base del uplink virtual son encontrados, los mismos vectores son usados en cada iteración para el downlink. La matriz de ganancia del uplink converge a una matriz fija cuyos autovalores están dentro del cı́rculo unitario. A partir del hecho que los autovalores de la matriz de ganancias en el downlink y el uplink son los mismos, la iteración del downlink es convergente si la del uplink virtual también lo es. En consecuencia, bajo la condición de igualdad en el nivel de ruido en todos los receptores, tanto el uplink como el downlink tienen la misma región SINR alcanzable. Sin embargo, en el caso de diferentes niveles de ruido en los receptores, el problema sigue siendo 5.1 Conformación óptima del lóbulo 25 óptimo si las matrices de covarianza del canal son escaladas por las varianzas del ruido correspondientes. Una estrategia iterativa y razonable para minimizar el gasto en potencia transmitida fue derivada en [12]. También, una aproximación similar con control de congestión fue propuesta en [7]. 5.1.3. Programación Semi-Definida y Optimización Convexa En [9] el mismo problema de optimización fue considerado, presentando una solución alternativa usando optimización convexa. Un problema de optimización convexa consiste en la minimización de una función convexa sobre un conjunto convexo. El mı́nimo local de una función convexa es también el mı́nimo global, lo cual significa que no existen otros mı́nimos locales a los cuales la minimización pueda ser forzada. Durante la última década, las técnicas de optimización convexa, especf́icamente las de programación semi-definida y programación del cono de segundo orden, se han convertido en unas de las innovaciones más significativas realizadas en el área de la optimización matemática, encontrando aplicaciones en múltiples disciplinas como teorı́a de control y procesamiento de señales. El problema básico de conformación del lóbulo (5.3) es un problema cuadrático de optimización con restricciones cuadráticas no convexas, el cual en general es un problema NP-completo que no puede ser resuelto en tiempo razonable. De cualquier manera, para el caso especial de los canales de rango unitario, donde Ri,κ = hi,κ hi,κ ∗, (5.3) puede ser escrita como sigue: mı́n d wn∗ wn n=1 sujeto a |wi∗ hi,κ(i) |2 ≥ γi wn∗ Ri,κ(n) wn + γi σi2 n=i Im wi∗ hi,κ(i) = 0 (5.4) wi∗ hi,κ(i) ≥ 0 i = 1, . . . , d Lo cual pasa a ser un problema convexo porque las restricciones para cada i son solamente una transformación afı́n del cono convexo de segundo orden (x, y)x ∈ R, y ∈ CN , x ≥ y Además, el problema puede ser resuelto usando las técnicas de optimización 5.2 Algoritmos Descentralizados 26 convexas. Un enfoque de rango relajado es mostrado en [9], el cual provee mayor flexibilidad. Vale la pena notar que a través de este método, llamado relajación Lagrangiana, a veces no podemos obtener wi de rango uno, sino soluciones de alto rango que pueden ser tomadas como matrices de correlación para los conformadores. 5.2. Algoritmos Descentralizados Los algoritmos óptimos explicados en la sección anterior requieren completa CSI dentro y fuera de la celda. Un algoritmo descentralizado toma el problema original de optimización en (5.3) y lo soluciona para cada celda por separado. Como es obvio, el control conjunto de portencia y conformación del lóbulo no es posible en este enfoque, ası́ que es una solución subóptima, a pesar de que aún ası́ puede proporcionar buen rendimiento. Las restricciones especificadas en (5.2) son de la forma S ≥ γi Iintra + Iinter + N (5.5) Donde S denota la potencia de la señal deseada, Iintra y Iinter representan la interferencia en la misma celda y entre celdas distintas, respectivamente, y N es la potencia del ruido. Cuando la disposición de los canales en las estaciones base es hecha sin coordinación global, aun cuando podemos seguir estimando la interferencia en la misma celda, la interferencia entre celdas distintas ya no puede ser calculada de manera exacta. En consecuencia, necesitamos reconsiderar la suposición anterior de que la interferencia total puede ser exactamente calculada en un suscriptor dado. En las secciones que siguen, formularemos diferentes estrategias ad-hoc usadas para manejar la interferencia entre celdas distintas. 5.2.1. Margen SINR Incrementado Considere una estación base κ la cual tiene CSI de todos los móviles adentro de su propia celda, pero ninguna información disponible acerca de los canales en las celdas exteriores. La estrategia más simple consiste en ignorar el término de interferencia entre celdas distintas e incrementar el margen SINR por un factor β > 1, y establecer algunas nuevas restricciones. S ≥ βγi Iintra + N (5.6) Estas restricciones cambian el problema de optimización, ası́ que (5.5) seguirá cumpliéndose mientras (5.6) se sostenga para un β que satisfaga la condición β≥ 1 1 − γi Iinter S (5.7) 5.2 Algoritmos Descentralizados 27 Bajo el supuesto que β ≥ 1, la siguiente condición también debe ser verdadera Iinter 1 ≤ S γi (5.8) Por lo tanto, una manera de determinar β consiste en recolectar estadı́sticas del cociente Iinter /S y escoger un β tal que (5.7) se cumpla bajo un cierto lı́mite superior. Estadı́siticas de Iinter /S pueden ser enviadas a la estación base bien desde el administrador central de recursos o si no desde el propio móvil, dado que este último tenga una cierta capacidad de procesamiento se señales, muy básica. De cualquier manera, la cantidad de información enviada es reducida a sólo un escalar por móvil, convirtiéndose en un modelo de retroalimentación bastante reducida. El algoritmo trabaja con solamente el valor 90 percentil de Iinter /S promediado sobre un periodo de tiempo lo suficientemente largo, con lo cual la tasa de retroalimentación es muy baja. De cualquier modo, la ventana de tiempo en la cual tomamos el promedio debe ser inferior al tiempo de coherencia del canal. Ya que Iinter /S varı́a cuando cambiamos β, unas pocas iteraciones pueden necesitarse. Entonces, es importante probar convergencia. Una secuencia de trabajo para las iteraciones es detallada en la tabla 5.1. 1. β = 1 2. repetir 3. resolver (5.6) 4. enviar Iinter (90 % valor promedio) S → estación base 5. β antiguo = β 6. de (5.7) → β̂ 7. nuevo β = β̂ 8. hasta β antiguo == β̂ Cuadro 5.1: Solución algorı́tmica de SINR Incrementado 5.2.2. Término de Penalización Cuando incrementamos las restricciones de SINR, el lóbulo principal del patrón de radiación es incrementado en potencia, como también lo son los lóbulos laterales. Lóbulos laterales más altos significa más alta interferencia transmitida a otros usuarios, tanto adentro como fuera de la celda. Ası́ mismo, es una pérdida de energı́a. La idea aquı́ es añadir un término de penalización en 5.2 Algoritmos Descentralizados 28 el denominador de las restricciones de SINR para reducir el riesgo de lóbulos laterales más altos en los conformadores mı́n d wn∗ wn n=1 sujeto a |wi hi,κ |2 ≥ βγi , 2 2 2 n∈I(κ) |wn hi,κ | + σi + αwi ∀i ∈ I(k) (5.9) n=i Lo cual se reduce a (5.6) cuando α = 0. Puede argumentarse que la función costo trata por sı́ sola trata en la medida de lo posible de mantener pequeños todos los wi 2 y es claro que aumentar α incrementará la potencia transmitida total, ya que estaremos haciendo las restricciones más estrictas pero la potencia estará concentrada en el lóbulo principal. De todas formas, puede ser posible usar un valor inferior de β, para que el desempeño del sistema pueda resultar beneficiado. Una solución algorı́tmica es mostrada en la tabla 5.2. 1. β = 1, α > 0 2. repetir 3. resolver (5.9) 4. enviar Iinter (90 % valor promedio) S → estación base 5. β antiguo = β 6. de (5.7) → β̂ 7. nuevo β = β̂ 8. hasta β antiguo == β̂ Cuadro 5.2: Solución algorı́tmica por término de penalización 5.2.3. Restricciones adicionales Asumiendo que los móviles solamente tienen una antena omni-direccional, la suma de toda la energı́a recibida por la estación base κ en el uplink es y(t) = d qn hn,κ sn (t) + n(t) (5.10) n=1 Donde qn hn,κ sn es la señal uplink enviada desde el móvil n a la estación base κ. El usuario n puede estar tanto dentro como fuera de la celda. Esta expresión 5.2 Algoritmos Descentralizados 29 contiene la CSI entre la estación base κ y todos los móviles. Puesto que los canales más fuertes pueden ser reconocidos en la estación base, canales lejanos serán negligibles respecto a los más cercanos. Una vez que la destinación de los canales es hecha, la estación base puede determinar el estimado del vector de los canales, visto sólo como un vector complejo, de la señal de interés (SOI - Signal Of Interest), y obtener el valor de la señal. Ası́ mismo, el resto de los canales asignados a la estación base pueden ser discernidos de entre toda la información recibida. Si sustraemos el estimado de la SOI de (5.10) tenemos ỹ(t) = y(t) − h̃i,κ(i) s̃i (t) (5.11) Dada la reciprocidad del canal entre la data del uplink y el downlink, podemos manipular (5.11) para obtener estadı́sticas en torno al estimado de los canales interferidos a lo largo de un cierto perı́odo, lo cual puede ser expresado como N 1 Q̂i = ỹ(t)ỹ(t)∗ ≈ qn E hn,κ(i) h∗n,κ(i) + σn2 I N t=1 (5.12) n=i En los ejemplos numéricos, el momento estadı́stico E[hn,κ(i) h∗n,κ(i) ] puede ser tomado de la expresión formulada en (4.10), y entonces (5.12) se convierte en Q̂i = qn Ra ,n + σn2 I (5.13) n=i Donde Qi son matrices positivas y semidefinidas. Cuando normalizamos con respecto al canal entre la estación base y los móviles, los valores escalares qn pueden ser expresados como qn ∝ 1 hn,κ(i) 2 (5.14) El estimado de Qi , basado en las medidas uplink, puede ser usado para suprimir activamente la interferencia a los móviles pertenecientes a otras celdas que poseen un canal fuerte a la estación base. Esta supresión puede ser hecha bajo la forma de restricciones al problema de optimización del downlink como mı́n d wn∗ wn n=1 sujeto a |wi hi,κ |2 2 ≥ βγi , 2 n∈I(κ) |wn hi,κ | + σi ∀i ∈ I(k) n=i wi∗ Qi wi ≤ μi , ∀i ∈ I(k) (5.15) 5.2 Algoritmos Descentralizados 30 En consecuencia, esta estrategia trata de predecir la interferencia causada en usuarios particulares en las celdas cercanas que sufrirán en mayor parte por nuestra señal transmitida. Los factores escalares μi son constantes positivas usadas como una restricción para la interferencia producida por la estación base hacia el usuario especı́fico que hayamos escuchado más claro durante el uplink. Un μi muy grande significarı́a una libertad plena al conformador y por ende ninguna restricción, mientras que un μi muy pequeño podrı́a causar un escenario no viable. Un esquema para esta solución puede ser visto en la tabla 5.3 1. β = 1, μi > 0 2. repetir 3. resolver (5.15) 4. enviar Iinter (90 % valor promedio) S → estación base 5. β antiguo = β 6. de (5.7) → β̂ 7. nuevo β = β̂ 8. hasta β antiguo == β̂ Cuadro 5.3: Solución algorı́tmica con restricciones adicionales Capı́tulo 6 Simulaciones y Análisis de Resultados Los algoritmos descentralizados fueron probados en un ambiente de simulación. En este capı́tulo discutiremos en profundidad las condiciones bajo las cuales se ejecutó la simulación y los resultados que fueron obtenidos. A partir de ellos, probamos la convergencia de las soluciones, estudiamos algunas de las caracterı́sticas del manejo de la interferencia en cada algoritmo, comparamos los patrones de radiación obtenidos y mostramos el desempeño global en los escenarios simulados. Las simulaciones fueron hechas para mostrar el comportamiento de los algoritmos propuestos. No tienen como objetivo la evaluación del desempeño en un sistema completo. Para efectuar esto, se necesitarı́an supuestos más ambiciosos en esquema de acceso múltiple, modulación y codificación. La interacción entre procesamiento espacial y procesamiento en tiempo y frecuencia está más allá del alcance de este proyecto. 6.1. Ambiente de Simulación El sistema multicelular es simulado con arreglos circular uniforme en todos los puntos de acceso, distribuidos en un área dividida en hexágonos regulares como en la figura 6.1. Para ignorar efectos de borde, el modelo contiene 19 celdas y el análisis sólo se realiza en las siete celdas más internas sin perder generalidad. Estaciones móviles se encuentran dispersas en una distribución uniforme. La carga de usuarios por celda es variada en las simulaciones. Los móviles son asignados al canal más fuerte que tengan con las estaciones base. Expresamos los vectores de canal de comunicación como una función del ángulo entre el móvil y la estación base y la desviación estándar de la dispersión angular. Todos los supuestos referentes a propagación multitrayectos y canales con desvanecimiento Rayleigh plano en frecuencias detallados anteriormente en este reporte se sostienen para las simulaciones. Suponemos que el desvanecimiento rápido se encuentra distribuido normalmente. La ganancia del canal es 6.2 Resultados 32 afectada por la pérdida del trayecto dependiente de la distancia con exponente de pérdidas αatt y el desvanecimiento lento distribuido de manera log-normal. Número de escenarios Número de celdas simuladas Número de celdas evaluadas Factor de reúso Máxima carga por celda (de usuarios) Nivel de ruido SINR Número de elementos de antena Radio del arreglo circular uniforme Número de trayectos de propagación Desviación estándar del desvanecimiento lento Coeficiente de pérdidas por trayecto Varianza de la dispersión angular 300 19 7 1 3 0 dB 10 dB 8 λ 3 30 8 dB 3,5 3 grados Cuadro 6.1: Parámetros de Simulación La solución óptima es generada de acuerdo a (5.4), la cual genera tanto la expresión de potencia como el filtrado especial de manera conjunta. Los diferentes algoritmos descentralizados son ejecutados siguiendo las instrucciones especificadas en el capı́tulo previo. Para el cálculo de optimización convexa, usamos el paquete libre cvx, desarrollado por Michael Grant, Stephen Boyd, y Yinyu Ye en la Universidad de Stanford. Este software convierte a Matlab en un lenguaje modelador, permitiendo la especificación de restricciones y objetivos usando sintaxis estándar de Matlab. Un sumario de los parámetros de simulación usados pueden ser vistos en la tabla 6.1. 6.2. Resultados Las figuras 6.2, 6.3 y 6.4 muestran la convergencia del parámetro β en los diferentes algoritmos descentralizados propuestos en este proyecto. Para la solución de SINR Incrementado, podemos ver que la convergencia es diferente a la que habı́amos esperado. β parece decrecer cuando el número de usuarios por celda es incrementado a 3, desafiando nuestro supuesto inicial. Al mirar la figura 6.5 podemos ver también que el cociente entre la interferencia entre celdas distintas y la señal es muy alto para este caso, ası́ que (5.8) no se sostiene para el sistema simulado cuando hay dos o más usuarios por celda. Ya que la estación base no conoce nada acerca del nivel de interferencia entre celdas distintas al momento que los conformadores son resueltos, el algoritmo trata un valor diferente de β que no es correcto. 6.2 Resultados 33 15 Base Station Mobile Station 10 5 0 −5 −10 −15 −15 −10 −5 0 5 10 15 Figura 6.1: Modelo del ambiente celular simulado: caso de 2 usuarios por celda Este problema se extiende hacia otros algoritmos, pues en todos ellos hemos trabajado de alguna manera u otra con el SINR incrementado. Podemos observar en la figura 6.6 que, para el algoritmo de Término de Penalización, (5.8) se cumple aproximadamente para uno o dos usuarios por celda, y la convergencia de β satisface nuestras expectaciones (que β aumenta a medida que aumentamos el número de interferentes). Esta lógica parece confirmarse cuando observamos la figura 6.7, donde (5.8) se cumple para todos los casos y β converge tal y como se esperaba. La razón es que el algoritmo de restricciones adicionales es el único algoritmo en el cual la estación base tiene cierto control sobre la interferencia hacia otras celdas y es capaz de mantenerla bajo un cierto valor. Luego, las figuras 6.8 y 6.9 reflejan cómo variamos los parámetros principales mientras se preservó fija la carga de la celda. En la figura 6.8, consideramos diferentes valores de α para ser incluidos en (5.9) como un control para niveles de lóbulos laterales. Evaluando el porcentaje de usuarios exitosos, eso es los móviles donde SINR≥ γi , observamos que el desempeño empeora a medida que incrementamos el nivel de α. Pero un valor muy pequeño de α resulta también en una mala decisión y pofrı́a afectar la manera en que los conformadores son calculados, puesto que la herramienta cvx es susceptible de errores al lidiar con cantidades cercanas a 1/4 y no puede alcanzar convergencia. En el caso del algoritmo de Restricciones Adicionales, la mejor selección para los escalares μi fue la de los valores medios (20 ≤ μi ≤ 50), tal y como fue 6.2 Resultados 34 probado en la figura 6.9. Pequeños μi significarı́an restricciones muy estrechas en la solución (5.15) que podrı́an conducir a la inviabilidad de la solución, mientras que un μi extremadamente grande brinda una completa libertad al algoritmo, causando que la interferencia no sea restringida para nada, terminando en un esquema igual al de (5.6). Un ejemplo de los patrones de radiación resueltos por los algoritmos pueden ser vistos en las figuras 6.10, 6.11 y 6.12. Es claro que la solución óptima coloca ceros en la dirección de los interferentes y coloca el lóbulo principal en el ángulo óptimo donde menos usuarios son afectados. Los algoritmos descentralizados acoplan los conformadores con el canal del usuario de interés, para que el lóbulo principal apunte directamente al ángulo θ donde el usuario esté localizado. En el caso especı́fico dibujado en las figuras mencionadas, el móvil de interés i se encuentra en θi ≈ −50◦ y existe un interferente j dentro de la misma celda a θj ≈ 40◦ . Como podemos observar, todos los algoritmos se aproximan a la solución forzante a cero para el móvil j, colocando un cero en esa dirección. Pero el algoritmo óptimo es el único que, aprovechando la información global de los canales, puede colocar m − 1 ceros en las direcciones interferentes. Para las estrategias de SINR incrementado y Término de Penalización, los ceros pueden ser ubicados sólo en dirección de los interferentes situados en la misma celda. En la figura 6.13, es mostrado cómo la potencia es controlada por los algoritmos descentralizados, especialmente para el caso de las Restricciones Adicionales. Sin embargo, la optimización de la potencia falla cuando analizamos la probabilidad de caı́da de servicio, la cual es dibujada en 6.14. Que la conformación óptima del lóbulo arroje una probabilidad de caı́da de servicio igual a cero sólo es posible en la simulación donde la solución al problema convexo expresado en (5.4) es siempre posible de calcular. Ya que la capacidad de cálculo fue llevada al máximo durante las simulaciones, un esquema óptimo como éste no serı́a práctico en sistemas de operación real. Pero asumiendo casi infinita capacidad de cómputo, la fortaleza del algoritmo de optimización convexa sigue siendo notable. La probabilidad de caı́da de servicio en los algoritmos descentralizados fue en cierto modo más pobre de lo que se esperaba. Ya que aplicamos el SINR Incrementado en todas las técnicas, una escogencia de β que cumpliera la condición (5.7) para 90 % de los casos, se supuso que arrojarı́a una equivalente caı́da de servicio alrededor de 0,1 mientras todos los supuestos previos fueran satisfechos. Un valor cercano al 0,1 fue obtenido para el caso de un usuario por celda, pero el desempeño disminuye dramáticamente a medida que incrementamos el número de los usuarios. La razón por la cual la estrategia de SINR Incrementado pareciera que resulta mejor que otros algoritmos es solamente porque este algoritmo encuentra mayor cantidad de soluciones viables que los otros, más restrictivos. Cuando las restricciones de interferencia hacia otras celdas no pueden ser cumplidas por los algoritmos de Término de Penalización y Restricciones Adicionales, el escenario es tratado como un único problema no realizable y ningún móvil es servido. Puesto que el problema es solucionado en cada estación base, una restricción inviable significa una celda no resuelta. 6.2 Resultados 35 2.4 1 user/cell 2 users/cell 3 users/cell 2.2 2 β 1.8 1.6 1.4 1.2 1 0 2 4 6 8 Number of iterations 10 Figura 6.2: Convergencia de β para el Algoritmo de SINR Incrementado 1.4 1 user/cell 2 users/cell 3 users/cell β 1.3 1.2 1.1 1 0 2 4 6 8 Number of iterations 10 Figura 6.3: Convergencia de β para el Algoritmo de Término de Penalización 6.2 Resultados 36 3 1 user/cell 2 users/cell 3 users/cell β 2.5 2 1.5 1 0 2 4 6 8 Number of iterations 10 Figura 6.4: Convergencia de β para el Algoritmo de Restricciones Adicionales −2 1 user/cell 2 users/cell 3 users/cell −4 Iinter/Signal dB −6 −8 −10 −12 −14 −16 −18 0 2 4 6 8 Number of iterations 10 Figura 6.5: Convergencia de Iinter /S para el Algoritmo de SINR Incrementado 6.2 Resultados 37 −6 1 user/cell 2 users/cell 3 users/cell Iinter/Signal dB −8 −10 −12 −14 −16 −18 −20 0 2 4 6 8 Number of iterations 10 Figura 6.6: Convergencia de Iinter /S para el Algoritmo de Término de Penalización −9 1 user/cell 2 users/cell 3 users/cell −10 Iinter/Signal dB −11 −12 −13 −14 −15 −16 −17 0 2 4 6 8 Number of iterations 10 Figura 6.7: Convergencia de Iinter /S para el Algoritmo de Restricciones Adicionales 6.2 Resultados 38 40 % Succesful Users 35 30 25 20 15 10 5 −3 −2 −1 0 log10(α) Figura 6.8: Desempeño del Algoritmo de Término de Penalización cuando el parámetro α es variado % Succesful Users 44 42 40 38 36 34 0.5 1 1.5 2 log10(μi) 2.5 3 Figura 6.9: Desempeño del Algoritmo de Restricciones Adicionales cuando el parámetro μi es variado 6.2 Resultados 39 40 θ Optimal BF Increased SINR Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 50 Degrees 100 150 Figura 6.10: Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de SINR Incrementado, comparado a la Conformación Óptima 40 θ Optimal BF Penalty Term Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 Degrees 50 100 150 Figura 6.11: Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de Término de Penalización, comparado a la Conformación Óptima 6.2 Resultados 40 40 θ Optimal BF Additional Constraints Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 50 Degrees 100 150 Figura 6.12: Patrón de radiación dibujado para un móvil resuelto por el Algoritmo de Restricciones Adicionales, comparado a la Conformación Óptima Optimal BF Increased SINR Penalty Term Additional Constraints 80 Power in dB 60 40 20 0 1 2 Number of Users 3 Figura 6.13: Potencia Transmitida Total para cada algoritmo de acuerdo al número de usuarios por celda 6.2 Resultados 41 Optimal BF Increased SINR Penalty Term Additional Constraints 1 Outage Probability 0.8 0.6 0.4 0.2 0 1 1.5 2 2.5 Number of Users 3 Figura 6.14: Probabilidad de Caı́da de Servicio de cada algoritmo de acuerdo al número de usuarios por celda Capı́tulo 7 Conclusiones Las restricciones y modificaciones hechas al problema original de conformación del lóbulo para el downlink pudieron ser ensambladas como problemas de optimización convexa y probaron alcanzar convergencia. Siguiendo una serie de algoritmos descentralizados que no requieren información global de los canales, las estaciones base pueden encontrar un conjunto de vectores peso que colocan ceros hacia los interferentes locales ası́ como también para tratar de controlar el nivel de interferencia hacia otras celdas. La convergencia de parámetros especı́ficos como β, α y μ dentro de cada algoritmo, sugiere la idea de que cada red celular puede ser caracterizada con su propio valor ad-hoc. Además, podemos generalizar la solución y una red con determinadas caracterı́sticas puede usar un conjunto de parámetros predeterminados obtenidos por simulación previa. Sin embargo, todos los algoritmos requieren la existencia de una solución viable. Cuando la carga de la celda es aumentada y demasiados móviles terminales quieren comunicarse al mismo tiempo usando el mismo canal, existe un riesgo que la solución al problema de optimización para usuarios locales no exista. En estos escenarios, el problema de optimización debe ser reducido: acceso al sistem deberı́a ser negado a algunos móviles para mejorar el desempeño. También, un posible trabajo futuro consiste en resolver el problema de control de admisión, eso es cómo admitir o remover móviles en el sistema. Sin la implementación del control de congestión, es difı́cil decir si las técnicas propuestas pueden ser usadas en el campo real. Podemos ver que añadiendo restricciones a los algoritmos descentralizados no ofrece ninguna ventaja, ya que estas restricciones no operan activamente en los conformadores. Lo cual resulta en que podemos encontrar un conjunto válido de conformadores que cumplan dichas restricciones y sin embargo el problema de SINR sigue siendo sub-óptimo. Una reformulación del problema pudiera necesitarse. Finalmente, recordamos que estas técnicas son solo parte de un problema mayor, el cual incluye todos los servicios de la red de comunicación móvil. Los algoritmos propuestos, basados en una estrategia de SDMA (Space Division Multiple Access - Acceso Múltiple por División Espacial), no son la única y última manera de garantizar servicio en los usuarios. Como fue explicado a lo 43 largo del proyecto, existen muchas alternativas. Como técnica SDMA, pudiera ser interesante estudiar en qué manera la separación angular entre los usuarios puede afectar el desempeño de estos algoritmos, un factor que no fue contabilizado en este proyecto (puesto que trabajamos con escenarios de localización aleatoria) Es el trabajo de investigadores e innovadores en el área desarrollar y probar nuevas tecnologı́as que puedan superar estas dificultades y proporcionar un mejor servicio en las redes de comunicación móvil. Bibliografı́a [1] T. S. Rappaport. Wireless Communications. Principles and Practice Second Edition. Prentice Hall. 2002. [2] L. C. Godara. Applications of antenna arrays to mobile communications. I. Performance improvement, feasibility and system considerations. Proceedings of the IEEE. Vol. 85, No. 7, July 1997. [3] ——. Application of Antenna Arrays to Mobile Communications, Part II: Beam-Forming and Direction-of-Arrival Considerations. Proceedings of the IEEE. Vol. 85, No. 8, August 1997 7, July 1997. [4] ——. Smart Antennas. CRC Press. 2004 [5] C. Farsakh and J. A. Nossek. Channel allocation and downlink beamforming in an SDMA mobile radio system. 6th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 1995. Vol. 2, September 1995. [6] F. Rashid-Farrokhi, K. J. R. Liu and L. Tassiulas. Transmit beamforming and power control for cellular wireless systems. IEEE Journal on Selected Areas in Communications. Vol. 16, Issue 8, October 1998. [7] R. Stridh, M. Bengtsson and B. Ottersten. System Evaluation of Optimal Downlink Beamforming with Congestion Control in Wireless Communication. IEEE Transactions on Wireless Communications Vol. 5, No. 4, April 2006. [8] M. Bengtsson and B. Ottersten. Optimal and suboptimal transmit beamforming, Chapter 18 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001. [9] ——. Optimal downlink beamforming using semidefinite optimization. Proceedings of 37th Annual Allerton Conference on Communication, Control and Computing. September 1999. [10] M. Schubert and H. Boche. Solvability of coupled downlink beamforming problems. Proceedings of IEEE Global Telecommunications Conference 2001. Vol. 1, November 2001. BIBLIOGRAFÍA 45 [11] ——. A unifying theory for uplink and downlink multiuser beamforming. Proceedings of 2002 International Zurich Seminar on Broadband Communications. February 2002. [12] ——. Solution of the multiuser downlink beamforming problem with individual SINR constraints. IEEE Transactions on Vehicular Technology Vol. 53, No 1, January 2004. [13] N. Wang, P. Agathoklis and A. Antoniou. A subspace multiuser beamforming algorithm for the downlink in mobile communications. IEEE Transactions on Circuits and Systems –II: Express Briefs. Vol. 53, No. 8, August 2006. [14] T. Asté, P. Forster, L. Féty, and S. Mayrargue. Downlink beamforming avoiding DOA estimation for cellular mobile communication. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing. Vol. 6, May 1998. [15] M. Grant, S. Boyd and Y. Ye. cvx User’s guide. January 14, 2007. http://www.stanford.edu/∼boyd/cvx/cvx usrguide.pdf [16] S. Boyd and L. Vandenberghe. Convex Optimization Cambridge University Press. 2004. [17] J. F. Sturm. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Department of Quantitative Economics, Maastricht University, The Netherlands, 1999. http://sedumi.mcmaster.ca [18] R. Mailloux. Phased Array Antenna Handbook Second Edition. Artech House. 2005. [19] Y. Yang, Chao Sun and C. Wan. Theoretical and experimental studies on broadband constant beamwidth beamforming for circular arrays. In Proceedings OCEANS 2003. Volume 3. 22-26 September 2003. [20] Barry D. Van Veen and Kevin M. Buckley. Beamforming - a versatile approach to spatial filtering. IEEE Acoustics, Speech, and Signal Processing Magazine. Vol. 5, No. 4 April 1988. [21] D. G. Brennan. Linear Diversity Combining Techniques. Proceedings of the IEEE Vol. 91, No. 2, February 2003 [22] S. Drabowitch, A. Papiernik, H. D. Griffiths, J. Encinas and B. L. Smith. Modern Antennas 2nd edition. Springer 2005. [23] R. A. Monzingo and T. W. Miller. Introduction to Adaptive Arrays. John Wiley & Sons. 1980 [24] A. R. Modarressi and R. A. Skoog. An Overview of Signal System No. 7. Proceedings of the IEEE. Volume 80, No. 4, April 1992. BIBLIOGRAFÍA 46 [25] W. C. Y. Lee. Mobile Communications Design Fundamentals. Second Edition. John Wiley & Sons, Inc. 1993. [26] S. S. Rappaport. Blocking, hand-off and traffic performance for cellular communication systems with mixed platforms. In IEE Proceedings I Communications, Speech and Vision Volume 140, Issue 5, October 1993 [27] M. Rajaratnam. Takawira, F. Hand-off traffic modelling in cellular networks IEEE Global Telecommunications Conference, 1997. GLOBECOM ’97. Volume 1, 3-8 November 1997 [28] B. Sklar. Fading Channels, Chapter 4 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001. [29] E. Björson. Beamforming utilizing channel norm feedback in multiuser MIMO systems Master Thesis, Lund University in cooperation with KTH Royal Institute of Technology, 2007. [30] H. Krim and M. Viberg. Two decades of Array Signal Processing Research: the parametric approach. IEEE Signal Processing Magazine. Vol. 13, No. 4, July 1996 [31] E. Visotsky and U. Madhow. Optimum beamforming using transmit antenna arrays. Proceedings VTC’ 99, IEEE, Houston, TX. Vol 1. May 1999. [32] A. Narula, et. al. Efficient use of side information in multiple-antenna data transmission over fading channels. IEEE Journal on Selected Areas in Communications Volume 16, Issue 8, Oct. 1998 [33] D.J. Love, R.W. Heath Jr., et. al. What is the value of limited feedback for MIMO channels? IEEE Communications Magazine Volume 42, Issue 10, Oct. 2004 [34] Boon Poh Ng and Meng Hwa Er. Basic Array Theory and Pattern Synthesis Techniques, Chapter 16 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001. Downlink beamforming with reduced feedback GABRIEL CASTELLANOS Master’s Degree Project Stockholm, Sweden XR-EE-SB 2007:007 Abstract Different schemes for optimal downlink beamforming in a multiuser multicell cellular system, have been proposed in the literature, based on global knowledge of the channels between all base stations and all mobile stations. However, in practice, a very large overhead would be required to obtain and communicate this channel knowledge. On the other hand, precise channel knowledge at a certain base station should only be needed for users that are strongly influenced by that specific base station. The purpose of this project is to implement and evaluate schemes that solve the downlink beamforming problem for each cell separately or for small groups of cells at a time, using approximations to handle the intercell interference. Acknowledgments I would like to express my thankfulness to my supervisor Mats Bengtsson for suggesting the research topic and for all valuable help, advice and discussions. Also, to the International Office at the Royal Institute of Technology, specially Cecilia Forsmann, and the International Relations Department at Universidad Simón Bolı́var for their support and giving me the opportunity to conduct my thesis project in Stockholm. Finally, I would like to thank my friends and family for their encouraging words along these months of hard work. Contents 1. Introduction 1.1. Problem Statement . . . . . . . 1.2. Methodology . . . . . . . . . . 1.2.1. General Model . . . . . 1.2.2. Algorithm . . . . . . . . 1.2.3. Simulation Environment 1.3. Outline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 2 3 3 3 4 4 2. Mobile Radio Environment 2.1. Cellular Environment . . . . . . . . . . . . . . . . . . . . . 2.1.1. Base Stations . . . . . . . . . . . . . . . . . . . . . . 2.1.2. Mobile Stations . . . . . . . . . . . . . . . . . . . . . 2.1.3. Frequency Reuse . . . . . . . . . . . . . . . . . . . . 2.1.4. Cell Splitting . . . . . . . . . . . . . . . . . . . . . . 2.1.5. Hand-Off . . . . . . . . . . . . . . . . . . . . . . . . 2.2. Noise and Interference . . . . . . . . . . . . . . . . . . . . . 2.2.1. Noise-Limited and Interference-Limited Environment 2.2.2. Intracell and Intercell Interference . . . . . . . . . . 2.2.3. Signal to Interference Plus Noise Ratio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 7 7 8 8 9 9 9 10 10 10 3. Antenna Array Transmitter 3.1. Antenna Array Model . . . . . 3.2. Beamforming . . . . . . . . . . 3.2.1. Uplink Beamforming . . 3.2.2. Downlink Beamforming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 12 13 14 14 4. Channel Modeling 4.1. Multipath propagation . . . . . . . . 4.2. Fading . . . . . . . . . . . . . . . . . 4.2.1. Large Scale Fading . . . . . . 4.2.2. Small Scale Fading . . . . . . 4.3. Narrowband channel model . . . . . 4.4. Multiple users and multiple antennas 4.5. Downlink Channel Estimation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 16 17 18 18 18 19 20 . . . . . . . . 4.6. Feedback . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5. Downlink Beamforming Algorithms 5.1. Optimal Beamforming . . . . . . . . . . . . . . . . . . . . . . 5.1.1. Joint Optimal Beamforming and Power Control . . . . 5.1.2. Duality-Based Algorithms . . . . . . . . . . . . . . . . 5.1.3. Semi-Definite Programming and Convex Optimization 5.2. Decentralized Algorithms . . . . . . . . . . . . . . . . . . . . 5.2.1. Increased SINR Margin . . . . . . . . . . . . . . . . . 5.2.2. Penalty Term . . . . . . . . . . . . . . . . . . . . . . . 5.2.3. Additional Constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 23 24 24 25 26 27 27 28 29 6. Simulations and Performance Study 32 6.1. Simulation Environment . . . . . . . . . . . . . . . . . . . . . . . 32 6.2. Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 7. Conclusions 43 Chapter 1 Introduction The exceptional growth of mobile communication and wireless networks compels today 3G systems to adapt themselves to rising number of mobile subscribers, wireless network access, mobile services and applications. The forthcoming 4G (fourth generation) mobile communication systems are expected to solve still-remaining unanswered problems of 3G systems and to provide a wide variety of new services, from high-quality voice to high-definition video to high-data rate wireless channels. In these future wireless systems traffic will be asymmetric: more information is transmitted from the access point to the terminal than in the opposite way. This implicates that the downlink is the most critical part of the communication and where most work has to be done in order to increase system capacity. Nowadays, mobile communication service providers pursue to include more cellular telephone conversations into the same amount of bandwidth and to grant a better service to their customers without changing the entire wireless network platform. This can be achieved by improving the performance of downlink data detection. There are many parameters that can measure such performance, being the Signal to Interference Plus Noise Ratio (SINR) the most important one. In any system, there is a minimum SINR that has to be maintained for each user in order to keep the expected bit error rate below a given limit. Thus, handling interference becomes a critical part of system optimization. One suitable and relatively cheap approach to solve this situation is using a receiver and transmitter strategy based on antenna arrays which has the capability to cancel Co-Channel Interference (CCI) [2]. The beam pattern of the array is adjusted to suit the requirements by combining signals from different antennas with appropriate weighting in a process called beamforming. The downlink beam can be pointed electronically from the base station in direction to the target mobile station and reduce interference on the downlink signals to other mobiles. Downlink differs from uplink beamforming because the choice for the weight vectors not only affects the link between the access point and the target user, but also mobiles either within the same cell or outside the cell. Also, if the 1.1 Problem Statement 2 power emitted at the base station is unnecessarily increased to force the intracell interference down to zero, the interference emitted into neighboring cells will be increased too. Hence, the design of downlink beamformers from the antenna arrays in the base stations to the mobiles must achieve a trade-off situation where the transmission power is minimized while maintaining the quality of service requirements. Different solutions have been presented (see [8] for an overview). Convex optimization methods applied to optimal beamforming have proven efficient solutions and guaranteed convergence speed. Furthermore, it is very easy to introduce modifications, for example adding extra constraints on the dynamic range or adding increased robustness to channel estimation errors. However, optimal solutions require full channel knowledge at each base station, which sometimes is difficult to obtain. An ideal option consists in the connection of all base stations to a central resource manager that receives all channel information available as a system feedback. In this scheme, we assume that all channel information is available to the central resource manager and it is an input to the optimal beamforming algorithm. Then, the beamforming algorithm attempts to maximize the SINR for every scheduled user. But such scheme creates a signalling overhead, which is required to collect all the channel information. Besides, the beamforming complexity and the number of operations are escalated, and more feedback delays between the stations and the central resource manager are generated. On the other hand, precise channel knowledge at a certain base station should only be needed for users that are strongly influenced by that specific base station. There is also an increasing interest on moving the intelligence in a wireless network towards the edge of the network (the base stations). 1.1. Problem Statement The purpose of this project is to develop new algorithms that solve the downlink beamforming problem individually for each cell. Channel information inside each cell is known, therefore intracell interference can be handled exactly. But channel information outside the cell is unknown, so it is necessary to create ad hoc strategies to handle the intercell interference. These strategies, which are analysed on Chapter 5, basically modify or/and add constraints to the downlink beamforming problem, using approximations to handle the intercell interference. We evaluate these methods against the optimal joint solution, which is considered as a benchmark. Through the measure of the outage probability for each algorithm, we are able to know how often the system can fulfill the SINR constraints, either globally or per user. Besides, because it is also wanted to minimize the power used at any base station to transmit the signal to its allocated mobile stations, the total transmitted power is considered too as a performance measure. The main goals of the project are: 1. To develop new decentralized downlink beamforming algorithms by adding 1.2 Methodology 3 and/or modifying the constraints of the original joint optimal problem, while using convex optimization as a method to achieve a global minimum solution 2. To design a simulation environment where valuable data results from the algorithms can be collected through averaging performance in several scenarios 3. To compare performance measures from the simulation data to the optimal solution benchmark and draw conclusions from this analysis Scheduling and wideband systems are outside the scope of this project. Congestion control schemes may be executed as a future work in this area. 1.2. Methodology 1.2.1. General Model The performance of the suggested downlink algorithms is illustrated in a simulated scenario shaped as a regular hexagonal cell-divided area. In order to ignore edge effects, the model contains enough cells so that the analysis can be made only in the most inner cells without losing generality. The base stations are located in the center of each cell and modeled according to an uniform circular array (UCA) specified on [14]. The mobile stations are spread over the cells in an uniform distribution. Base station assignment is trivial (a mobile location is allocated to the base station with the strongest channel). We consider multi-path propagation and frequency flat Rayleigh fading channels. Fast fading is supposed to be normally distributed while shadow fading has a log-normal distribution. This project does not study in depth how the interfering signals arrival angle is calculated, neither the interest mobile signal. Information about spatial location on the field is defined by the antenna array response, according to the characteristic equation of the model used to such purpose. This response is directly included in the channel vectors. Due to practical matters, the channel vectors between base stations and randomly dispersed mobile stations are generated during simulation. The system is assumed to be Time Division Duplex (TDD) with a short delay between uplink and downlink time slots compared to the coherence time of the channel. This allows us to use the uplink data for the downlink channel estimate. 1.2.2. Algorithm Different schemes are studied to solve the downlink beamforming optimization problem. With the convex optimization solution proposed in [9] it is very easy to introduce modifications. However, the number of variables used is higher than in other approaches. For cases where the uplink channel data can be used 1.3 Outline 4 as a good estimate of the instantaneous downlink channel, an efficient algorithm for optimum beamforming sketched in [9] and [8] can be used. This method allows to work out the set of constraints and to make them linear transformations of the second-order convex cone. By doing this, the problem has become a convex optimization problem with second-order constraints, which has several interior point methods available. We will take this techniques as a start point and from then develop our own adaptations according to the constraints we face in the modeling. 1.2.3. Simulation Environment To implement the optimization problem, the freely available package cvx1 will be used. This software turns Matlab into a modeling language, allowing constraints and objectives to be specified using standard Matlab expression syntax. Details about this software and convex optimization can be found in [15] and [16]. In the cvx version that is going to be used, SeDuMi is the only core solver supported. Further information on SeDuMi is given in [17]. 1.3. Outline Chapter 1 Introduction Gives an introduction to the work, specifying background, scope and an outline of the text body. 1.1 Problem Statement 1.2 Methodology General Model, Algorithms and Simulation Environment 1.3 Outline Chapter 2 Mobile Radio Environment details of the mobile communication model used in the project. 2.1 Cellular Environment Base Stations, Mobile Stations, Frequency Reuse, Cell Splitting and Hand-Off 2.2 Noise and Interference Noise-Limited and Interference LimitedEnvironment Chapter 3 Antenna Array Transmitter introduces the transmitter strategy based on antenna arrays. Thorough aspects include the antenna array response and the beamforming process. Also, the problem of transmitted power will be discussed as well as the signalling between antennas. 3.1 Antenna Array Model 3.2 Beamforming Uplink and Downlink Beamforming 1 Developed by Michael Grant, Stephen Boyd, and Yinyu Ye at Stanford University 1.3 Outline 5 Chapter 4 Channel Modeling in this chapter the analytic channel model used is explained. Channels between users and access points are supposed to be narrow band, multi-path and subject to Rayleigh fading. A distinction between global and local channel knowledge will be pointed, as some algorithms assume either of them. 4.1 Multi-path Propagation 4.2 Fading Shadow Fading and Fast Fading 4.3 Narrowband Channel Model 4.4 Multiple Users and Multiple Antennas 4.5 Downlink Channel Estimation 4.6 Feedback Chapter 5 Downlink Beamforming Algorithms contains the main choice for optimum beamforming, based on the fact that the system should provide an acceptable quality of service with the less cost, while serving as many users as possible. The specific optimal algorithm used as benchmark will be depicted. Statistical response to variations in interference and noise levels will be also displayed. 5.1 Optimal Beamforming Joint Optimal Beamforming and Power Control, Duality-Based Algorithms, Semi-Definite Programming and Convex Optimization 5.2 Decentralized Algorithms Increased SINR Margin, Penalty Term, Additional Constraints Chapter 6 Simulations and Performance Study statistic results of the algorithms performance compared to the optimal benchmark and to each other 6.1 Simulation Environment 6.2 Results Chapter 7 Conclusions Bibliography Chapter 2 Mobile Radio Environment In 1897 Guglielmo Marconi proved that the wireless telegraph system he had assembled was able to provide contact across the Bristol Channel in United Kingdom. The foundations of radio communications were born then and ever since new wireless methods and services have been adopted by customers around the world. As usual, the technology was first used in the battlefield, and the 20th century gave plenty of opportunities. The ability to provide wireless communication service to an entire population was introduced when Bell Laboratories developed the cellular concept in the 1960s and 1970s. The necessity was obvious: last century, the human specie became increasingly mobile. Crafts such as the internal combustion engine, automobile and plain were invented and cheap and apparently never scarce fossil fuel contributed to build a world that is not only on wheels, but on wings, over air, land and water. Digital and RF circuit fabrication improvements, new large-scale integration, and other miniaturization technologies made mobile radio equipment smaller, cheaper and more reliable. This allowed to people to carry their phones everywhere indoors or outdoors. The low cost infrastructure needed to support mobile users also encouraged companies to offer their services in this area. Far-off locations were easily connected with a network that is inexpensive when compared to the telephonic copper cable. It is expected that the market growth of mobile communication systems will continue at even greater pace during the next decade. Today, the mobile phone is more than just a phone. Next Generation Networks provide the opportunity to send messages, e-mails, navigate on the Web, listen to music, e-shopping, play videogames and much more. Some analysis even dare to forecast that the mobile phone will be the center of all our ordinary life activities, if it has not already become so. Voice and data converging systems define a challenge for today telecommunication engineers. 2.1 Cellular Environment 2.1. 7 Cellular Environment To provide service to the population of mobile users, several designs have been established, but the cellular model has proven to be one of the most successful. A cellular radio environment makes a finite spectrum or bandwidth to be available throughout a certain geographic area. This area served is divided in small areas known as cells. Two types of radio channels are used: control channels to carry control signals and traffic channels to carry messages. Control signals are used to set up calls and handle other control functions for idle units. The traffic channels are used to carry voice and data information. Depending on the direction of the signals, channels can also be classified in downlink or forward link (from the base station transmitter towards the mobile receiver) and uplink or reverse link (when the mobile phone is the transmitter and the base station comes to be the receiver). 2.1.1. Base Stations Each cell contains a base station, which is connected to a Mobile Switching Center (MSC), communicates to mobile phones on the site by radio links, and connects these mobiles to the Public Switching Telephone Network (PSTN). Radio links between mobile subscribers and base stations are established using a secure Common Air Interface (CAI), designed in order to maintain a handshake communication protocol. CAI provides reliability on the information sent between the mobile and base station, specifying speech and channel coding. The function of the base station is to act as the central point of network access for any subscriber within its own allocated cell. It is the basic building block in a cellular network. When many cellular telephone systems that provide coverage throughout a limited area are interconnected, the result makes an intercontinental wireless network which can cover the whole earth surface. Wireless networks are highly dynamic compared to the static PSTN, because the network configuration is rearranged everytime a subscriber moves from one cell to another. Many users can request service from any physical location, moving at any velocity, and the MSC must provide them with a portion of a limited spectrum. To interconnect most of the cellular MSCs, the SS7 signaling protocol [24] is widely used along the world. The complexity of the mobile communication network makes compulsory the use of techniques such as frequency reuse, cell splitting and spatial filtering. The base station consist typically of an antenna array of transmitters and receivers which simultaneously handle full duplex communications. An inside to the characteristics of this array will be given in chapter 3. The optimum antenna location for a base station inside a cell it is not easy to determine [25]. Irregular terrain configuration causes an irregular footprint at typical distances of 13 km from the base station. Also the location of one antenna affects the rest of the antennas because of interference. A typical criteria design consists on a low-area location but increasing the antenna height. The reception level at the 2.1 Cellular Environment 8 cell boundary must be decided on basis of the mobile stations intended to serve and the required system performance. Equal reception level contours define the size of a cell, and they should be drawn to make overlapping minimum. In this project we assume a flat terrain where the base stations are located in a regular hexagonal arrangement. Although the real footprint has an irregular shape as described before, a regular cell shape is needed for systematic design. A circle footprint is the ideal case, but we cannot draw a map of adjacent circles without leaving blank spaces or overlapping areas. If we compare the area of an hexagon, a square and a equilateral triangle, given fixed distance between the center of a polygon and its farthest perimeter point, the hexagon has the largest area of the three. Thus, hexagons closely approximate the ideal circular radiation pattern of an omnidirectional antenna in a free space propagation scenario. 2.1.2. Mobile Stations The term mobile has been traditionally referred to any transmition/reception device that could be moved during operation. Sometimes the difference between mobile (radio terminal attached to a high-speed object such as a vehicle) and portable (radio terminal carried by an user moving at walking speed) is made, but in this project we will not make any distinction between them. We can also call them subscribers, since each user pays a subscription fee to access the system. In some scenarios where traffic handle is important to be analyzed, Poisson model is widely used to describe arrivals in telephone systems, where it may be assumed that the population is infinite. In finite populations, the Bernoulli model is commonly used. This schemes will not be discussed in this project. 2.1.3. Frequency Reuse One of the fundamental reasons why the cellular mobile design is used, is the possibility to manage the available set of frequencies and locate them in a way to minimize co-channel interference. Electromagnetic spectrum is limited in any area, so it must be used wisely by communication systems. Commonly, the cells are arranged in clusters. A cluster is a group of cells that collectively use the complete set of available frequencies [1]. In such a system, the capacity is given by C = M kN = M S (2.1) Where S is the total number of duplex channels available for use, k is the group of channels allocated to each cell, N is the size of the cluster and M is the number of times a cluster is replicated in the coverage area. If the cluster size is reduced while the cell radius is kept constant, more clusters are needed to cover the intended area. This increase the capacity of the system, but it also causes that co-channel cells are located much close together. A formula commonly used to arrange the cells across the field is 2.2 Noise and Interference 9 D= √ 3NR (2.2) Where D is the distance between co-channel cells and R is the cell radius. In the case of several co-channel users in each cell, as it happens to be the scenario studied in this project, the reuse factor is higher than 1. This is often called Space Division Multiple Access (SDMA). 2.1.4. Cell Splitting The cell radius on early cellular systems was as big as several kilometers. These systems are known to be as macrocell systems. Market penetration over the years increased the density of users per area unit, which needed more spectrum available. Therefore, the power of each antenna was lowered, cell radius was decreased, more frequency resources were available in small areas and capacity increased. However, today systems are not uniform, which means that in particular areas within a cell, a disproportionate amount of users can concentrate, generating an un-balance. This situation is solved by the use of microcells, with closely located base stations. In some high demanding scenarios, such as crowded public areas, floors on an office building, the spectrum can be relocated to an even smaller area, named picocell. 2.1.5. Hand-Off Handoff is the series of strategies implemented by the mobile system when an user moves from one cell to another. It is one of the most important tasks of any cellular system: even some systems prioritize handoff requests over phone call initiation. When the user enters a cell, handoff requires the identification of the new base station and the allocation of the voice and control signals to this base station. The handoff threshold should be slightly bigger than the minimum usable signal level. Handoff polices try to maintain an acceptable speech quality along the process, as well as to maintain the concept of the planned cellular network avoiding congestions and without allowing the use of the assigned channels outside their own cell. An analytical traffic model for handoff was studied in [26] and [27]. In this project the mobiles are considered to be moving and short fading is accounted for that, but no long distance movement that could provoke the transference from one cell to another is going to be made. 2.2. Noise and Interference Besides propagation path loss and multipath fading (which are discussed in chapter 4), wireless communications are mainly affected by noise and interference levels. It is interesting to notice that beamforming algorithms respond to noise in a different way as to interference. Noise level may scale the weight vector 2.2 Noise and Interference 10 power, while interference can produce a zero-forcing response in the direction of the interference. 2.2.1. Noise-Limited and Interference-Limited Environment A radio communication link between only two transceiver units is basically affected by thermal noise. If one of the units is in motion, the performance is also affected by multipath fading. This environment type is called NoiseLimited. When several transceiver units are on the field, using co-channels (same frequency channels) or adjacent channels (immediate neighbor frequency channels), and the power of this interference is superior to the noise power, we are on the presence of an Interference-Limited Environment. 2.2.2. Intracell and Intercell Interference Interference can also be classified depending on its source. Given a base station k allocated to a subset of mobiles I(k) and a mobile i, allocated to k and part of I(k). The intracell interference at mobile i is the sum of the signals that k sends to other co-channel users belonging to I(k) received by i. Intercell interference is the sum of signals from co-channel users outside I(k). This notation is used along the rest of the project. 2.2.3. Signal to Interference Plus Noise Ratio Signal to Interference Plus Noise Ratio (SINR) is certainly one of the most important performance parameters. In fact, most of the cellular radio resource allocation algorithms that have been developed for handoffs, dynamic channel assignment, power control and beamforming (included the ones proposed in this project) are taken under the assumption that the subscribers and/or the base stations (BSs) have access to real time measurements of the received SINR. However, in-service SINR measurements depend strongly on how the system is set up and tuned, which is often confidential. Chapter 3 Antenna Array Transmitter Isotropic antennas radiate equal quantities of power in all directions, giving a signal strength coverage of the shape of a smooth circle if the terrain is perfectly flat. Because of obstacles and ground level imperfections, the coverage area can adopt an irregular shape, intensifying transmitted power in some points and producing undesired severe interference in others. Besides, if some areas need more transmitted power, the power in a single isotropic antenna element cannot be increased in all directions, due to power limitations and also because of the interference produced in other users. The current demand for better transmission techniques has obliged the development of new antennas and mechanisms that represent an alternative to the use of traditional isotropic antennas. Directional antennas provide a direction in which the antenna has a maximum gain. We can emulate this directivity with antenna arrays, where we can give the proper weight and phase to the signal of each element, combine the signals and make a single output. The beam can be pointed in different directions, giving the possibility of adaptive systems that respond to the high mobility and volume of today communications. In case of adaptive antennas, the gain and the phase of the signals induced on the various elements are changed before combining to adjust the gain of the array in a dynamic fashion, as required by the system. Besides these benefits in gain, directivity and adaptiveness, the advantages of antenna arrays go further, because they allow the identification, selection and representation of signals in complex environments such as mobile communication, radar and other applications. Antenna arrays still remain as a hot issue for research. Developments on conformal arrays and microstrip architectures could set on motion the implementation of receiving antenna arrays in the mobiles, which would allow the employment of MIMO (Multiple Input Multiple Output) mobile communications. Further information on implementation techniques, architectures and models can be found in [22] and [18]. This chapter will elucidate the characteristics of the antenna array scheme used for the signal transmission in this project. First we will study the mathematical model of the Uniform Circular Array (UCA) used, and then, the main 3.1 Antenna Array Model 12 Figure 3.1: Transmission from a mobile to a base station in an urban environment. The base station follows the UCA model. Scattering around the mobile (which will be discussed in the next chapter) creates an angle spread σθ in the signal coming from angle θ features of adaptive beamforming are given. 3.1. Antenna Array Model The antenna array geometry that we are going to use in this project is the Uniform Circular Array (UCA). A simple example can be seen in figure 3.1. Circular arrays are used in applications that require full azimuth coverage. The m antenna elements are assumed to be omnidirectional. Being this a practical model, the array consist of a finite number of elements, therefore they are only an approximation to an ideal continuous circular aperture. In consequence, ripples in phase and amplitude are observed, which can only be put down to an acceptable level if the array radius is calculated to achieve an spacing between the elements just below λ2 . The array response, a(θ) for the UCA, with an incoming far field beam from angle θ is expressed in the following equation: m−1 2πα 2πα a(θ) = ej λ cos(−θ) . . . ej λ cos( m 2π−θ) (3.1) This model is found in [14], and is based on a direction finding excitation. Its simplicity and sensitivity is considerably great. One of its most particular aspects is that, in contrast with linear arrays, the pointing direction of the generated beam is not frequency dependent, but the utilization of phase shifters makes the beamwidth in a small extent frequency dependent. A work in how to 3.2 Beamforming 13 deal with the broadband constant beamwidth beamforming problem for circular arrays is presented on [19]. Antenna arrays can be located in both extremes of the radio link, but in this project we only consider arrays for the base station. The mobile station is assumed to have a single omnidirectional antenna. There is only one array per cell. We use far-field and narrow-band approximation. That is the distances from all mobile stations within a cell to the array allocated to that cell are assumed to be much larger than the distance between the antenna elements, so that all waves reaching the array are planar. Besides, the bandwidth of all baseband signals received from and transmitted to the users is considered to be much smaller than the inverse of the maximum time that a planar radio wave with velocity co of propagation needs to cover the diametral length of the antenna array. 3.2. Beamforming Beamforming is the process in which we give proper weights (in amplitude and phase) to the signals in an array aperture and by combining these signals we can strength the desired output, while filtering out the unwanted interference, and environmental and system noise [4]. It can be applicable to either radiation or reception of energy. The beam points towards the direction in which the array has maximum response and therefore, maximum gain. Generally speaking, beamforming includes the shaping of beam patterns and space diversity combining techniques. Adaptive array beamforming can be dependant on the signal source or constructed as a statistically optimum process. It is able to provide better signal reception as compared with the synthesized array, which always has a set of fixed weights that produces a fixed array response that can be switched in a given set of directions [34]. The beam pattern is the plot of the array response as a function of angle. In any beam pattern we can observe a series of minimums and maximums. The place where the beam pattern drops to a zero value on either side of the beam pointing direction is normally referred to as a null. The pattern between the two nulls on either side of the beam pointing direction is known as the main lobe. The width of the beam (main lobe) between the two half-power points is called the half-power beamwidth. But there can also be found sidelobes outside the main lobe, with local minimums. With an m-element array, you can specify m − 1 different positions or degrees of freedom of the array. If the number of array elements is small, then setting a null to suppress an interference signal can substantially affect the array sensitivity over the intended angular coverage area. By increasing the number of antenna elements we can obtain a higher resolution, but the cost and complexity of the array also increases. That is why in every design, the engineer must deal with the trade-off between the array resolution capability, sidelobe level, and the number of array elements. In this project we choose a minor number of antenna elements mainly 3.2 Beamforming 14 because of limited capacity of computation. In principle, beamforming can be applied to both uplink and downlink, nevertheless there are some conceptual differences. Uplink beamforming can be undertaken independently at each receiver, without directly changing the performance of other links, while downlink beamforming at each transmitter will affect the interference to all other receivers. Hence, while designing downlink beamformers we must concern on the total system gain instead of individual links, because all the different beamformers in a system affect jointly the global performance. 3.2.1. Uplink Beamforming Array antennas help to identify and isolate the uplink signals from different users, decreasing the power control requirements or mitigating the impact of inaccurate power control. Algorithms for uplink beamformers can be found extensively in the literature [4], [22] and [23]. It is assumed that perfect channel information is present for the uplink case. This is possible since the channel may be estimated during reception. Most of the solutions take a certain power allocation and calculate the SINR-maximizing uplink beamformer by independent eigenvalue decompositions. In optimal techniques, a cost function is formulated, such that when the cost function is minimized, the quality of the signal is maximized at the array output. Solutions can be found through the application of Minimum Mean Square Error (MMSE) and Least Squares (LS) criteria. 3.2.2. Downlink Beamforming As it has been said before, the downlink is one of the most critical parts of the communication, not only because the transmitter beamforming affects all users within a cell but because of the asymmetry in the data traffic that leads to a capacity bottleneck in the communication from the base station to the terminals. Improvements in downlink performance could be implemented if we allow the subscriber at the end of the link to use spatial processing. But because of limited space, processing power and their dynamic nature, mobile units typically have only one antenna element and can only perform limited spatial processing. However, it is reasonable to assume that the base station is equipped with an antenna array. This is the scheme used in this project: antenna array in the access point and single antenna in the terminals. The main difficulty in downlink beamforming is that, in order to be able to form efficient beams in the cell, the channel between the mobile stations and the base stations has to be known before transmission, while in uplink the channel can be estimated during reception. The channel is more complex and so are the algorithms to estimate it. Also, the other main complication in downlink beamforming is power limitation. When the gain of the antenna array increases towards one specific direction in order to satisfy some user requirement, the total transmitted power must be restrained. Otherwise, excessive gain in one 3.2 Beamforming 15 direction could worse the co-channel interference (CCI) inside and outside the cell, as well as the fact that we should employ a practical power level on the transmitter. Optimal and decentralized downlink beamforming techniques are discussed in chapter 5. Chapter 4 Channel Modeling A channel is a link connecting a transmitter and a receiver in a communication system. As any other physical medium, communication channels are subject to attenuation. In free space, the causes of propagation path loss are only the frequency of the signal transmitted and the distance between transmitter and receiver. Since the signals we are dealing with in this project are mainly ground mobile signals, we must use a ground mobile radio model affected not only by the wavelengths of the propagation frequencies, but by the location of human-made structures and the mobile nature of the receiver. Also, narrowband systems, such as first-generation cellular, are affected by the rapid spatial variation because of interference among the multipath arrivals. In this chapter we give a detailed explanation of the statistical models used to determine the communication channels used during the simulation. First, the important aspects of multipath propagation and fading are considered. Then, the narrowband characteristics of the channel are given, along with its main properties and the mathematical models. Finally, a draft for the channel estimation methods is defined. 4.1. Multipath propagation Radio links in modern wireless systems cover relatively small distances, which allow the implementation of frequency reuse techniques and low radiated power by the antennas. Considering this short distances, and due to the fact that most of mobile units are inside urban areas, the major propagation problems come from obstacles such as buildings and built-up structures. In such an environment, direct line of sight between the base station and the antenna of the mobile unit is quite difficult. Instead, buildings act as scatterers and the signal can diffract around them (in cities where antennas are considerably below the building rooftops), over them (medium and low height buildings) or both (mixed height buildings). Scattering causes that two or more attenuated versions of the transmitted signal can reach the antenna receiver through different 4.2 Fading 17 paths from different arriving directions. The difference between the path lengths of incoming radio waves generates a differential time delay which introduces a phase shift between the components of the signals. These components add up together either constructively or destructively. In consequence, the effects of the multipath propagation can be seen as a path gain. Because of reciprocity, the path gain is still the same no matter if the transmitter is located at the base station antenna and the mobile is receiving, or vice versa, given that the transmission is at the same frequency. If we also consider a mobile receiver, traveling with a constant velocity, path length will change according to its position and the impact of the different incoming components will be of time-varying nature. The amplitude of the received signal will fluctuate and in some locations there will be high constructive addition, while almost absolute cancellation in others. This phenomenon is called fading and it will be detailed in the next section. There can be a random frequency modulation due to varying Doppler shifts on the different multipath signals. The Doppler spreading of the received signal increases the signal bandwidth. The delay power spectrum describes the intensity, averaged over the fading fluctuations, of the scattering process at some given propagation delay. We can take two statistical moments out of this function and use them for our own interest, and they are the delay spread and the Doppler spread. The delay spread appears because the mobile receives several delayed copies of the same transmission, generating a spreading of the signal in time. Typical values for delay spread range from a fraction of a microsecond in urban areas to something on the order of 100 seconds in a hilly area, which restricts the maximum signal bandwidth between 40 and 250 kHz [2]. The reciprocal of the delay spread is defined as the coherence bandwidth of the channel, denoted by Bc . In the same way, the reciprocal of the Doppler spread is a measure of the coherence time of the channel, which is denoted by τc . These two parameters characterize the nature of the channel. In this project we will assume frequency flat communication channels, since in mobile radio transmissions the message bandwidth is very small compared to the coherence bandwidth of the channel. 4.2. Fading Fading is used to describe fluctuations in amplitude, phase and multipath delays of a radio signal over a short period of time or travel distance. It is caused by the multipath propagation explained in the previous section. Fading is highly dependant to the relation between the signal parameters (such as bandwidth, symbol period, etc.) and the channel parameters (such as delay spread and Doppler spread). We study only the cases that concern us in this model: large scale fading and small scale fading. 4.3 Narrowband channel model 4.2.1. 18 Large Scale Fading Large scale fading is mainly caused by terrain configuration and represents the average signal power attenuation or the path loss resulting from motion over large areas. The receiver is often said to be shadowed by prominent terrain contours such as hills, forests, billboards, or clumps of buildings in the path between the transmitter and receiver. The statistics of shadow fading used in this project are described in terms of a mean-path loss, proportional to r1α (where r is the distance between the base station and the mobile station, and α is the path-loss exponent, often in the range 2 ≤ α ≤ 4), and a log normally distributed variation around the mean (with variance σsf ). 4.2.2. Small Scale Fading Small scale fading causes rapid changes on the channel impulse response within the symbol duration, and is caused by multipath reflections of a transmitted wave by local scatterers. If the line of sight between transmitter and receiver is obstructed, the envelope of the received signal behaves like a Rayleigh distribution, and the channel is said to be a Rayleigh fading channel. Otherwise, if there are fixed scatterers and the main propagation path is strong enough, the Rayleigh model is inaccurate and a Rician distribution is more appropriate. 4.3. Narrowband channel model A mobile radio channel can be modeled as a linear filter with a time varying impulse response, where the time variation is given by the changing mobile spatial position. We will give first a simple model with a single transmitted signal from one base station to a mobile station. Using the notation in [28] and [8], the transmitted bandpass signal can be represented as s(t) = Re s̃(t)ej2πfc t (4.1) Where s̃(t) is the complex valued low-pass envelope of the transmitted signal, and fc is the carrier frequency. Due to the multipath effects mentioned in the previous section, the channel has a delay-dependant and time-varying impulse response, and its function can be expressed as h(τ ; t) = Re h̃(τ ; t)ej2πfc t (4.2) h̃(t) is the low-pass complex valued impulse response of the channel, also known as the input delay-spread function, and τ is the delay variable. We assume that the multipath signal received at time t consists of the sum of components that have followed L different paths, where L is very large due to reflections, diffractions and scatterings in the close vicinity of the mobile. Typically, the scatterers are uncorrelated and therefore the function h̃(t) can be modeled as a zero-mean complex-valued Gaussian process and the channel will be from now 4.4 Multiple users and multiple antennas 19 on referred as the Rayleigh fading channel. The received signal, for t > 0 will be: ∞ r(t) = h(τ ; t)s(t − τ )dτ + n(t) (4.3) 0 Here, n(t) is the additive white Gaussian noise with distribution N (0, σ 2 ). In typical mobile radio transmissions, the signal bandwidth is very small compared to the reciprocal of the spread in propagation path delays. Hence, we can assume that there is no time dispersion at all and h(τ ; t) = 0 for τ = 0. Based on the Nyquist-Shannon theorem, the discrete received signal is then r(t) = h(t)s(t) + n(t), t > 0 (4.4) Even though we will use the narrowband representation in this project, reallife signals with digital signalling may occupy a wider bandwidth. 4.4. Multiple users and multiple antennas If the model is extended for a cellular mobile communication environment with K base stations composed by m antenna elements carrying out a synchronized transmition to d mobiles sharing the same spectrum resources, the baseband signal ri (t) received at mobile i is given by ri (t) = K h∗i,k xk (t) + ni (t) (4.5) k=1 In this case, xk (t) is the vector of signals transmitted by the antenna elements at the base station k and hi,k ∈ Cm is the vector channel from base station k to mobile i. The vector xk (t) is given by xk (t) = wi si (t) (4.6) i∈I(k) wi ∈ Cm is the beamforming vector that gives the proper weight to the modulated signal si (t) intended for mobile i. We will assume through the whole project that si 2 = 1. Therefore, the downlink transmission powers will be included in the beamformer vectors. To give more clarity we can express the downlink beamformer vector as wi = √ pi ui (4.7) Where pi is a scalar that provides the proper weight to the normalized space filter ui of length m. In the same way, the uplink beamformer can be expressed √ as wi = q i ui , without losing generality. The downlink beamforming algorithms that we use in this project will determine both the power control and 4.5 Downlink Channel Estimation 20 the spatial filtering jointly. However, some solutions have been developed that separate these procedures, and after the ui vectors are found, a standard power control scheme is applied. Further reading in this convergence method can be seen in [8]. When we say that mobile i belongs to I(k), we specify that the mobile is allocated to the base station k. From now on, the notation I(k) is used for users inside the same cell. In the same way, κ(i) refers to the base station allocated to mobile i. A mobile station can be allocated only to one base station at a time, since we do not consider soft handover situations. 4.5. Downlink Channel Estimation Given all the assumptions that we have mentioned so far, and applying the knowledge we have about multipath propagation and fading, we can express the formula for the Rayleigh fading uplink channel as the sum of L reflected paths of a plane wave with frequency f from a source located at an angle θ(t) arriving into a given antenna array with array response a(θ; f ). The array is supposed to be calibrated, and conditions for downlink and uplink are the same. It is possible to write the uplink channel vector from a mobile to a base station as hup = L γlup a(θlup ; f up ) (4.8) l=1 Here, γlup is the complex-valued amplitude coefficient for each path. The array response is defined according to the topology of the antenna array. In this project we use the expression formulated in (3.1). For the downlink case we have hdown = L γldown a(θldown ; f down ) (4.9) l=1 In Time Division Duplex (TDD) systems, the uplink and downlink transmission shares the same frequency using different time slots. If the delay between the uplink and downlink time slots is small compared to τc (coherence time of the channel), the signature of the downlink is identical by reciprocity to that of the uplink. In such case, we can assume that θlup = θldown and γlup = γldown , so the instantaneous uplink channel can be used as a good estimate of the downlink channel. Hence, the correlation matrix defined as Ri,k = hi,k h∗i,k will have rank one. When the duplex separation is larger than the coherence time of the channel we can not make instantaneous characterization, but it is still reasonable to assume θlup = θldown and E[|γlup |2 ] = E[|γldown |2 ]. Thus, we have access to the channel correlation full-rank matrix Ri,k = E[hi,k h∗i,k ]. It is convenient to express Ri,k as inversely proportional to the square distance between the mobile and the base station and proportional to the covariance matrix Ra (θ). 4.6 Feedback 21 An equation for the matrix Ra (θ) of size k, l in an Uniform Circular Array (UCA), was presented in [29] and it is given as j Ra UCA ,kl (θ) = e 4πα λ k+l−2 sin(π k−l −θ) − n ) sin(π n e 2 σa 2 k−l k+l−2 ( 4πα −θ) λ sin(π n ) cos(π n (4.10) Since the scatterers are spread, the signals reflected from the mobile arrive at the base station at angles that are Gaussian distributed around the straight line of sight from the transmitter to the receiver. This scattering effect can be modeled by an angular spread with a fairly small variance σa2 . In systems with Frequency Division Duplex (FDD), the frequency gap between up and downlink often surpasses the coherence bandwidth Bc of the channel and therefore, uplink channels fade independently from downlink channels. If we consider the channel covariance matrix averaged over the fast fading, we can still get good performance. However, there are more sophisticated strategies for channel estimation, which use training data, feedback channel from the mobile, Capon method, etc. 4.6. Feedback Control channels in communications systems are often available to implement power control, adaptive modulation, and certain closed-loop diversity modes. Using this fact, the transmitter can use feedback from the receiver to exploit channel conditions and avoid interference. Usually, feedback is severely limited, so it is important to determinate how to quantize the information needed at the transmitter and how much improvement in performance can be achieved as a function of the amount of feedback available. A feedback strategy between base station and terminal in a communication system starts when the base station transmits a pilot sequence to the mobile station. The receiving mobile use this sequence to calculate the feedback information. This information is immediately sent back to the base station. Then, the base station uses the feedback information to estimate some Quality of Service (QoS) parameter, for example the Signal to Noise Ratio (SNR), which will the input of the downlink beamforming optimization problem. Next, the base station chooses a communication rate capable to fulfill the capacity outage probability (given the SNR estimation and its statistics). Finally, the base station uses the remaining symbol times to data transmission. The receiver fixates its own uplink beamformer such that its SNR estimation will be maximized. Alternative channel estimation methods taking advantage of space-time coding feedback strategies were shown in [32] and [33], which prove that the downlink Channel State Information (CSI) can be quantized and sent to the transmitter over a limited-rate feedback channel, though losing some eigenstructure. This project will not use transmitting diversity and we will consider the downlink channel to be inferred from the uplink channel. However, some special parameters of the received signal at the mobile can be sent back to the base 4.6 Feedback 22 station, such as statistics on the signal power, interference and quality measurements. Chapter 5 Downlink Beamforming Algorithms As it has been said before in this report, the literature on uplink beamforming is extensive. Different uplink beamforming techniques developed over the years can be found in [3, 4, 20, 22, 23, 30]. However, downlink beamforming has not been so widely investigated. In [5], multiuser downlink beamforming is formulated as an optimization problem where the weight vectors for different mobile stations are jointly optimized in order to satisfy given SINR threshold specifications in each mobile, while minimizing the total power transmitted from the base station. This is a quadratic optimization problem with quadratic nonconvex constraints. Different solutions have been presented (see [8] for an overview). The problem was solved for the first time by Rashid-Farrokhi et.al. [6] who presented a generalization of the standard power control algorithm which attains an optimal and feasible set of transmit beamforming vectors if there exist any. Several solutions based on the duality between uplink and downlink channels have been built to iteratively obtain the optimal downlink beamforming vectors. Some results can be found in [10], [11] and [12]. Nevertheless, the convergence behavior of this algorithms is slower as the SINR requirements become more stringent. A transmit strategy was specified in [9], where it was shown how the optimal downlink multiuser beamforming optimization problem can be relaxed using semidefinite programming and still being able to find the optimal solution. This procedure was adapted in [13] where the downlink beamforming weight vectors of different MSs are jointly optimized in their corresponding subspaces, instead of searching through the entire parameter space. The resource allocation algorithms mentioned above require global knowledge of channel statistics and may be used in the search for the fundamental performance limits of a wireless system. In order to diminish signalling between base stations, reduce number of operations and decentralize the solution of the problem, we have developed new techniques with reduced feedback from the mobile. The base stations will be required to have access to channel knowledge 5.1 Optimal Beamforming 24 only within their own cells and find feasible solutions to their allocated users. In this chapter we first review the optimal beamforming, based on the fact that the system should provide an acceptable quality of service at the less cost, while serving as many users as possible. We use this as support for our own techniques, which is also explained and detailed. Performance results and comparisons between methods are deployed in a separate following chapter. 5.1. Optimal Beamforming There are many ways to define optimal beamforming. We adhere to the scheme proposed in [5], based on the operators perspective. The system must provide a certain Quality of Service (QoS) to as many users as possible with a low cost. The user requirement on QoS is assumed to be fulfilled if the Signal to Interference Plus Noise Ratio (SINR) on the received signal at the user terminal i exceeds the threshold γi , specified for every terminal i. It is worth to notice that different users can demand different QoS requirements, depending on the resources they need. Thus, a system must be able to satisfy different SINR thresholds on every user. From (4.5) and (4.6) we can derive a more complete expression for the received signal as h∗i,κ(n) wn sn (t) + ni (t) (5.1) ri (t) = h∗i,κ(i) wi si (t) + n=i desired signal noise interference As it can be seen, base station κ(i) modulates signal si (t), gives a proper weight wi (t) to it for each antenna element, and then transmits through channel hi,κ(i) . But this signal is affected by the transmission of signals intended for other users through the channels between all the base stations and mobile i. If we want the SINR in such mobile to surpass the constraint γi , and assuming that the base stations transmit each symbol simultaneously in burst synchronization, then the system must fulfill the expression wi∗ Ri,κ(i) wi 2 ≥ γi ∗ n=i wn Ri,κ(n) wn + σi (5.2) Where the scalar σi2 is the noise power received at user i and γi is the target SINR for user i. 5.1.1. Joint Optimal Beamforming and Power Control Optimal beamforming consists in the design of the set of beamformers wi , given estimates of all the channel correlation matrices Ri,κ and noise levels σi2 . The goal is to minimize the total transmitted power while providing sufficient received SINR at each terminal. The problem may be formulated as 5.1 Optimal Beamforming 25 min d wn∗ wn n=1 subject to wi∗ Ri,κ(i) wi∗ ≥ γi wn∗ Ri,κ(n) wn + γi σi2 (5.3) n=i A series of important observations around this optimization problem were made in [31], and they are: 1. The cost function in (5.3) is continuous and coercive, its value converges to +∞ along any sequence of its arguments such that the norm of the arguments also converges to +∞. Because the set of constraints is not empty and a feasible solution exists, then, by the Weierstrass’ Theorem, a global minimum exists. 2. For the optimum wi , all constraints hold with equality. This can be shown by contradiction: if there is a global minimum with strict inequality constraint i in (5.3), then wi 2 can be scaled down without violating the constraints. Thus, we can still get a feasible point with a cost function value smaller than the global minimum, which is a contradiction. 3. If the constraints in (5.3) are normalized with respect to the noise level, an equivalent normalized downlink optimization problem is obtained. There are two kinds of algorithms solving (5.3), namely, duality-based and semidefinite programming solutions 5.1.2. Duality-Based Algorithms The duality between uplink and downlink channels was first established in [6]. It is possible to construct a virtual uplink network whose channel responses are similar to that of the downlink. After the receiver beamformer vectors at the base stations of the virtual uplink are found, the same combining vector were used at each iteration for the downlink. The uplink power allocation and beamforming vectors converge to a constant (optimal) power allocation, which makes that the uplink gain matrix converges to a fixed matrix whose eigenvalues are inside the unit circle. Using the fact that the eigenvalues of the gain matrix in the downlink and uplink are the same, the downlink iteration is convergent if the virtual uplink is so. In consequence, under the constraint of equal receiver noise, both uplink and downlink have the same SINR achievable region. Nevertheless, in case of different receiver noise levels, the problem remains optimal if the channel covariance matrices are scaled by the noise variances. An iterative strategy for minimizing the expense of transmission power while proving feasibility was derived in [12]. Also, a similar approach with congestion control was achieved in [7]. 5.1 Optimal Beamforming 5.1.3. 26 Semi-Definite Programming and Convex Optimization In [9] the same optimization problem was considered, presenting an alternative solution using convex optimization. A convex optimization problem is the minimization of a convex function over a convex set. The local minimum of a convex function is also the global minimum, which means that there are no other local minima which the minimization can be forced in. During the last decade, convex optimization techniques, specially semidefinite programming and second order cone programming, have become one of the most significant innovations in the area of mathematical optimization, finding applications in multiple disciplines such as control theory and signal processing. The basic beamforming problem (5.3) is a quadratic optimization problem with quadratic nonconvex constraints, which in general could be a NP-complete problem that cannot be solved in reasonable time. However, for the special case of rank one channels, where Ri,κ = hi,κ hi,κ ∗, (5.3) can be written as follows: min d wn∗ wn n=1 subject to |wi∗ hi,κ(i) |2 ≥ γi wn∗ Ri,κ(n) wn + γi σi2 n=i Im wi∗ hi,κ(i) = 0 (5.4) wi∗ hi,κ(i) ≥ 0 i = 1, . . . , d Which turns out to be a convex problem because the constraints for each i are just an affine transformation of the convex second-order cone (x, y)x ∈ R, y ∈ CN , x ≥ y Therefore, the problem can be solved using the convex optimization techniques. A rank-relaxed approach is shown in [9], which provides larger flexibility. It is worth notice that by this method, called Lagrangian relaxation, sometimes we cannot obtain rank-one wi but high-rank solutions that can be taken as a correlation matrix for the beamformers. 5.2 Decentralized Algorithms 5.2. 27 Decentralized Algorithms The optimal algorithms explained before require full Channel State Information (CSI) inside and outside the cell. A decentralized algorithm takes the original optimization problem in (5.3) and solve it for each cell separately. As it is obvious, the joint power control and beamforming is not possible in this approach, therefore it is a suboptimal solution, though it can still give good performance. The constraints specified in (5.2) are of the form S ≥ γi Iintra + Iinter + N (5.5) Where S denotes the power of the desired signal, Iintra and Iinter represent the intracell and intercell interference, respectively, and N is the noise power. When channel allocation at base stations is made without global coordination, even though we might still be able to estimate the intracell interference on each base station, the intercell interference can no longer be accurately estimated. In consequence, the earlier assumption that the total interference can be accurately predicted at a given subscriber needs to be reconsidered. In the following sections, we will formulate different ad-hoc strategies used to handle the intercell interference. 5.2.1. Increased SINR Margin Consider a base station κ which has CSI knowledge of all mobiles inside its own cell, but no information available about the channels in exterior cells. The simplest strategy consists on ignoring the intercell interference term and increase the SINR margin by a factor β > 1, and establish some new constraints S Iintra + N ≥ βγi (5.6) These constraints change the optimization problem, so (5.5) will remain true as long as (5.6) holds for a β that fulfills the condition β≥ 1 1 − γi Iinter S (5.7) Under the assumption that β ≥ 1, the following condition must be also true 1 Iinter ≤ S γi (5.8) Therefore, one way to determine β is to collect statistics of the quotient Iinter /S and choose a β such that (5.7) holds under a certain upper bound. Statistics of Iinter /S can be sent to the base station from either the central resource manager or the same mobile, given that the latter has a certain signal processing capacity. Anyway, the amount of information sent is reduced to only a scalar per mobile, turning into a very reduced feedback model. The algorithm 5.2 Decentralized Algorithms 28 works with only the 90 percentile value of Iinter /S averaged over a fairly long time period, so the feedback rate is very low. However, the time window in which we take the average must be inferior to the coherence time of the channel. Since Iinter /S vary when changing β, a few iterations may be needed. Then, it is important to prove convergence. A work sequence for the iterations is detailed in table 5.1. 1. β = 1 2. repeat 3. solve (5.6) 4. send Iinter (90% averaged value) → S base station 5. β old = β 6. from (5.7) → β̂ 7. new β = β̂ 8. until β old = β̂ Table 5.1: Increased SINR algorithmic solution 5.2.2. Penalty Term When we increase the SINR constraints, the main lobe of the beam pattern is increased in power, but also are the sidelobes. Higher sidelobes means higher transmitted interference to other users, both inside and outside the cell. It is also a waste of energy. The idea here is to add a penalty term in the denominator of the SINR constraints to reduce the risk of high sidelobes on the beamformers min d wn∗ wn n=1 subject to |wi hi,κ |2 ≥ βγi , 2 2 2 n∈I(κ) |wn hi,κ | + σi + αwi ∀i ∈ I(k) (5.9) n=i Which reduces to (5.6) when α = 0. It can be argued that the cost function itself already tries its best to keep all wi 2 as small as possible and it is clear that increasing α will increase the total transmit power, since we make the constraints more strict, but the power will be concentrated on the main lobe. However, it might be possible to use a lower value of β, so the system performance might benefit. An algorithmic solution is shown in table 5.2. 5.2 Decentralized Algorithms 29 1. β = 1, α > 0 2. repeat 3. solve (5.9) 4. send Iinter (90% averaged value) → S base station 5. β old = β 6. from (5.7) → β̂ 7. new β = β̂ 8. until β old = β̂ Table 5.2: Penalty Term algorithmic solution 5.2.3. Additional Constraints Assuming that mobiles have only one omni-directional antenna, the sum of all the energy received by the base station κ in the uplink is of the form y(t) = d qn hn,κ sn (t) + n(t) (5.10) n=1 Where qn hn,κ sn is the uplink signal sent from the mobile n to base station κ. User n can be either inside or outside the cell. This expression contains CSI from the base station κ to all the mobiles. As strong channels can be recognized at the base station, far-away channels will be negligible respect to the closest ones. Once the channel allocation is made, the base station is able to determine the estimate of the channel vector, viewed just as a complex valued vector, of the Signal Of Interest (SOI), and obtain the value of the signal. As well, the rest of the channels allocated to the base station can be discerned from all the information received. If we subtract the estimate of the SOI from (5.10) we have ỹ(t) = y(t) − h̃i,κ(i) s̃i (t) (5.11) Given the channel reciprocity between uplink and downlink data, we can manipulate (5.11) to obtain statistics about the estimate of the interfered channels through a certain period, which can be expressed as Q̂i = N 1 ỹ(t)ỹ(t)∗ ≈ qn E hn,κ(i) h∗n,κ(i) + σn2 I N t=1 (5.12) n=i In the numerical examples, the statistical moment E[hn,κ(i) h∗n,κ(i) ] can be taken 5.2 Decentralized Algorithms 30 from the expression formulated in (4.10), and then (5.12) becomes qn Ra,n + σn2 I Q̂i = (5.13) n=i Where Qi are positive semidefinite matrices. When we normalize respect the channel between the base station and the mobiles, the scalar values qn can be expressed as qn ∝ 1 (5.14) hn,κ(i) 2 The estimates of Qi , based on uplink measurements, can be used to actively suppress interference to mobiles in other cells that have a strong channel to the base station in the form of constraints to the downlink optimization problem as min d wn∗ wn n=1 subject to |wi hi,κ |2 2 ≥ βγi , 2 n∈I(κ) |wn hi,κ | + σi ∀i ∈ I(k) (5.15) n=i wi∗ Qi wi ≤ μi , ∀i ∈ I(k) In consequence, this strategy tries to predict the interference caused at the particular users in the surrounding cells that will suffer the most from our transmitted signal. The scalar factors μi are positive constants used as a constraint for the interference produced by the base station towards the specific users that we heard most clearly when they transmitted in the uplink. A large μi would mean a entire liberty for the beamformer and therefore no constraint at all, while a very small μi might produce an unfeasible scenario. A scheme for the solution can be seen in table 5.3 5.2 Decentralized Algorithms 1. β = 1, μi > 0 2. repeat 3. solve (5.15) 4. send Iinter (90% averaged value) → S base station 5. β old = β 6. from (5.7) → β̂ 7. new β = β̂ 8. until β old = β̂ Table 5.3: Additional Constraints algorithmic solution 31 Chapter 6 Simulations and Performance Study The decentralized algorithms were tested in a simulation environment. In this chapter we will discuss in depth the simulation conditions and the results obtained. We will prove the convergence of the solutions, study some characteristics about the interference handling in each algorithm, compare the beam patterns obtained and show the overall performance in the simulated scenarios. The simulations are intended to show the behavior of the proposed algorithms. They do not aim to evaluate performance in a complete system. In order to do this, further assumptions on multiple access scheme, modulation and coding would be needed. The interplay between spatial processing and time/frequency processing is beyond the scope of this project. 6.1. Simulation Environment The multi-cellular system is simulated with uniform circular arrays at all access points, distributed as a regular hexagonal cell-divided area as in figure 6.1. In order to ignore edge effects, the model contains 19 cells so that the analysis could be made only in the 7 most inner cells without losing generality. Mobile stations are spread over the cells in an uniform distribution. The user load per cell is exactly the same number of users in each cell and is varied among simulations. Mobiles are allocated to the strongest channel with the base stations. We express the communication channel vectors as a function of the angle between the mobile and the base station and the standard deviation of the angular spread. All the assumptions regarding multi-path propagation and frequency flat Rayleigh fading channels detailed earlier in this report hold for the simulations. Fast fading is supposed to be normally distributed. The channel gain is affected by the distance dependent path loss with path loss exponent αatt and the log-normally distributed shadow fading. 6.2 Results 33 Number of scenarios Number of simulated cells Number of evaluated cells Reuse factor Maximum load per cell (users) Noise level SINR Number of antenna elements Uniform circular array radius Number of paths in propagation Shadow fading standard deviation Average path loss Angular spread variance 300 19 7 1 3 0 dB 10 dB 8 λ 3 30 8 dB 3.5 3 degrees Table 6.1: Simulation Parameters The optimal solution is generated according to (5.4), which generates both the power expression and the space filtering jointly. The different decentralized algorithms are executed following the instructions specified in the previous chapter. For the convex optimization calculus, we use the freely available package cvx, developed by Michael Grant, Stephen Boyd, and Yinyu Ye at Stanford University. This software turns Matlab into a modeling language, allowing constraints and objectives to be specified using standard Matlab expression syntax. A summary of the simulation parameters used can be seen in table 6.1. 6.2. Results The figures 6.2, 6.3 and 6.4 show the convergence of the parameter β in the different decentralized algorithms proposed in this project. For the Increased SINR solution, we can see that the convergence is different to that we had expected. β seems to decrease when the number of users per cell is increased to 3, defying our initial guess. By looking at figure 6.5 we also see that the quotient between the intercell interference and the signal is really high in this case, so (5.8) does not hold for the simulated system when there are two or more users per cell. Since the base station does not know anything about the intercell interference level at the moment the beamformers are being solved, the algorithm tries a different value of β that is not correct. This problem extends itself to the other algorithms, since in all of them we have worked with the increased SINR. We can see in figure 6.6 that, for the Penalty Term algorithm, (5.8) holds approximately for one or two users per cell, and the convergence of β fulfills our expectancies (that β increases as we increase the number of interferers). This logic seems to be confirmed when we observe 6.2 Results 34 15 Base Station Mobile Station 10 5 0 −5 −10 −15 −15 −10 −5 0 5 10 15 Figure 6.1: Cellular environment simulated model: 2 users/cell case Figure 6.7, where (5.8) holds for all cases and β converges as we expected. The reason is that the Additional Constraints algorithm is the only algorithm in which the base station have certain control over the intercell interference and it is capable to keep it under a certain value. Next, figures 6.8 and 6.9 show how we varied the main parameters while we kept fixed the cell load. In figure 6.8, we consider different values of α to be included in (5.9) as a control for sidelobes level. Evaluating the percentage of successful users, that is mobiles where SINR≥ γi , we see that the performance gets worse as we increase the value of α. But a too small value for α it is also a bad choice and might affect the way the beamformers are calculated, since the cvx tool is susceptible of errors when dealing with quantities close to 1/4 and can not reach convergence. In the case of the Additional Constraints algorithm, the best choices for the scalars μi were in middle values (20 ≤ μi ≤ 50), as it was proved in figure 6.9. Small μi would mean too tight constraints in the solution (5.15) that could lead to infeasibility, while an extremely big μi gives complete freedom to the algorithm, causing the interference to be not restrained at all, ending up with a scheme similar to the one in (5.6). An example of the beam patterns solved by the algorithms can be seen in figures 6.10, 6.11 and 6.12. It is clear that the optimal solution places nulls in the direction of the interferers and places the mainlobe in the optimal angle where 6.2 Results 35 less users are affected. The decentralized algorithms couple the beamformers with the user of interest channel, so the mainlobe points straight to the angle θ where the user is located. In the specific case plotted in the mentioned figures, the mobile of interest i is located at θi ≈ −50◦ and there is an interferer j inside the same cell at θj ≈ 40◦ . As we can see, all the algorithms approximate to the zero forcing solution for the mobile j, placing a null in that direction. But the optimal algorithm is the only one that, taking advantage of the global channel knowledge, can place m − 1 zeros in the interfering directions. For the Increased SINR and Penalty Term strategies, the nulls can be placed only towards interferers inside the same cell. In figure 6.13, it is shown how the power is controlled by the decentralized algorithms, specially for the case of Additional Constraints. However, this power optimization fails when we analyze the outage probability, which was plotted in figure 6.14. An optimal beamforming outage probability equal to zero is only possible in the simulation where a solution for the convex optimization problem expressed in (5.4) is always possible to find. Since calculation capability was put to the maximum during simulations, an optimal scheme as this would not be practical in real systems. But assuming an almost infinite computing capability, the strength of the convex optimization algorithm is still remarkable. The decentralized algorithms outage probability was somehow poorer than expected. Since we applied the increased SINR in all algorithms, a choice of β that fulfills the assumption (5.7) for 90% of the cases, was supposed to drive a similar outage around 0.1, as long as all previous assumptions were also fulfilled. A close value to 0.1 was obtained for the case of one user per cell, but the performance diminishes dramatically as we increase the number of users. The reason why Increased SINR strategy seems to be performing better than the other algorithms is just because this algorithm finds more feasible solutions than the others, more restrictive. When the intercell interference constraints can not be fulfilled for the Penalty Term and Additional Constraint algorithms, the scenario is treated as a whole unfesible problem and no mobile is served. Since the problem is solved in each base station, an unfeasible constraint means a cell shut down. 6.2 Results 36 2.4 1 user/cell 2 users/cell 3 users/cell 2.2 2 β 1.8 1.6 1.4 1.2 1 0 2 4 6 8 Number of iterations 10 Figure 6.2: Convergence of β for the Increased SINR Algorithm 1.4 1 user/cell 2 users/cell 3 users/cell β 1.3 1.2 1.1 1 0 2 4 6 8 Number of iterations 10 Figure 6.3: Convergence of β for the Penalty Term Algorithm 6.2 Results 37 3 1 user/cell 2 users/cell 3 users/cell β 2.5 2 1.5 1 0 2 4 6 8 Number of iterations 10 Figure 6.4: Convergence of β for the Additional Constraints Algorithm −2 1 user/cell 2 users/cell 3 users/cell −4 Iinter/Signal dB −6 −8 −10 −12 −14 −16 −18 0 2 4 6 8 Number of iterations 10 Figure 6.5: Convergence of Iinter /S for the Increased SINR Algorithm 6.2 Results 38 −6 1 user/cell 2 users/cell 3 users/cell Iinter/Signal dB −8 −10 −12 −14 −16 −18 −20 0 2 4 6 8 Number of iterations 10 Figure 6.6: Convergence of Iinter /S for the Penalty Term Algorithm −9 1 user/cell 2 users/cell 3 users/cell −10 Iinter/Signal dB −11 −12 −13 −14 −15 −16 −17 0 2 4 6 8 Number of iterations 10 Figure 6.7: Convergence of Iinter /S for the Additional Constraints Algorithm 6.2 Results 39 40 % Succesful Users 35 30 25 20 15 10 5 −3 −2 −1 0 log10(α) Figure 6.8: Performance of the Penalty Term Algorithm when the parameter α is varied % Succesful Users 44 42 40 38 36 34 0.5 1 1.5 2 log10(μi) 2.5 3 Figure 6.9: Performance of the Additional Constraints Algorithm when the constraint μi is varied 6.2 Results 40 40 θ Optimal BF Increased SINR Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 50 Degrees 100 150 Figure 6.10: Beam pattern for one mobile solved by the Increased SINR algorithm, compared to the Optimal Beamforming 40 θ Optimal BF Penalty Term Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 Degrees 50 100 150 Figure 6.11: Beam pattern for one mobile solved by the Penalty Term algorithm, compared to the Optimal Beamforming 6.2 Results 41 40 θ Optimal BF Additional Constraints Power (dB) 30 20 10 0 −10 −20 −150 −100 −50 0 50 Degrees 100 150 Figure 6.12: Beam pattern for one mobile solved by the Additional Constraints algorithm, compared to the Optimal Beamforming Optimal BF Increased SINR Penalty Term Additional Constraints 80 Power in dB 60 40 20 0 1 2 Number of Users 3 Figure 6.13: Transmitted power for each algorithm according to the number of users per cell 6.2 Results 42 Optimal BF Increased SINR Penalty Term Additional Constraints 1 Outage Probability 0.8 0.6 0.4 0.2 0 1 1.5 2 2.5 Number of Users 3 Figure 6.14: Outage Probability of each algorithm according to the number of users per cell Chapter 7 Conclusions In the majority of the cases, channel state information will be available only in the way of statistical data of spatial correlations. This may be helpful when the channel varies rapidly, but it is not so accurate when it is used to exploit strong channel links such as a fixed or a slowly varying channel. The constraints and modifications made to the original downlink beamforming problem were able to be assembled as convex optimization problems and proved to achieve convergence. Following a series of decentralized algorithms that do not require global channel information, the base stations can find a set of weight vectors that place nulls towards local interferers as well as try to control the intercell interference level. The convergence for parameters as β, α and μ inside each of the algorithms, suggests the idea that every cellular network can be characterized with its ad-hoc values. Furthermore, we can generalize the solution and a network with determined characteristics could use a set of pre-fixed parameters obtained by simulation. However, all algorithms require the existence of a feasible solution. When the cell load increases and too many mobile terminals want to communicate at the same time using the same co-channel, there is a risk that a solution to the optimization problem for all local users may not exist. In this scenarios, the optimization problem must be reduced: access to the system should be denied to some mobiles in order to improve performance. Therefore, a possible future work consists in solving the problem of admission control, that is how to admit or remove mobiles in the system. Without this congestion control implementation, it is hard to say whether the proposed techniques can be used in the real field. We can see that adding constraints to the decentralized algorithm does not offer any advantage, since these constraints do not operate actively in the beamformers. That is a valid set of beamformers can be found that fulfill these constraints, and yet the SINR problem is still suboptimal. A re-formulation of the issue could be needed. Finally, we remember that these techniques are just a part of a bigger problem, which includes all the mobile communication network services. The proposed algorithms, based on a Space Division Multiple Access (SDMA) strategy, 44 are not the only way to guarantee the service towards users. As it was explained along the project, there are plenty of choices. As a SDMA technique, it could be interesting to study in which way the angular separation between users can affect the performance of these algorithms, factor that was not accounted during this project since we worked with random location scenarios. It is the job of researchers and innovators to develop and test new technologies that can overcome this difficulties and grant a better service in mobile communication networks. Bibliography [1] T. S. Rappaport. Wireless Communications. Principles and Practice Second Edition. Prentice Hall. 2002. [2] L. C. Godara. Applications of antenna arrays to mobile communications. I. Performance improvement, feasibility and system considerations. Proceedings of the IEEE. Vol. 85, No. 7, July 1997. [3] ——. Application of Antenna Arrays to Mobile Communications, Part II: Beam-Forming and Direction-of-Arrival Considerations. Proceedings of the IEEE. Vol. 85, No. 8, August 1997 7, July 1997. [4] ——. Smart Antennas. CRC Press. 2004 [5] C. Farsakh and J. A. Nossek. Channel allocation and downlink beamforming in an SDMA mobile radio system. 6th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 1995. Vol. 2, September 1995. [6] F. Rashid-Farrokhi, K. J. R. Liu and L. Tassiulas. Transmit beamforming and power control for cellular wireless systems. IEEE Journal on Selected Areas in Communications. Vol. 16, Issue 8, October 1998. [7] R. Stridh, M. Bengtsson and B. Ottersten. System Evaluation of Optimal Downlink Beamforming with Congestion Control in Wireless Communication. IEEE Transactions on Wireless Communications Vol. 5, No. 4, April 2006. [8] M. Bengtsson and B. Ottersten. Optimal and suboptimal transmit beamforming, Chapter 18 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001. [9] ——. Optimal downlink beamforming using semidefinite optimization. Proceedings of 37th Annual Allerton Conference on Communication, Control and Computing. September 1999. [10] M. Schubert and H. Boche. Solvability of coupled downlink beamforming problems. Proceedings of IEEE Global Telecommunications Conference 2001. Vol. 1, November 2001. BIBLIOGRAPHY 46 [11] ——. A unifying theory for uplink and downlink multiuser beamforming. Proceedings of 2002 International Zurich Seminar on Broadband Communications. February 2002. [12] ——. Solution of the multiuser downlink beamforming problem with individual SINR constraints. IEEE Transactions on Vehicular Technology Vol. 53, No 1, January 2004. [13] N. Wang, P. Agathoklis and A. Antoniou. A subspace multiuser beamforming algorithm for the downlink in mobile communications. IEEE Transactions on Circuits and Systems –II: Express Briefs. Vol. 53, No. 8, August 2006. [14] T. Asté, P. Forster, L. Féty, and S. Mayrargue. Downlink beamforming avoiding DOA estimation for cellular mobile communication. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing. Vol. 6, May 1998. [15] M. Grant, S. Boyd and Y. Ye. cvx User’s guide. January 14, 2007. http://www.stanford.edu/∼boyd/cvx/cvx usrguide.pdf [16] S. Boyd and L. Vandenberghe. Convex Optimization Cambridge University Press. 2004. [17] J. F. Sturm. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Department of Quantitative Economics, Maastricht University, The Netherlands, 1999. http://sedumi.mcmaster.ca [18] R. Mailloux. Phased Array Antenna Handbook Second Edition. Artech House. 2005. [19] Y. Yang, Chao Sun and C. Wan. Theoretical and experimental studies on broadband constant beamwidth beamforming for circular arrays. In Proceedings OCEANS 2003. Volume 3. 22-26 September 2003. [20] Barry D. Van Veen and Kevin M. Buckley. Beamforming - a versatile approach to spatial filtering. IEEE Acoustics, Speech, and Signal Processing Magazine. Vol. 5, No. 4 April 1988. [21] D. G. Brennan. Linear Diversity Combining Techniques. Proceedings of the IEEE Vol. 91, No. 2, February 2003 [22] S. Drabowitch, A. Papiernik, H. D. Griffiths, J. Encinas and B. L. Smith. Modern Antennas 2nd edition. Springer 2005. [23] R. A. Monzingo and T. W. Miller. Introduction to Adaptive Arrays. John Wiley & Sons. 1980 [24] A. R. Modarressi and R. A. Skoog. An Overview of Signal System No. 7. Proceedings of the IEEE. Volume 80, No. 4, April 1992. BIBLIOGRAPHY 47 [25] W. C. Y. Lee. Mobile Communications Design Fundamentals. Second Edition. John Wiley & Sons, Inc. 1993. [26] S. S. Rappaport. Blocking, hand-off and traffic performance for cellular communication systems with mixed platforms. In IEE Proceedings I Communications, Speech and Vision Volume 140, Issue 5, October 1993 [27] M. Rajaratnam. Takawira, F. Hand-off traffic modelling in cellular networks IEEE Global Telecommunications Conference, 1997. GLOBECOM ’97. Volume 1, 3-8 November 1997 [28] B. Sklar. Fading Channels, Chapter 4 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001. [29] E. Björson. Beamforming utilizing channel norm feedback in multiuser MIMO systems Master Thesis, Lund University in cooperation with KTH Royal Institute of Technology, 2007. [30] H. Krim and M. Viberg. Two decades of Array Signal Processing Research: the parametric approach. IEEE Signal Processing Magazine. Vol. 13, No. 4, July 1996 [31] E. Visotsky and U. Madhow. Optimum beamforming using transmit antenna arrays. Proceedings VTC’ 99, IEEE, Houston, TX. Vol 1. May 1999. [32] A. Narula, et. al. Efficient use of side information in multiple-antenna data transmission over fading channels. IEEE Journal on Selected Areas in Communications Volume 16, Issue 8, Oct. 1998 [33] D.J. Love, R.W. Heath Jr., et. al. What is the value of limited feedback for MIMO channels? IEEE Communications Magazine Volume 42, Issue 10, Oct. 2004 [34] Boon Poh Ng and Meng Hwa Er. Basic Array Theory and Pattern Synthesis Techniques, Chapter 16 in Handbook of Antennas in Wireless Communications. Boca Raton, FL. CRC Press. August 2001.