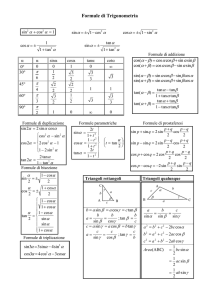
sin π 6 = 1 2 , cos π 6 = / 3 2 , sin π 3 = / 3 2 , cos π 3 = 1 2 , sin π 4
Anuncio

√ π 3 cos = , 6 2 π 1 sin = , 6 2 sin(−x) = − sin x cos(−x) = cos x tan(−x) = − tan x √ π 3 sin = , 3 2 √ π π 2 sin = cos = 4 4 2 π 1 cos = , 3 2 sin(π − x) = sin x cos(π − x) = − cos x tan(π − x) = − tan x sin(π + x) = − sin x cos(π + x) = − cos x tan(π + x) = tan x sin(x + 2kπ) = sin x cos(x + 2kπ) = cos x tan(x + kπ) = sin x π sin(x) = cos( 2 − x) π sin( 2 + x) = cos(x) cos( π2 + x) = − sin(x) ∀k ∈ N sin2 x + cos2 x = 1 p tan x sin x = ± 1 − cos2 x = ± √ , 1 + tan2 x p cos x = ± 1 − sin2 x = ± √ 1 1 + tan2 x Formule di addizione e sottrazione sin(x + y) = sin x cos y + sin y cos x sin(x − y) = sin x cos y − sin y cos x cos(x + y) = cos x cos y − sin y sin x cos(x − y) = cos x cos y + sin y sin x tan x+tan y tan x−tan y tan(x + y) = 1−tan x tan y tan(x − y) = 1+tan x tan y Formule di duplicazione sin(2x) = 2 sin x cos y cos(2x) = cos2 x − sin2 x = 1 − 2 sin2 x = 2 cos2 x − 1 2 tan x tan(2x) = 1−tan 2x Formule di bisezione q x sin( x2 ) = ± 1−cos q 2 x cos( x2 ) = ± 1+cos q 2 tan( x ) = ± 1−cos x 2 sin x = 2 tan x2 1 + tan2 x2 cos x = 1+cos x 1 − tan2 1 + tan2 x 2 x 2 tan x = Formule di prostaferesi x−y sin x + sin y = 2 sin x+y 2 cos 2 sin x − sin y = 2 sin x−y cos x+y 2 2 x+y x−y cos x + cos y = 2 cos cos 2 2 x−y cos x − cos y = −2 sin x+y sin 2 2 1 2 tan x2 1 − tan2 x2