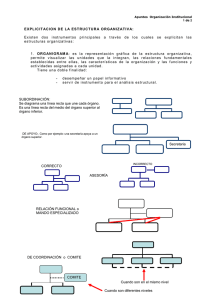
s Resto s%4 s Cociente ent(s/4)
Anuncio

La plantilla en una sola instrucción. La recursividad en Descartes es muy importante para evitar un trabajo excesivo. La opción anterior es una forma de lograrlo, pues solo se necesitan cuatro instrucciones, en lugar de las 16 de la primera opción. No obstante, existen otros atajos que sólo requiere de un poco de lógica y el uso de conceptos básicos de la aritmética. Veamos, para obtener los 16 cuadros, podemos usar una familia con un intervalo [0, 15]. El reto es cómo lograr las coordenadas de los vértices de cada cuadro: Observemos que cada hilera tiene un grupo de abscisas que varían de 0 a 3. Si usamos la expresión s%4, obtenemos el residuo o resto de la división de s con 4, que presentamos en el siguiente cuadro (% es el operador de JavaScript que genera el resto). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Resto 0 s%4 1 2 3 0 1 2 3 0 1 2 s 3 0 1 2 3 Logrando que se generen las abscisas requeridas para nuestra plantilla. Por otra parte, necesitamos que las ordenadas vayan de 0 a 3 por cada grupo de cuatro abscisas. Si usamos la expresión ent(s/4), obtenemos el cociente de la división de s con 4, que presentamos en el siguiente cuadro (ent() es una función matemática que devuelve la parte entera de la división): s 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Cociente 0 ent(s/4) 0 0 0 1 1 1 1 2 2 2 2 3 3 3 3 Si comparamos los dos cuadros, observamos que se generan las cuatro hileras con las coordenadas correspondientes. Ahora, sólo nos resta sumar estas expresiones a nuestro polígono original: (0,0)(0,1)(1,1)(1,0)(0,0), obteniendo: (s%4,ent(s/4))(s%4,ent(s/4)+1)((s%4)+1,ent(s/4)+1)((s%4)+1,ent(s/4))(s%4,ent(s/4)) Y, además, ajustar el intervalo y pasos de la familia. 80