Dominios Funciones
Anuncio

I.E.S. “ÉLAIOS” - DEPTO.MATEMÁTICAS
MATEMÁTICAS APLICADAS A CC. SOCIALES II
TEMA: ANÁLISIS DE FUNCIONES
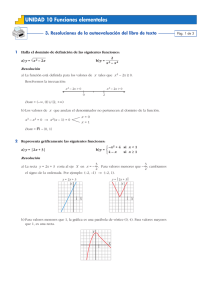
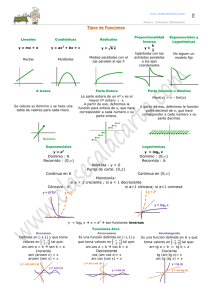
Dominio de funciones.Funciones polinómicas: su dominio siempre es R
Ejemplo: f(x) = x3 – 2x2 + 6x - 5 Dom f = R
x
x
Funciones exponenciales: y = a y = (1/a)
en ambos casos Dom f = R
( a > 1, 0 < 1/a < 1)
Funciones logarítmicas: y = loga x y = log1/a x en ambos casos Dom f = R+
( a > 1, 0 < 1/a < 1)
Funciones racionales: su dominio son todos los números reales excepto los que son raíces del
denominador.
3
2
Ejemplo: f(x) = (3x – 5) / (x – 1) Dom f = R – {-1 , 1}
Funciones irracionales: se deben excluir de su dominio aquellos valores de x para los cuales sean
negativas las expresiones que aparezcan bajo raíces de índice par.
Ejemplo: f(x) =
x + 3 Dom f = [-3 , ∞)
Funciones compuestas: los anteriores tipos de funciones se combinan. Para calcular su dominio se
deben tener en cuenta las condiciones que impone cada un a de ellas.
Ejemplo: f(x) = log( x + 2)
Para que exista el logaritmo, x + 2 > 0, x > - 2
Para que exista la raíz, log (x + 2) ≥ 0, x + 2 ≥ 1, x ≥ - 1
Ambas condiciones se resumen en que x ≥ - 1
Luego Dom f = [-1 , ∞)
Ejercicios.- Calcula el dominio de cada una de las siguientes funciones:
a)
f ( x) = log(3 x + 5)
3x + 1
x −1
g)
f ( x) =
h)
f ( x) = 3
i)
f ( x) = e
f ( x) = log( x 2 − 2 x − 3)
x 2 − 5x + 6
x 2 − 7 x + 12
b)
f ( x) =
c)
f ( x) = x − 25
d)
f ( x) = log
e)
f ( x) =
3x − 5
x−2
j)
f)
f ( x) =
12 x 3
2x + 5
k) f ( x) = log
2
Soluciones:
( x + 1)·( x + 2)
x+3
1
x
x+6
7x
x −5
a) (-5/3 , +∞); b) R – {3 , 4}; c) (-∞ , -5] U [5 , +∞); d) (-3 , -2) U (-1 , +∞);
e) (-∞ , 5/3] U (2 , +∞); f) (-5/2 , +∞); g) [-1/3 , 1) U (1 , +∞); h) R – {0};
i) [-6 , +∞); j) (-∞ , -1) U (3 , +∞); k) (-∞ , 0) U (5 , +∞).