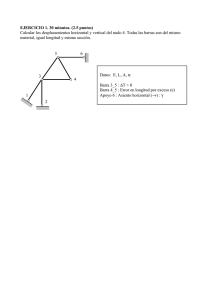
0-5Metodo de las fuerzas

Método de las Fuerzas
1. Generalidades
El método de las fuerzas se utiliza para resolver estructuras hiperestáticas. Consiste
en “liberar” una cantidad de vínculos (pueden ser externos o internos de la estructura)
hasta llegar a una estructura isostática. El número de vínculos eliminados será igual al
grado de hiperestaticidad de la estructura 1.
Para reproducir el problema original en esta “nueva” estructura aparecen como
fuerzas externas, además de las cargas que están aplicadas sobre la estructura, las
reacciones o fuerzas internas provocadas por los vínculos liberados.
Estas fuerzas que sustituyen a los vínculos liberados constituyen incógnitas que es
necesario determinar.
A la nueva estructura se le imponen las condiciones en desplazamientos que son
compatibles con los vínculos liberados. De esa manera se reproduce el problema
original y se obtienen ecuaciones que permiten calcular las incógnitas.
En definitiva para resolver la estructura hiperestática original se analiza una
estructura isostática, con ciertas fuerzas como incógnitas (X1, X2.... Xn) donde el numero
de incógnitas n es igual al grado de hiperestaticidad de la estructura.
Podemos distinguir dos tipos de fuerzas incógnitas:
A) Cuando las incógnitas sustituyen vínculos externos. Por ejemplo, al eliminar un
apoyo la fuerza de éste es sustituida por una fuerza incógnita. En este caso
impondremos la condición de que el apoyo no se desplaza.
B) Cuando se trata de un vínculo interno de la estructura. Por ejemplo, al cortar la
estructura para convertirla en isóstática se estará eliminando una (o más de una)
solicitación en ese punto. En una estructura plana de vigas sometida a cargas planas la
solicitación eliminada puede ser el momento flector, el cortante o la directa. Si la
estructura o las cargas son espaciales (o ambas lo son) la solicitación podrá ser, además
de las anteriores, el cortante y el momento flector en el otro plano y el momento torsor.
1
A veces, cuando se aplican condiciones de simetría o anti-simetría, puede llegarse a una estructura que
en primera instancia parece ser un mecanismo (no hay equilibrio). En esos casos, pueden agregarse
vínculos que sean compatibles con los desplazamientos esperados, hasta llegar a una estructura isostática.
Este asunto será visto en forma detallada mas adelante.
En este caso la incógnita hiperestática que deberá tomarse es la magnitud de la
solicitación eliminada. En su lugar deberá colocarse una fuerza aplicada de un lado del
corte realizado y otra fuerza contraria a la anterior aplicada del otro lado del corte.
La condición en desplazamientos que impondremos en este caso es que se mantenga la
continuidad de la viga, o sea que en el punto donde se realizó el corte, ambos extremos
tengan los mismos desplazamientos y giros.
Para una mejor presentación del tema en una primera instancia consideraremos
solo la existencia de vínculos del tipo A). Más adelante veremos los del tipo B).
Tampoco estaremos considerando en esta primer etapa los cambios de temperatura de
la estructura.
Aceptaremos además que la estructura que estamos analizando (que la
llamaremos estructura original hiperestática) es una estructura estable, compuesta por
un material elástico-lineal, y que la estructura isostática que resulta de eliminar los
vínculos es también una estructura estable.
En la estructura isostática obtenida (que llamaremos estructura fundamental) los
desplazamientos en los apoyos pueden ser expresados como la suma de los
desplazamientos producidos (en la estructura fundamental) por las mismas cargas
aplicadas sobre la estructura hiperestática, más los desplazamientos producidos por las
fuerzas incógnitas.
El desplazamiento ( δi ) del punto donde se encuentra aplicada la fuerza Xi , en
su misma dirección, puede representarse de la forma:
δ i = δ i 0 + δ i1 X 1 + ... + δ in X n
Donde δi0 es el desplazamiento del punto i (de la estructura fundamental)
producido por el mismo estado de cargas que hay aplicado sobre la estructura original.
A este estado de cargas le llamaremos Estado 0.
Los restantes coeficientes δij son el desplazamiento en el punto de aplicación de
la fuerza Xi y en la dirección de la fuerza Xi, producido por una carga unitaria Xj =1. Al
estado que consiste en la fuerza unitaria Xj aplicada en la estructura fundamental lo
llamaremos estado j.
El conjunto de estos coeficientes pueden ser ordenados en forma matricial y no
son otra cosa que la matriz de flexibilidad de la estructura fundamental tomando como
fuerzas aplicadas las fuerzas X. A esta matriz la denominaremos (F)XX.
Debe observarse cuando δi es un desplazamiento que los coeficientes δi0 tienen
dimensión de longitud, mientras que los coeficientes δij tienen dimensión de
longitud/fuerza si la incógnita correspondiente es una fuerza o de 1/fuerza si la
incógnita correspondiente es un momento. En cambio si δi es un giro medido en
radianes los coeficientes δi0 tienen dimensión de radianes, mientras que los coeficientes
δij tienen dimensión de radianes/fuerza si la incógnita correspondiente es una fuerza o
de radianes/(longitud*fuerza) si la incógnita correspondiente es un momento.
2
2. Ecuaciones canónicas
La condición del desplazamiento para el punto de aplicación de Xi que debemos
imponer es que:
δi = 0
Debiendo cumplirse en definitiva que:
δ i 0 + δ i1 X 1 + ... + δ in X n = 0
(1)
Teniendo en cuenta que debemos imponer la misma condición para i desde 1 a n,
tendremos n ecuaciones que podemos representar matricialmente como:
r
r
δ 0 + ( F ) XX X = 0
(2)
r
Donde δ 0 es el vector de dimensión n que expresa los desplazamientos (en la estructura
fundamental) en los puntos de aplicación de las cargas X, producidos por las cargas
aplicadas sobre la estructura original.
De esta manera se obtiene un sistema de n ecuaciones con n incógnitas (vector
X). Debe observarse que si la estructura fundamental es estable, como habíamos
supuesto, entonces la matriz (F)XX no es singular y el sistema siempre tendrá una y una
sola solución. Con los valores de X conocidos podemos hallar todos los diagramas de
solicitación.
Estas ecuaciones son denominadas usualmente Ecuaciones Canónicas del
método de las fuerzas.
Si hubiéramos despejado X se tendría que:
r
1 r
X = −( F ) −XX
δ0
3. Principales definiciones empleadas
Resumiendo los conceptos fundamentales anteriormente planteados se puede decir
que:
“Sistema Hiperestático Original” será la estructura original que queremos resolver.
Sistema Fundamental (o “Estructura Isostatizada”) será la estructura que es el resultado
(tomando la estructura original como base) de quitarle una cierta cantidad de vínculos
hasta obtener una estructura estable e isostática.
3
Estado 0 será el análisis que realizamos cuando se considera la Estructura Fundamental
cargada con todas las fuerzas externas (o sea con el sistema de cargas que tiene el
Sistema Hiperestático Original).
Estado j (con j entre 1 y n) será el análisis cuando se considera la Estructura
Fundamental con la carga unitaria Xj =1.
Sistema equivalente será la superposición del estado 0 con los estados 1 a n
(multiplicados por los valores de Xj hallados), de manera que los desplazamientos en los
apoyos sean todos cero. En este sistema se obtienen las mismas solicitaciones que en el
sistema hiperestático original.
4. Formulación matricial
Se puede hacer el mismo análisis empleando una notación matricial.
Consideremos la estructura fundamental cargada con todas las fuerzas externas
presentes y con las fuerzas incógnitas y denominemos:
P al vector de las fuerzas aplicadas sobre la estructura original
∆ P al vector de desplazamientos asociado a las fuerzas que componen el vector P
X al vector de fuerzas incógnita, que resultan de sustituir los apoyos eliminados
∆ X al vector de desplazamientos asociado a las fuerzas X
Teniendo en cuenta que la estructura fundamental es isostática y estable, tendrá
una matriz de flexibilidad no singular. Esta matriz la podemos construir tomando
primero las fuerzas P y luego las incógnitas X y del mismo modo primero los
desplazamientos ∆ P y luego los desplazamientos ∆ X . De esa manera la matriz de
flexibilidad puede ser subdividida en cuatro submatrices: FPP que relaciona los
desplazamientos ∆ P con las fuerzas P, FPX que relaciona los desplazamientos ∆ P con
las fuerzas X, FXP que relaciona los desplazamientos ∆ X con las fuerzas P, y FXX que
relaciona los desplazamientos ∆ X con las fuerzas X. Esta relación la podemos expresar
como:
 ∆P

∆X
F
Donde la matriz  PP
 FXP
FPX
FXX
  FPP
 = 
  FXP
FPX
FXX
 P 
 
 X 

 es la Matriz de Flexibilidad del Sistema Fundamental.

Entonces tenemos que:
∆ P = FPP P + FPX X
∆ X = F XP P + F XX X
r
Obsérvese que el término FXP P no es otra cosa que el vector
utilizado anteriormente.
δ0
que habíamos
4
Como los apoyos no se desplazan sabemos que el vector ∆ X = 0 , entonces:
F XP P + F XX X = 0
Como FXX es cuadrada y no singular, será invertible y en consecuencia podemos
despejar X, obteniendo:
−1
X = −FXX
FXP P
Por otro lado sustituyendo en la otra igualdad tenemos que:
−1
∆ P = FPP P + FPX X = FPP P + FPX ( −FXX
FXP P ) ⇒
−1
∆ P = (FPP − FPX FXX
FXP ) P
−1
La matriz (FPP − FPX FXX
FXP ) que se obtiene a partir de la matriz de flexibilidad
de la estructura fundamental relaciona los desplazamientos ∆ P con las fuerzas P,
debiendo observarse que han sido eliminados de esta expresión los términos con X.
O sea que, expresado de otra manera, es la Matriz de Flexibilidad de la
estructura hiperestática original.
Esta es la forma en que se relacionan la matriz de flexibilidad de la estructura
fundamental con la de la estructura hiperestática original.
5. Utilización de Castigliano
Hallar la matriz de flexibilidad de la estructura fundamental calculando directamente
los desplazamientos puede en muchos casos ser un problema complicado. Es por eso
que es más común utilizar para ello el segundo Teorema de Castigliano.
es la componente i del vector ∆ X , o sea el
desplazamiento correspondiente a la fuerza Xi, se debe cumplir (en virtud que los apoyos
no se desplazan), para todo i tal que 1≤ i ≤ n, que:
Para ello usamos que si
∆Xi
∂U
= ∆ Xi = 0
∂X i
Esto presupone poder colocar la energía de deformación de la estructura en función
de las fuerzas P y X. Veremos que esto es claramente más sencillo que calcular todos
los desplazamientos.
5
6. Energía de deformación de una estructura de barras
Supondremos una estructura de barras compuesta por m barras. En primera instancia
supondremos que la estructura solo esta sometida a esfuerzos de Directa y Flexión. De
acuerdo a los resultados obtenidos anteriormente se tiene que la energía de deformación
de la estructura será la suma de la energía de deformación de sus m barras. O sea:
L
2
1 m k  N 2 M x2 M y 
+
+
U = ∑U k = ∑ ∫
dz


2
EA
EI
EI
k =1
k =1 0 
x
y 
m
En consecuencia:
∂U 1 ∂
=
∂X i 2 ∂X i
2
 N k2
M yk2
M
xk

+
+
∑
∫

E
A
E
I
Ek I yk
k =1 0  k k
k xk
m Lk

dz = 0


Pero como Lk no depende de Xi tendremos que:
L
∂U 1 m k ∂
= ∑
∂X i 2 k =1 ∫0 ∂X i
2
 N k2
M yk2 
M
xk

dz
+
+
 E A EI

EI
xk
yk 
 k k
Derivando y teniendo en cuenta que Ek Ik y Ak no dependen de Xi :
L
∂U 1 m k  2 N k ∂N k 2 M xk ∂M xk 2M yk ∂M yk 
= ∑
+
+
dz
∂X i 2 k =1 ∫0  Ek Ak ∂X i Ek I xk ∂X i
Ek Iy ∂X i 
Y simplificando se tiene que:
m Lk 
N ∂N k M xk ∂M xk M yk ∂M yk 
∂U
= ∑ ∫ k
+
+
dz = 0
∂X i k =1 0  Ek A k ∂X i Ek I xk ∂X i Ek I yk ∂X i 
(3)
En el caso de un pórtico plano donde solo se tiene momento en una dirección no
aparece el termino en My, y en el caso de un reticulado, dado que no hay momentos
flectores, la expresión se reduce al primer término.
6
7. Aplicación a reticulados hiperestáticos
En el caso de un reticulado se tiene que solo hay fuerzas de directa en las barras y
que la directa es constante a lo largo de toda la barra (no depende de z), debido a que las
cargas están aplicadas en los nodos. En ese caso será:
m Lk  N
∂N k 
∂U
dz = 0
= ∑ ∫  k
∂X i k =1 0  E k A k ∂X i 
Y como la directa es constante a lo largo de la barra será:
m N
∂N k
∂U
= ∑ k
Lk = 0
∂X i k =1 Ek A k ∂X i
La directa Nk la podemos expresar superponiendo el estado 0 con los estados 1 a
n de una forma lineal en las incógnitas X:
N k = N ok + X 1 n1k + X 2 n 2 k + .......... .... + X n n nk
(4)
Donde N0k es la directa producida en la barra k de la estructura fundamental cuando
actúan las mismas fuerzas que están aplicadas sobre la estructura hiperestática original
(Estado 0), y njk es la directa que se genera en la barra k de la estructura fundamental
cuando se aplica una fuerza unitaria Xj =1.
Derivando Nk en relación a una fuerza genérica Xi se obtiene que:
∂N k
= nik
∂X i
En consecuencia la condición que debe verificarse es:
m N n L
∂U
= ∑ k ik k = 0
∂X i k =1 E k Ak
Y sustituyendo Nk por la expresión desarrollada se tiene que:
m
m
m
m
∂U
N n L
n n L
n n L
n n L
= ∑ 0 k ik k + X 1 ∑ 1k ik k + X 2 ∑ 2 k ik k .... + X n ∑ nk ik k = 0 (5)
∂X i k =1 E k Ak
E k Ak
E k Ak
k =1 E k Ak
k =1
k =1
Para i variando entre 1 y n se obtiene un conjunto de n ecuaciones con las n
incógnitas X. El sistema de ecuaciones es lineal en las incógnitas X y no es otra cosa que
las ecuaciones canónicas calculada a partir de la energía de deformación usando el
segundo Teorema de Castigliano.
El primer término es el desplazamiento en la dirección de Xi producido en la
estructura fundamental por las cargas aplicadas sobre la estructura hiperestática original.
7
El segundo es la componente de dicho desplazamiento producido por la fuerza X1 y así
sucesivamente.
O sea que los coeficientes de las ecuaciones canónicas:
r
r
δ 0 + ( F ) XX X = 0
se pueden calcular con las expresiones:
N 0 k nik Lk
(6)
k =1 E k Ak
m n jk nik Lk
(7)
δ ij = ∑
k =1 E k Ak
m
δ i0 = ∑
y
Ésta resulta ser una forma muy utilizada para resolver este tipo de problema. Se
requiere resolver la estructura fundamental (que es isostática y estable) para n+1
estados de carga.
El primer estado de cargas (estado 0) es el producido por las fuerzas aplicadas
sobre la estructura hiperestática original. Los siguientes estados de carga corresponden a
cargas unitarias aplicadas en la dirección de X1, X2,.....y Xn .
Luego con esos n+1 estados de carga resueltos para la estructura fundamental se
construyen las n ecuaciones y se calculan las fuerzas incógnitas.
8. Cuando las fuerzas incógnitas son solicitaciones internas
Veremos un teorema que permite encarar este caso de manera muy similar al caso
que las incógnitas son reacciones.
Enunciado:
Si cortamos una barra y sustituimos el vínculo por dos fuerzas de igual módulo y de
sentido contrario aplicadas en los extremos que resultan del corte, tendremos una
incógnita (que llamaremos X). Entonces la condición que debe cumplir la energía de
deformación es la misma que si el vínculo fuera externo a la estructura, o sea:
∂U
=0
∂X
Para realizar la demostración tomaremos que la solicitación de la barra es una
fuerza directa. Es fácil ver que se puede generalizar esta demostración a las otras
solicitaciones.
8
Supongamos que tenemos la barra que hemos cortado:
x
P
P
1
x
2
Sea P el punto de la barra en donde se realiza el corte y en principio admitiremos
que en ese punto están aplicadas dos fuerzas no necesariamente iguales que llamaremos
X1 y X2.
La energía de deformación que llamaremos ( U ∗ ), será una función de P, X1 y X2
que podemos expresar como U ∗ = U ∗ ( P, X 1 , X 2 )
Entonces, aplicando el 2do Teorema de Castigliano, podemos calcular el
desplazamiento de P en cada uno de los lados del corte realizado:
∂1 =
∂U ∗
(P , X 1 , X 2 )
∂X 1
∂2 =
∂U ∗
( P, X 1 , X 2 )
∂X 2
Por continuidad de la barra, se debe cumplir que ∂ 1 + ∂ 2 = 0 . Por equilibrio de
fuerzas se debe cumplir que las dos fuerzas son del mismo módulo y sentido contrario.
Luego tomamos que: X 1 = X 2 = X .
Entonces podemos notar que U ∗ ( P, X 1 , X 2 ) = U ∗ ( P, X , X ) = U ( P, X ) .
Derivando esta expresión, tenemos:
∂U
∂U ∗
∂U ∗
(
(P, X , X ) = ∂ 1 + ∂ 2 = 0 ⇒
( P, X ) =
P, X , X ) +
∂X
∂X 1
∂X 2
∂U
( P, X ) = 0
∂X
Luego podemos concluir que cuando el vínculo es interno, colocamos dos
fuerzas iguales y de sentido contrario, calculamos las solicitaciones en la estructura
fundamental y luego aplicamos la misma condición que en el caso de un vínculo
externo a la estructura.
9
9. Ejemplos de reticulados hiperestáticos
Ejemplo 1
Veremos a continuación un ejemplo con solo un grado de hiperestaticidad (n=1).
El mismo es interno. En este caso se tienen 6 barras, o sea que m = 6.
La energía de deformación será:
1 6 N i2 Li (8)
U= ∑
2 i =1 Ei Ai
Además:
N i = N i 0 + Xni
(9)
Donde N i 0 es la directa en la barra i en el Estado 0, y ni es la directa en la barra i en el
Estado 1.
Denominaremos X a la fuerza incógnita; dado que hay una sola incógnita no es
necesario utilizar subíndice.
Entonces, sustituyendo se tiene que:
U=
1 6 ( N i 0 + Xni ) 2 Li
∑
2 i =1
Ei Ai
10
∂U
= 0 (por el segundo teorema de Castigliano y
∂X
el teorema recientemente demostrado), entonces:
Sabiendo que se cumple que
6 n2L
∂U 6 ( N i 0 + Xni ) ni Li 6 N i 0 ni Li
=∑
=∑
+ X ∑ i i =0⇒
∂X i =1
Ei Ai
i =1 Ei Ai
i =1 Ei Ai
6
N i 0 ni Li
i =1 Ei Ai
∑
X =−
(10)
ni2 Li
∑
i =1 Ei Ai
6
Luego, analizando cada estado por separado, podemos calcular la directa en cada
barra, y como conocemos la geometría y el material de las mismas, podemos hallar X
(de la ecuación anterior).
Conociendo X, hallamos la directa de cada barra en la estructura original (con la
ecuación 10).
Se sugiere la siguiente Tabla para calcular X de manera ordenada:
Barra
1 (AB)
2 (BC)
3 (CD)
4 (AD)
5 (AC)
6 (BD)
Li/(EiAi)
Ni0(Estado 0) ni(Estado 1 ) Ni0*ni*Li/(EiAi)
ni2*Li/(EiAi)
Ni=Ni0+Xni
Σ
La columna “Barra” se llena con los nombres de las barras, por ejemplo: “AB”,
“BC”, etc.
En la segunda columna, se ingresan los datos de geometría y material de cada
barra. Si estamos trabajando con una estructura del mismo material, y cuyas barras
tienen la misma sección de área A, entonces los valores de E y A son independientes de
las barras y pueden ser sacados de factor común, afuera de la sumatoria. Aparecen
dividiendo al numerador y también al denominador y se simplifican. En definitiva, si E
y A no dependen de las barras (para el cálculo de la incógnita X) pueden ser eliminados
y esta columna puede ser llenada simplemente con el valor Li.
En la tercera y cuarta columna se ingresan las directas de los estados 0 y 1
respectivamente, que deben ser calculadas por alguno de los procedimientos que se
utilizan para estructuras isostáticas.
11
En la quinta y sexta columna se realizan las operaciones indicadas; o sea, para la
quinta columna se calcula el producto de la segunda por la tercera por la cuarta y para la
sexta columna el producto de la segunda por la cuarta al cuadrado.
Si estamos trabajando con una estructura del mismo material (E constante), y
cuyas barras tienen la misma sección de área A, entonces estas columnas pueden ser
llenadas sin dividir por EiAi (siendo coherente con lo realizado para calcular los valores
en la segunda columna).
En las casillas de color gris, se calculan la sumatoria de todos los valores en sus
respetivas columnas, es decir, se calculan los términos:
6
N nL
∑ i0 i i
i =1 Ei Ai
y
ni2 Li
∑
i =1Ei Ai
6
Con estos términos se halla X, y luego se calcula la última columna Ni (que es la
directa en cada barra de la estructura original).
Ejemplo 2
Veremos a continuación un ejemplo con dos grados de hiperestaticidad (n=2),
uno producido por vínculos externos y otro por vínculos internos. En este caso se tienen
10 barras, o sea que m =10. Supondremos que todas las barras son del mismo material y
que tienen la misma sección.
Realizamos el mismo razonamiento que en el ejemplo 1. En este caso tendremos
3 estados de análisis: El Estado 0, el Estado 1 y el Estado 2. La directa en cada barra
vale:
N i = N i 0 + Xni1 + Yni 2
Por comodidad utilizaremos X en lugar de X1 e Y en lugar de X2; n será la
i1
directa producida en la barra i por una fuerza X=1 y ni 2 la directa de la barra i para una
fuerza Y=1.
12
Sustituyendo la expresión de Ni en la ecuación (4) y tomando la cantidad de
barras que corresponden a este caso (m = 10) se tiene que:
1 10 ( N i 0 + Xni1 + Yni 2 ) 2 Li
U= ∑
Ei Ai
2 i =1
Luego si calculamos y anulamos las dos derivadas: ∂U = 0 y ∂U = 0
∂X
∂Y
Entonces,
10 ( N
0= ∑
i0
i =1
10 ( N
0= ∑
i0
i =1
+ Xni1 + Yni 2 )ni1 Li
Ei Ai
+ Xni1 + Yni 2 )ni 2 Li
Ei Ai
Entonces tendremos que:
10 n 2 L
i1 i
X∑
i =1 Ei Ai
10 n ni 2 Li
i1
X∑
i =1
10 n n L
i1 i 2 i
+Y ∑
Ei Ai
i =1
Ei Ai
10 n 2 L
i2 i
+Y ∑
i =1 Ei Ai
10
N i 0 ni1 Li
i =1 Ei Ai
= −∑
(11)
10
N i 0 ni 2 Li
i =1 Ei Ai
= −∑
Este es un sistema de dos ecuaciones y dos incógnitas que podemos resolver.
Luego de hallar X e Y, podemos calcular la directa en cada barra y las reacciones,
resolviendo la estructura.
A continuación resolvemos el ejemplo.
Comenzamos colocando las longitudes de las barras en la segunda columna. No
incluimos el área y el módulo de elasticidad pues son iguales en todas las barras.
Analizaremos por separado el Estado 0: por equilibrio de nudos (o por método de
Cremona) calculamos las directas ( N i 0 ) y las colocamos en el cuadro siguiente
(columna tercera) en todas las barras.
Análogamente, analizamos el Estado 1 y Estado 2, obteniendo respectivamente las
directas ni1 y ni 2 y las colocamos en las columnas cuarta y quinta.
Luego, para cada barra calculamos los productos: ni21 Li , ni22 Li , N i 0 ni1 Li , N i 0 ni 2 Li , y
ni1 ni 2 Li (ver columnas de la 6ª a la 10ª del cuadro siguiente)
Sumando estos valores obtenemos los coeficientes del sistema de ecuaciones
(expresiones 11):
13
10 2
∑ ni1 Li
i =1
10
= 3L
∑ ni1ni 2 Li = −
i =1
10
10
i =1
i =1
∑ N i 0 ni1 Li = 3PL
10
∑ ni1ni 2 Li = −
i =1
N i0
2
L
2
∑ N i 0 ni 2 Li = − PL 2
2
L
2
ni1
ni 2
ni21 Li
ni22 Li
N i 0 ni1 Li
N i 0 ni 2 Li
ni1 ni 2 Li
Luego, aplicando las ecuaciones 11 , llegamos al siguiente sistema de ecuaciones:
3PL + 3LX −
− 2PL −
2
LY = 0
2
2
LX + 2 L(1 + 2 )Y = 0
2
Resolviendo este sistema se obtiene:
X = −P
10 + 12 2
11 + 12 2
y
Y =P
3 2
11 + 12 2
Con estos valores de X e Y calculamos la columna 11 que tiene las directas en el
reticulado hiperestático original con la expresión:
N i = N i 0 + Xni1 + Yni 2
14
Ni
Las reacciones las calculamos de manera análoga sumando los distintos estados.
También las podemos calcular de otro modo, haciendo equilibrio en esos nudos donde
están los vínculos, colocando las directas N i ya conocidas.
15
10.
Variación de temperatura
Cuando tenemos una estructura que presenta cambios de temperatura se producen
deformaciones de la estructura y en el caso de las estructuras hiperestáticas también se
producen solicitaciones.
Si tenemos la barra i (con vínculos isostáticos que le permiten deformarse libremente)
sometida a un gradiente de temperatura ∆Ti, sabemos que la deformación producida es:
ε i = α i ∆Ti
Donde α i es el coeficiente de dilatación térmica de la barra i
El estiramiento δi de la barra i será entonces:
δ i = ε i Li = α i ∆Ti Li
La estructura fundamental por ser isostática permite que se produzcan libremente las
deformaciones causadas por la variación térmica de las barras. En esta deformación
libre solo se producen estiramientos o retracciones de las barras y no se producen
tensiones o solicitaciones en la estructura.
Para resolver la estructura podemos suponer este efecto como un estado de
desplazamientos más de la estructura que llamaremos Estado T .
En este caso someteremos a la estructura fundamental a los desplazamientos producidos
por las cargas (Estado 0) y a continuación a las deformaciones producidas por la
temperatura.
Las fuerzas incógnitas X tendrán que ser tales que su efecto sumado con las dos
anteriores (Estado 0 y Estado T) anulan los desplazamientos en los apoyos.
En este caso la ecuación canónica la podemos expresar agregándole el termino de la
temperatura, quedando:
r
r
r
δ 0 + δ T + ( F ) XX X = 0
11.
(12)
Descensos impuestos de los apoyos
Hasta ahora hemos supuesto que los apoyos no tienen desplazamientos. Puede suceder
que se produzcan movimientos de los apoyos como habíamos visto en el caso de las
vigas continuas. En este caso el desplazamiento no es igual a cero sino que es un valor
conocido.
Estos desplazamientos pueden aparecer solo en los puntos de aplicación de las fuerzas
incógnitas externas a la estructura.
16
En las incógnitas que surgen de realizar cortes en las barras (donde se aplica la
condición de continuidad de la barra) no tiene sentido que aparezcan pues se estaría
rompiendo o quebrando la barra en ese punto.
Podemos incorporar un vector de los desplazamientos impuestos δDI que puede tener
algunos componentes diferentes de cero y otros nulos.
Las ecuaciones canónicas (considerando también el efecto de la variación de
temperatura) quedan en este caso:
r
r
r
δ 0 + δ T + ( F ) XX X = δ DI
12.
(13)
Aplicación a una viga isostática
Si bien el objeto de este capítulo es estudiar las estructuras hiperestáticas se introduce
este ejemplo de aplicación de Castigliano para facilitar la comprensión del método y de
la utilización de las integrales de Mohr.
Debe hacerse notar que Castigliano puede ser aplicado tanto a estructuras hiperestáticas
como isostáticas.
Sea entonces una ménsula AB.
P
A
B
C
L/2
L/2
L
z
Conocemos el diagrama de momentos:
M = M ( z) = − P z
La energía de deformación será:
1 LM 2
P2 L 2 1 P2 z3
U= ∫
dz =
∫ z dz
2 0 EI
2 EI 0
2 EI 3
L
=
0
P 2 L3
6 EI
Para obtener la flecha en el extremo B tenemos que derivar la energía de deformación
respecto de la fuerza P.
17
Aplicando el 2do Teorema de Castigliano
∆B =
∂U
PL3
⇒ ∆B =
∂P
3EI
Resultado que obviamente coincide con el que se obtenía con otros métodos.
Calculemos ahora la flecha en el punto medio C. Para eso colocamos en C una fuerza
ficticia Q con dirección vertical y sentido hacia abajo (ver figura).
Luego calculamos el diagrama de momentos y luego la energía de deformación en
función de Q. Obsérvese que si bien Q no es estrictamente una incógnita hiperestática X,
se puede en la practica trabajar como si lo fuera.
Luego derivamos respecto a Q, e igualamos Q=0
Tendremos que:
M = M 0 + Qm1
U=
1 LM 2
1 L (M 0 + Qm1 )2
dz
=
dz ⇒
∫
∫
2 0 EI
20
EI
∆C =
L m2
∂U L M 0 m1
=∫
dz + Q ∫ 1 dz
∂Q 0 EI
0 EI
De las tablas de Integrales de Mohr:
L
∫
0
M 0 m1
1 L (L 2) 
PL 
5
dz =
PL3
 2 PL +
=
EI
EI 2 6 
2  48 EI
m12
1 LLL
L3
dz
=
=
∫0 EI
EI 2 2 3 12 EI
L
18
pero como Q=0, entonces:
L
M m
∂U
5
= ∫ 0 1 dz =
PL3 ⇒
∂X 0 EI
48 EI
∆C =
5
PL3
48 EI
Resultado que también coincide con los obtenidos con otros métodos.
Resumiendo, para calcular el desplazamiento en un punto seguimos los siguientes
pasos:
Caso 1: En B hay una fuerza externa P que tiene igual dirección que el desplazamiento
que queremos calcular.
1º. Calculamos el diagrama de momento flector en función de P.
2º. Calculamos la energía de deformación U=U(P), y luego derivamos U
respecto a P, obteniendo el desplazamiento deseado.
Caso 2: En C no existe una fuerza externa que tenga igual dirección que el
desplazamiento que queremos calcular.
1º. Creamos un nuevo estado de análisis con una fuerza Q aplicada en C, con
igual dirección que el desplazamiento que queremos calcular (en realidad, lo que
hacemos es colocar una fuerza adimensional de valor 1 y multiplicamos todo el estado
por Q).
2º. Calculamos U=U(P,Q), y luego derivamos U respecto a Q.
3º. Luego imponemos Q=0 y obtenemos el desplazamiento deseado.
13.
Aplicación a pórticos hiperestáticos
En el caso de un pórtico plano en las barras hay fuerzas de directa, de cortante y de
flexión dentro del plano de la estructura.
En este caso por razones que veremos más adelante se acepta que las energías de
deformación por cortante y directa son mucho más pequeñas que la producida por
flexión y por lo tanto pueden despreciarse frente a la energía producida por la flexión.
Existen algunos casos donde no es razonable despreciar las energías de directa y
cortante pero este asunto será visto más adelante.
Consideremos un pórtico plano compuesto de m barras y con un grado n de
hiperestaticidad. La energía de deformación será:
19
m
U = ∑U k =
k =1
1 m Lk  M 2 
dz
∑ ∫
2 k =1 0  EI 
(14)
Imponiendo la condición de desplazamientos se tendrá que:
m Lk  M
∂M k 
∂U
dz = 0
= ∑ ∫  k
∂X i k =1 0  E k I k ∂X i 
El momento flector Mk lo podemos expresar superponiendo el estado 0 con los estados 1
a n obteniendo una expresión lineal en las incógnitas X:
M k = M 0k + X 1m1k + X 2 m2 k + .............. + X n mnk
(15)
Donde M0k es el flector producido en la barra k de la estructura fundamental cuando se
aplican las fuerzas que están aplicadas sobre la estructura hiperestática original.
mjk es el momento flector que se genera en la barra k de la estructura fundamental
cuando se aplica una fuerza unitaria Xj =1.
Derivando Mk en relación a una fuerza genérica Xi se obtiene que:
∂M k
= mik
∂X i
Por lo que la condición de desplazamientos es:
m Lk  M m
∂U
= ∑ ∫  k ik
∂X i k =1 0  E k I k

dz = 0

(16)
Desarrollando Mk , se tiene para cada i entre 1 y n una ecuación de la forma:
m Lk  M m
∂U
= ∑ ∫  0k ik
∂X i k =1 0  Ek I k
m Lk  m m

dz + X 1 ∑ ∫  1k ik
k =1 0  E k I k

m Lk  m m

dz + X 2 ∑ ∫  2 k ik
k =1 0  E k I k

m Lk  m m

dz + .. X n ∑ ∫  nk ik
k =1 0  E k I k

En este caso no es posible eliminar las integrales como se hacía con la directa pues el
momento flector normalmente depende de z.
O sea que los coeficientes de las ecuaciones canónicas:
r
r
δ 0 + ( F ) XX X = 0
se tienen que calcular con las expresiones:
20

dz = 0

m Lk
M
(17)
m 
δ i 0 = ∑ ∫  0 k ik dz
k =1 0  E k I k 
y
m Lk
m m 
jk ik
dz
δ ij = ∑ ∫ 

k =1 0  E k I k 
(18)
A las integrales que sumadas proporcionan los coeficientes de la ecuación o sea:
Lk
∫
0
m jk mik
Ek I k
dz
y
Lk
M 0k m jk
0
Ek I k
∫
dz
se les denomina Integrales de Mohr.
Normalmente están tabuladas para varios tipos de diagramas de momentos. De esta
manera, para resolver los ejercicios, en general no es necesario calcular estas integrales
sino que basta con ir a la tabla correspondiente y buscar en el cuadro de doble entrada el
tipo de diagrama de Momento (ejemplo, triangular - rectangular, o rectangular –
parabólico etc).
Cabe señalar que si bien los momentos M0k producidos por las fuerzas aplicadas sobre la
estructura original pueden tener cualquier forma los que corresponden a las fuerzas
unitarias Xi = 1 tiene formas mas sencillas.
Para una estructura de barras rectas los diagramas de los estados 1 a n pueden ser
representados por tramos rectos, lo que simplifica mucho el cálculo de las integrales de
Mohr.
Conociendo los n+1 diagramas de momentos de cada barra se pueden calcular los
valores de todas las integrales de Mohr y hallar los coeficientes del sistema a de n
ecuaciones con n incógnitas.
Debe observarse que si alguna de las incógnitas proviene de haber cortado alguna barra
razonando en forma análoga al caso de directa se tendrá que la condición que debemos
imponer (tomando dos fuerzas unitarias iguales y contrarias) es la misma que para el
caso de los apoyos.
De existir descensos de apoyos o variaciones de temperatura deben colocarse los
términos correspondientes.
21
14.
Ejemplo de pórtico hiperestático
En el pórtico de la siguiente figura, se observa una estructura con 2 grados de
hiperestaticidad. Dicho pórtico, presenta un empotramiento en el punto A, y un apoyo
fijo en el punto B. Si quitamos el vínculo en B, la estructura resultante es isostática.
Sistma
Hiperestático
Original
A
B
E0
A
E1
B
A
E2
B
A
B
X1
En este caso el grado de hiperestaticidad de la estructura es 2 y en consecuencia resultan
dos incógnitas X1 y X2.
En principio se puede liberar cualquier vínculo siempre y cuando la estructura resultante
sea estable e isostática.
Elegiremos liberar el apoyo en B generando dos incógnitas que llamaremos X1 y X2. La
opción entre unos u otros se hace procurando que la resolución de los estados de carga
sea lo mas sencilla posible. El vector X lo podemos notar:
r X 
X =  1 
X2 
La derivada de la energía de deformación en relación a las incógnitas deberá ser cero
para que no haya desplazamientos de B.
Se resuelven los 3 estados de carga [E0, E1, y E2] y trazamos los diagramas de
momentos de todas las barras de la estructura para cada estado.
Con estos diagramas se calculan integrales de Mohr para cada barra y cada combinación
de estados necesaria.
Sumando las columnas se obtienen los coeficientes de la dos ecuaciones.
22
X2
Resolviendo las dos ecuaciones se obtienen X1 y X2 . Finalmente sumando los tres
estados se obtienen los diagramas de momentos en toda la estructura.
15.
Condiciones de simetría para estructuras planas
Antes de analizar las condiciones de simetría realizaremos algunas consideraciones
sobre las estructuras y las cargas planas.
Normalmente en los cursos se han estudiado hasta ahora estructuras planas. Mas allá de
la idea intuitiva que tenemos de ellas es conveniente precisar la definición de las
mismas.
Diremos que una estructura es plana si se cumple que a) todos los ejes de sus barras
pertenecen a un plano y b) este plano, al que pertenecen todos los ejes, es plano de
simetría de la estructura, o sea de todas sus barras.
Por otro lado diremos que las cargas, aplicadas sobre una estructura plana, son planas si
están compuestas por fuerzas contenidas en el plano de simetría de la estructura o por
momentos que pueden ser definidos por fuerzas ubicadas en dicho plano. Dicho de otra
manera estos serán momentos perpendiculares al plano de simetría de la estructura.
Es claro que en las condiciones de una estructura plana sometida a cargas planas las
reacciones que puedan producirse en los apoyos también serán planas, del mismo modo
que también lo serán las solicitaciones que aparecen en las barras de la estructura. En
estas condiciones se verificará también que los desplazamientos de la estructura se
producirán pero manteniendo la estructura en el plano original.
Si tomamos un sistema de ejes coordenados con los ejes x e y que pertenecen al plano
de simetría de la estructura, el eje z será perpendicular a dicho plano. De acuerdo a lo
anterior la carga será plana si todas las fuerzas y momentos aplicados son tales que las
fuerzas no tienen componente según z y los momentos aplicados no tienen componentes
según x e y.
En consecuencia las reacciones, solicitaciones de la estructura y los desplazamientos de
la misma serán tales que la componente según z de fuerzas y desplazamientos es nula y
que las componentes según x e y de momentos y giros son nulas también.
Estructura Simétrica con Cargas Simétricas (ESCS)
Diremos que una estructura plana es simétrica (en relación a un eje que pertenece al
plano) si existe simetría de su forma en relación a ese eje y si las propiedades de las
barras y los vínculos también son simétricos. Aceptaremos que tomamos el eje y de
nuestro sistema de coordenadas coincidiendo con el eje de simetría de la estructura.
Diremos que una estructura simétrica está sometida a cargas simétricas si el eje y (de
simetría de la estructura) es también eje de simetría de las cargas.
De acuerdo a lo anterior, para una estructura con el eje de simetría vertical:
Si en un punto Q perteneciente a la estructura, está aplicada una carga horizontal, en Q´
(simétrico de Q) estará aplicada una carga de igual magnitud y sentido contrario.
23
Si en Q está aplicada una carga vertical, en Q´ estará aplicada una carga de igual
magnitud y sentido.
Si en Q está aplicado un momento en Q´ estará aplicado un momento de sentido
contrario.
En la figura siguiente se muestra una estructura simétrica sometida a cargas simétricas.
Veremos este caso, que tiene características generales, en primer lugar y luego veremos
otros casos que introducen aspectos particulares de las estructuras o las cargas.
A
B
Dado cualquier pórtico cargado, que presente las condiciones de simetría mencionadas,
tendremos también condiciones de simetría de las solicitaciones y de los
desplazamientos de la estructura. En particular, en los puntos de intersección de las
barras con el eje de simetría (A y B en este caso) se puede inferir que:
Los puntos A y B no tienen desplazamiento horizontal (según el eje x) pues si lo
tuvieran hacia un lado por razones de simetría tendrían que tenerlo hacia el otro lado.
En cambio pueden tener desplazamientos verticales pues el simétrico de un
desplazamiento vertical es ese mismo desplazamiento.
Tampoco pueden tener giros pues si tuvieran un giro por razones de simetría tendrían
que tener el contrario y en consecuencia éste deberá ser nulo.
Analizadas las solicitaciones, tenemos que, si hay un cortante hacia arriba del lado
derecho del punto A, entonces, por razones de simetría, debiera haber un cortante hacia
arriba del otro lado. Pero para estar en equilibrio el cortante de un lado y otro deben
tener sentido contrario. Luego la única posibilidad es que el cortante sea nulo en A.
En cambio si hubiera un momento antihorario del lado izquierdo de A tendría que haber,
por razones de simetría, un momento horario del lado derecho. Estos dos momentos se
equilibran y son posibles. Luego el momento puede ser diferente de cero.
En relación a la directa, si del lado izquierdo tiene un sentido (por razones de simetría)
del lado derecho debe tener el sentido contrario. Ambas fuerzas se equilibran y también
es posible que sean distintas de cero.
24
Consideraciones análogas pueden hacerse para el punto B.
En consecuencia si llamamos u a los desplazamientos horizontales (según el eje x) , θ a
los giros y V al cortante se debe cumplir que:
uA = 0
uB = 0
θA = 0
θB = 0
VA = 0
VB = 0
En estas condiciones la estructura puede ser cortada por el eje de simetría y, teniendo en
cuenta que el cortante es cero en A y B, colocar en cada uno de esos puntos dos
incógnitas que serán la directa y el momento flector. La condición que debemos
imponer es que el giro y el desplazamiento horizontal de los puntos A y B sea cero. De
esa manera se obtienen las 4 condiciones que nos permiten calcular las 4 fuerzas
incógnitas
X3
X1
X4
X2
Se deberá cumplir la condición que la derivada de la energía de deformación en relación
a X1, X2 , X3 y X4 sea nula.
En definitiva tenemos un problema con la mitad de la estructura y con cuatro fuerzas
incógnitas como se indica en la figura.
Debe observarse que si no se hubieran hecho consideraciones de simetría, la estructura
tenía 6 fuerzas incógnitas. Esto hubiera implicado resolver 7 estados de solicitaciones
en toda la estructura y calcular 27 coeficientes (6 del vector y 21 de la matriz teniendo
en cuenta que la misma es simétrica).
De acuerdo a las consideraciones realizadas podemos resolver una estructura con 4
fuerzas incógnitas. Esto implica resolver 5 estados de solicitaciones en la mitad de la
estructura y calcular 14 coeficientes (4 del vector y 10 de la matriz).
25
Es evidente que usando las propiedades de simetría el problema se simplifica
considerablemente.
Es de hacer notar que las consideraciones realizadas para esta estructura se pueden
generalizar a cualquier otra. En el caso en que las barras que llegan al eje no sean
horizontales el razonamiento sería el mismo. En ese caso sería cero la fuerza vertical
que se trasmite en el punto del eje. Por estar inclinadas las barras no sería nula la directa
ni el cortante, pero tendríamos las mismas incógnitas: la fuerza horizontal y el
momento.
Veremos un segundo caso de estructuras simétricas con cargas simétricas. En este caso
tendremos el caso particular cuando una de las fuerzas está aplicada en un punto del eje
de simetría de la estructura como se indica en la siguiente figura.
P
A
B
Si suponemos que en el punto A hay una fuerza aplicada podemos concluir que por
razones de simetría debiera ser simétrica de sí misma. Esto hace que no pueda ser una
fuerza horizontal pues su simétrica sería de dirección contraria. Tampoco puede ser un
momento aplicado porque el simétrico de un momento aplicado es el momento
contrario. Solo es posible que exista una fuerza vertical pues su simétrica es ella misma.
Considerando la fuerza vertical P aplicada en A se tiene que su efecto es equivalente al
de dos fuerzas simétricas, del mismo sentido que P y de valor P/2 aplicadas en dos
puntos simétricos y tan próximos como se quiera del eje de la estructura.
Luego el problema puede ser estudiado tomando sobre la estructura cortada una fuerza
aplicada de valor P/2. Las incógnitas en este caso serán las mismas que en el caso
general anteriormente estudiado. Lo único diferente es que en el punto que pertenece al
eje de simetría se toma la mitad de la fuerza P como se observa en la figura siguiente.
26
P/2
X3
X1
X4
X2
Veremos un tercer caso de estructuras simétricas con cargas simétricas. En este caso
tendremos el caso particular que una de las barras pertenece al eje de simetría como se
indica en a figura siguiente.
A
B
barra BC
Área: A
La barra BC que pertenece al eje de simetría de la estructura, para un estado de carga
simétrico de acuerdo a lo que ya vimos en el caso 1, no tendrá desplazamientos
horizontales ni giros en ninguno de sus puntos. Esto hace que se mantenga en el eje de
simetría. Como consecuencia de ello no estará flexionada y las solicitaciones momento
y cortante serán nulas en toda su extensión. Puede, en cambio, tener desplazamientos
verticales y en consecuencia fuerza directa.
Como no tiene momento puede considerarse (sin modificar el problema) que está
articulada en sus extremos. Por otro, lado su directa estará causada por dos componentes
iguales. Una que proviene de las cargas aplicadas del lado derecho de la estructura y
otra que proviene de las cargas ubicadas del lado izquierdo.
Teniendo en cuenta que al considerar la mitad de la estructura se considera la mitad de
la directa aplicada sobre esta barra, para restaurar el problema original debemos tomar
27
en la estructura simplificada una barra que tenga la mitad del área que tienen la
estructura real como se indica en la figura.
X3
X1
X4
B
X2
barra BC: tomo A'=A/2
C
Si además despreciáramos las deformaciones por compresión en relación a las
producidas por flexión (como se hace frecuentemente) tendríamos que la barra BC no
tendría deformaciones significativas por directa (única solicitación a la que esta
sometida) y por lo tanto podríamos sustituir esta semi-barra por una fuerza vertical
incógnita X5 aplicada en B e imponer la condición que el descenso de B sea nulo (o sea
la derivada de la energía de deformación en relación a X5) en este caso tendríamos un
sistema de 5 ecuaciones con 5 incógnitas. Es de hacer notar que el problema original,
sin realizar consideraciones de simetría, hubiera tenido 9 ecuaciones y 9 incógnitas.
El cuarto caso se trata de un pórtico simétrico con cargas simétricas, que al cortarlo por
su eje, y haciendo solamente eso, llegaríamos a un mecanismo (ver siguiente figura).
A
B
28
X3
X1
X4
X2
En este caso, sabemos (por simetría) que el desplazamiento horizontal del punto A es
nulo. Por lo tanto, se puede decir que en el punto A existe un vínculo ficticio que
restringe el desplazamiento horizontal, o sea que para el análisis, podemos colocar un
apoyo deslizante sin modificar el problema original. En ese caso, llegamos a una
estructura fundamental isostática como se indica en la siguiente figura.
X3
X4
X2
En este problema aparecen solamente 3 incógnitas X mientras que la estructura original
antes de realizar consideraciones de simetría aparecían 4 incógnitas.
Estructura Simétrica con Cargas Antisimétricas (ESCAS)
Si tenemos una estructura simétrica con un eje de simetría diremos que las cargas son
antisimétricas si son tales que para todo punto Q de la estructura que este cargado con
una carga P, se cumple que en el punto simétrico Q´ se encuentra aplicada la carga
contraria a la simétrica de P.
De acuerdo a lo anterior para una estructura con el eje de simetría vertical:
Si en Q está aplicada una carga horizontal, en Q´ estará aplicada una carga de igual
sentido y magnitud.
29
Si en Q está aplicada una carga vertical, en Q´ estará aplicada una carga de igual
magnitud y sentido contrario.
Si en Q está aplicado un momento, en Q´ estará aplicado un momento del mismo
sentido.
Dado cualquier pórtico cargado (donde las barras que cortan al eje de simetría son
horizontales) que presente las condiciones de simetría mencionadas, tenemos que en los
puntos A, B etc. (de las barras) que pertenecen al eje de simetría se debe cumplir que:
vA = 0
vB = 0
NA = 0
NB = 0
MA =0
MB = 0
etc
Siendo v el desplazamiento vertical, N la directa y M el momento flector.
Demostración:
Tenemos una estructura cualquiera, que cumple las condiciones de ESCAS. La
llamaremos Estructura 1 en este análisis. Para visualizar mejor el razonamiento lo
veremos a través de una estructura particular como la de la siguiente figura. Sin
embargo el razonamiento empleado puede ser aplicado a cualquier otra estructura del
mismo tipo.
Estructura 1
A
B
Al sistema de cargas de la Estructura 1 le llamaremos P1. Asociado a P1 existe un vector
de desplazamientos ∆1 y existen solicitaciones S1 que expresan las reacciones y
solicitaciones que tiene la Estructura 1 en cada punto. Luego consideremos la
Estructura 2, que se obtiene de cargar la misma estructura, con una carga P2 = -P1.
Puede verse fácilmente que este es también un caso de ESCAS.
30
Estructura 2
A
B
De esta manera, como el análisis que estamos realizando es elástico y teniendo en
cuenta que la suma de los dos estados no significa ninguna carga para la estructura (se
anulan las fuerzas aplicadas) y en consecuencia no significa ninguna solicitación ni
tampoco significa desplazamiento alguno de la estructura, para todo punto se cumplirá
que:
∆ 2 = − ∆1 y S 2 = − S1
Esta propiedad es válida para todo punto de la estructura y naturalmente lo es para los
puntos que pertenecen al eje de simetría.
Pero ahora observemos que la Estructura 2 es como observar a la Estructura 1 desde el
lado de atrás, ver siguiente figura.
Estructura 1
D'
E
E'
G
Estructura 2
D'
A=A' D
F
G'
B=B'
E
D A=A'
F'
F'
F
E'
G'
G
B=B'
31
En consecuencia, los desplazamientos verticales de los puntos del eje de simetría
deberán ser iguales en ambas estructuras. Como además debe cumplirse que sean de
signo contrario (como habíamos visto) resulta que deberán ser nulos.
En cambio los desplazamientos horizontales serán observados de uno y otro lado como
de sentido opuesto (resultando la misma condición que ya habíamos obtenido) y en
consecuencia pueden ser distintos de cero.
Los giros en los puntos del eje serán vistos de sentido contrario y en consecuencia
pueden tener también cualquier valor.
Por lo tanto, los desplazamientos verticales de puntos de la estructura que pertenecen al
eje de simetría son nulos.
Vemos ahora las solicitaciones en los puntos del eje de simetría utilizando las dos
estructuras. Consideremos una barra que corte al eje de simetría en un punto, y
analicemos las solicitaciones en dicho punto.
Tomando la Estructura 1, sabemos que por equilibrio se cumple:
M
A
donde M sería M1(A)
Para la Estructura 2 con la carga contraria tendríamos que tener el momento contrario o
sea que nuestro esquema sería:
M
A
Pero observando la Estructura 1 del otro lado (tendríamos la situación de la estructura 2)
el observador vería los momentos del mismo signo que los observados en la Estructura
1. Luego podemos concluir que el momento flector en el eje necesariamente tiene que
ser nulo.
De manera análoga llegamos a que, en dichos puntos, la directa trasmitida es nula.
Queda para el lector la tarea de realizar un análisis análogo al anterior y observar que el
cortante trasmitido en los puntos de la estructura que pertenecen al eje no tiene por qué
ser nulo.
Luego resulta que la única solicitación que se trasmite en el eje de simetría es el
cortante.
Si al eje llegaran dos barras inclinadas razonando análogamente se tendría que la única
fuerza que se trasmite es una fuerza vertical.
32
A continuación vemos un primer caso de carácter general de problemas de este tipo.
Supongamos que tenemos una estructura ESCAS como la que se indica en la figura
siguiente.
A
B
Si resolvemos cortar la estructura por el eje de simetría y analizar la mitad de la
estructura tendremos que el esquema que resulta es el indicado en la figura siguiente:
X1
X2
Solo tendremos dos fuerzas incógnitas pues habíamos visto que la fuerza horizontal y el
momento flector eran nulos.
Pero además la condición que se debe cumplir es que los dos desplazamientos verticales
sean nulos o sea que la derivada de la energía de deformación en relación a X1 y en
relación a X2 deberá ser nula.
De esta manera se obtiene un sistema de dos ecuaciones con dos incógnitas. De haber
tomado la estructura original completa hubiéramos tenido un sistema de 6 ecuaciones
con 6 incógnitas.
33
Un segundo caso particular es cuando existe una carga aplicada en el eje de simetría. En
este caso si fuera una fuerza vertical por razones de antisimetría de las cargas tendría
que haber una fuerza igual y de sentido contrario aplicada en el mismo punto. Luego se
anularían y en consecuencia no puede haber ninguna fuerza vertical aplicada en el eje.
En cambio si se tratara de un momento la fuerza antisimétrica sería un momento del
mismo signo. En este caso no se anulan las fuerzas y en consecuencia es posible que
exista un momento flector aplicado en un punto del eje. Del mismo modo si existiera
una fuerza horizontal la fuerza antisimétrica será una fuerza horizontal del mismo
sentido. De manera que no se anulan y en consecuencia también podría haber una fuerza
horizontal aplicada.
Veremos los dos casos posibles con un ejemplo concreto planteado en la figura
siguiente.
M
F
Nuevamente se puede subdividir el momento y la fuerza horizontal en dos mitades
aplicadas muy próximas al eje y una de cada lado. Cuando sean muy próximas al eje el
efecto terminará siendo el mismo que el de una carga aplicada en el eje.
X1
M/2
F/2
X2
34
En la figura anterior se muestra el esquema de la estructura que deberá ser estudiada,
donde se mantiene las incógnitas hiperestáticas y se agregan la mitad de las fuerzas
aplicadas en el eje de simetría.
Un tercer caso es cuando se da la situación particular en que hay una barra que
pertenece al eje de simetría como el que se indica en la figura siguiente.
A
B
barra BC
Inercia: I
C
En este caso, dado que no hay desplazamientos verticales en el eje de simetría, tampoco
habrá directa en la barra BC. Sí puede haber desplazamientos horizontales y giros o sea
que podrá haber cortante y momento flector.
A estas solicitaciones contribuirá el lado izquierdo y el derecho con la misma magnitud
y sentido. En la medida que tomamos la mitad de la estructura, y en consecuencia
también la mitad de las cargas para mantener el efecto de la barra del medio, es
necesario tomarla con la mitad de la inercia. De esa manera se obtienen los mismos
resultados que con la estructura completa.
barra BC: tomo I'=I/2
C
NBC=0
35
Un cuarto caso es la situación particular cuando luego de realizar el corte de la
estructura se obtiene un mecanismo como se indica en la figura siguiente.
A
B
Teniendo en cuenta que no hay desplazamiento verticales de los puntos del eje, se puede
agregar en uno de ellos un apoyo deslizante para conformar una estructura isostática.
Solo quedará una sola fuerza incógnita como se indica en la figura siguiente.
X2
Condiciones de Simetría – Otros Casos
Si bien los casos más usuales de simetría son los anteriores existen otros casos donde la
simetría no está referida a un eje de simetría ubicado en el plano.
Por ejemplo, la simetría de la estructura y de sus cargas puede ser en relación a un punto
del plano como se indica en la figura siguiente. La idea será nuevamente ver cómo se
estudia la mitad de la estructura
36
La simetría en relación a un punto es equivalente a decir que cuando se toma la mitad de
la estructura y se gira 180 grados en el plano se obtiene la otra parte de la estructura y
de las cargas. En la figura siguiente se puede observar en forma gráfica la anterior
afirmación.
A
C
C
C
A
A
Nuevamente para las fuerzas utilizaremos las condiciones de simetría y las de equilibrio
y para los desplazamientos las de simetría y las de compatibilidad.
A
C
X3
X2
X1
En principio podría haber en el punto C una fuerza horizontal, una vertical y un
momento flector. El esquema será el de la figura anterior.
Si hubiera una fuerza vertical, su simétrica en relación al punto C será una fuerza
vertical de sentido contrario. Estas dos fuerzas están en equilibrio y por lo tanto es
posible su existencia.
37
Si hubiera una fuerza horizontal, el razonamiento sería totalmente análogo y en
consecuencia podría también existir.
En cambio si hubiera un momento flector su simétrico sería un momento flector del
mismo sentido. Luego resultaría que no estarían en equilibrio salvo que fuera nulo. En
consecuencia se concluye que el momento flector será cero en el punto C.
Un esquema de ambos análisis puede observarse en la figura siguiente.
A
X1
X3
X2
Simetría
X2
X3
C
B
X1
X3
Equilibrio
X2
X1
C
B
Veamos ahora la situación de los desplazamientos.
Si hubiera un desplazamiento horizontal, por razones de simetría debiera haber un
desplazamiento de igual magnitud y sentido contrario. Pero por condiciones de
compatibilidad el desplazamiento debe ser el mismo. Luego, los desplazamientos (tanto
en la dirección vertical como horizontal) serán necesariamente nulos.
Si hubiera un giro, por razones de simetría debiera haber un giro de la misma magnitud
y sentido. Esta condición es la misma que la que impone la compatibilidad de
desplazamientos y en consecuencia podrá haber giros.
Luego de realizado este análisis, concluimos que para resolver la estructura basta con
analizar el tramo AC, que es una estructura isostática, que presenta dos fuerzas incógnita
aplicadas en C. De esta manera, tenemos tres estados: el estado E0, el E1 y el E2.
Aplicando que la derivada de la energía de deformación respecto a X1 debe ser nula, y
que la derivada de la energía de deformación respecto a X2 también debe ser nula,
llegamos a un sistema de dos ecuaciones con dos incógnitas (X1 y X2), que podemos
resolver.
Un esquema de este análisis puede observarse en la figura siguiente.
38
Otros casos de simetría pueden presentarse y podrían ser resueltos de manera análoga.
16.
Comparación de energías
Es importante realizar una comparación de los diferentes tipos de energía de
deformación (según sea generada por flexión, directa, cortante o torsión) en condiciones
razonablemente similares a las que se producen normalmente. Para comparar las
energías utilizaremos fuerzas o momentos similares en las diferentes situaciones.
Flexión
Para calcular la energía de deformación producida por flexión tomaremos el caso
sencillo que se muestra en la figura. Esta misma situación será considerada para calcular
la energía de deformación producida por cortante.
El diagrama de momentos expresado analíticamente será:
M=
P
z
2
para
0≤ z≤
L
2
39
Luego podemos calcular la energía de deformación en la mitad de la barra, que será:
L/2
1 L/2 2
1 L/ 2 P2 2
P2 3
M
dz
=
z
dz
=
z
∫
∫
2 EI 0
2 EI 0 4
24EI 0
=
P 2 L3
24EI 8
Existiendo simetría, la energía de toda la viga será el doble, o sea:
1 P 2 L3 P 2 L3
=
UF =
24 EI 4 96 EI
Si aceptamos que la sección de la viga es rectangular con base b y altura h tendremos en
definitiva que:
P 2 L3
P 2 L3
UF =
=
96 EI 8Ebh3
Directa
La misma viga la someteremos a una directa de magnitud similar a la carga que
utilizamos en flexión:
En este caso como ya se ha observado se tendrá que:
P2 L P2 L
UD =
=
2 EA 2 Ebh
Comparación Flexión-Directa
Para comparar podemos realizar el cociente entre ambas energías:
P2L
U D 2 Ebh 4h 2
= 2 3 = 2
UF
P L
L
3
8Ebh
Si bien puede haber situaciones particulares diferentes, normalmente la luz de la viga es
bastante mayor que su altura. Aunque no hay una relación constante podemos suponer a
40
modo de ejemplo una relación razonable de 10 a 1. Luego tendremos que en estas
condiciones se tiene que:
U D 4h 2
L
= 2 < 0,04 si h <
UF
L
10
De lo anterior podemos concluir que para cargas equivalentes aplicadas sobre la viga en
flexión y directa y si la viga tiene dimensiones usuales entonces se tendrá que la energía
de deformación por directa puede ser prácticamente despreciada en relación a la
generada por flexión.
Cortante
Continuaremos analizando la misma viga y adoptaremos la misma carga supuesta para
el caso de la flexión. En este caso el cortante en toda la viga tiene el mismo valor
absoluto, o sea P/2.
Si consideramos la sección de la viga sometida a ese cortante y utilizamos la expresión
de Jouravsky, para una sección como la que se indica en la figura siguiente,
tendremos que la tensión rasante tiene la forma: τ =
Vµ
Ib
Donde
h/ 2
by 2
µ (ζ ) = ∫ y dA = b ∫ y dy =
2
ζ
Aζ
h/2
ζ

b  h2
=  − ζ 2 
2 4

Y, en consecuencia:

b  h2
V  − ζ 2 
2
2 4
 = 6V  h − ζ 2  = τ (ζ )
τ yz (ζ ) =

bh3
bh3  4

b
12
41
Teniendo en cuenta la ecuación constitutiva de un material elástico y lineal se verifica
que:
ε yz =
τ yz
2G
↔ T = λ [traza( D)]I + 2µD
donde µ = G
Al realizar el producto
ε yzτ yz =
τ yz
2
T : D aparece dos veces el producto:
2G
En función de ello la Energía de deformación tiene la forma:
h/2
1L
1 L
τ2
2
U = ∫ dz ∫ 2 dA =
∫ dz b ∫ τ dζ
2 0 A 2G
2G 0
−h / 2
Y sustituyendo la tensión rasante por la expresión que se obtuvo anteriormente se tiene
que:
2
1 L 2
36b h / 2  h 2
2
U=
∫ V ( z ) dz 2 6 ∫  − ζ  dζ
2G 0
b h −h / 2  4

Y observando que se cumple que:
h/2
2
 h2
h5
2


−
ζ
d
ζ
=
∫ 4

30

−h / 2 
que
P2
V ( z) =
4
2
y que
1 36b h5
3
=
2 6
2G b h 30 5Gbh
entonces
3 L 2
3P 2 L
3P 2 L
UC =
=
∫ V ( z ) dz =
5Gbh 0
5 * 4Gbh 20Gbh
Comparación Flexión-Cortante
El cociente entre las energías de deformación obtenidas es:
3P 2 L
U C 20Gbh 6 Eh 2
= 2 3 =
UF
P L
5GL2
8Ebh3
Teniendo en cuenta que, si ν es el modulo de Poisson, entonces:
G=
E
2(1 +ν )
42
Se tiene que:
U C 6 h2
=
2(1 + ν )
U F 5 L2
U C 12 h 2
(1 + ν )
=
UF
5 L2
Teniendo en cuenta que ν es menor que 0,5, se llega a una situación similar que en el
L
caso de la directa, donde si h = , entonces :
10
12
UC
=
(1,3) = 0,031
U F 500
Torsión
Para Sección Circular
En cursos anteriores se ha visto la torsión para secciones circulares. Repasaremos
algunos conceptos y veremos como pueden generalizarse a otras secciones.
En el caso de la sección circular sometida a un momento torsor puro sabemos que la
tensión rasante producida se ubica en el plano perpendicular al eje de la barra, es
perpendicular al radio y proporcional a la distancia al centro de la sección. O sea que se
cumple que:
τ = kr
Y en consecuencia el momento torsor será:
M t = ∫ τr dA = k ∫ r 2 dA
A
A
La integral de la expresión anterior no es otra cosa que la inercia torsional de la sección,
que se nota normalmente con la letra J. O sea que si R es el radio de la sección se
cumple que:
J = ∫ r 2 dA =
A
π
2
R4
Por otro lado se puede obtener que θ, que es el ángulo de barrenado (giro de una sección
en relación a otra que se encuentra a la unidad de distancia), se puede expresar en
función del momento torsor (Mt) la inercia torsional de la sección (J) y el módulo
elástico de corte del material (G) con la expresión:
θ=
Mt
GJ
Además, τ = Gθr , o sea que k = Gθ , donde la dimensión del barrenado es:
[θ ] = rad
m
43
El ángulo de giro ϕ de una sección en relación a otra que se encuentra a una distancia L
será proporcional a esa distancia y tendrá la forma:
ϕ = θL
La tensión rasante máxima se producirá en el perímetro de la sección. Si R es el radio de
la sección, tendremos que para r = R la tensión máxima será:
τ max = GθR =
donde Wt es el modulo resistente a torsión:
Wt =
Mt
Wt
J π 3
= R
R 2
Si sometemos una barra de longitud L a un momento torsor aplicado en sus extremos,
desde cero hasta un valor Mt, y trazamos el diagrama con el momento en el eje de las y
y el ángulo de giro en el eje de las x, tendremos que es lineal y que en consecuencia la
energía de deformación U tiene la forma:
1
U = M tϕ
2
Teniendo en cuenta que
ϕ = θL =
M t L , se obtiene que:
GJ
1 Mt 2L
U=
2 GJ
Para Sección Anular
Si la sección fuera anular (radio exterior Re y radio interior Ri) estaríamos en una
situación muy parecida.
Solamente tendríamos diferente que:
J = ∫ r 2 dA =
A
y que:
π
2
( Re 4 − Ri 4 )
J
Wt =
Re
El resto de las consideraciones y expresiones serían similares.
Para una Sección Cualquiera
En el caso de una sección cualquiera el problema es mas complejo y la distribución de
las tensiones rasantes también. No obstante ello los valores de J y Wt se pueden obtener
de tablas y se cumple también que:
M
θ= t
GJ
ϕ = θL
M
τ max = t
Wt
y
1 Mt 2L
U=
2 GJ
Las tensiones rasantes máximas están también en algún punto del perímetro.
44
Comparación Flexión-Torsión
Compararemos una viga sometida a un momento flector constante Mf y a un momento
torsor constante Mt. En este caso se tiene que:
2
2
1Mf L
UF =
2 EI
1 Mt L
UT =
2 GJ
Si para comparar hacemos los momentos torsor y flector iguales tendremos que:
U T EI
=
U F GJ
y colocando G en función de E se tiene que:
U T EI
I
=
2(1 + ν ) = 2(1 + ν )
U F EJ
J
Si observamos que I y J son del mismo orden tendremos que las dos energías de
deformación también lo son.
Conclusión
Podemos concluir que para vigas de dimensiones habituales (relación entre la longitud y
la altura del orden de 10 o mayor), sometidas a solicitaciones habituales, las energías de
deformación producidas por la flexión y la torsión son de orden equivalente. Ambas son
a su vez de un orden mayor que la producida por directa y cortante, que normalmente
pueden ser despreciadas.
17.
Emparrillados
Normalmente se denomina emparrillado a una estructura plana compuesta de vigas,
cargada con fuerzas perpendiculares al plano y/o momentos que representados
vectorialmente pertenecen al plano.
Debido a que las cargas no están en el plano el estudio de este tipo de estructuras es en
principio un problema espacial. Sin embargo puede ser simplificado como veremos a
continuación.
Consideraciones generales sobre los emparrillados
Para hacer este análisis partiremos del caso general, o sea, de una estructura plana
sometida a cualquier tipo de fuerza (cargas espaciales), y veremos qué simplificación
podemos hacer cuando solo actúan fuerzas como las que se indicaron anteriormente.
Cualquiera que puedan ser las fuerzas aplicadas las podemos separar en dos categorías.
Una primera categoría es la compuesta por las fuerzas que se encuentran en el plano y
los momentos normales al plano; a estas fuerzas las llamaremos fuerzas planas. Cuando
45
solo actúan fuerzas de estas características se trata de un problema plano con cargas
planas que ya ha sido estudiado.
La segunda categoría estará compuesta por las fuerzas perpendiculares al plano y los
momentos contenidos en el plano. A estas fuerzas les llamaremos fuerzas no planas.
Cuando solo actúan fuerzas de este tipo estamos en el caso que nos interesa estudiar,
que el caso de un emparrillado.
Es claro (en el caso general de cargas espaciales) que cualquier fuerza (o momento)
genérico que puede aplicarse sobre la estructura, puede ser descompuesta(o) en la suma
de una(o) de la primer categoría más una(o) de la segunda categoría.
De la misma forma cuando eliminamos apoyos o cortamos la estructura para generar las
incógnitas hiperestáticas éstas se pueden elegir separándolas en la parte plana y la parte
no plana.
Luego el vector de cargas aplicadas P puede ser descompuesto en dos partes. Un vector
de fuerzas planas que llamaremos PP y un vector de fuerzas no planas que llamaremos
PNP . De la misma forma las incógnitas hiperestáticas X pueden ser descompuestas en su
parte plana XP y en su parte no plana XNP.
Por otro lado los desplazamientos correspondientes a las fuerzas planas resultarán
desplazamientos planos y los nominaremos ∆P; a los correspondientes a las fuerzas no
planas (que serán no planos) les llamaremos ∆NP .
Del mismo modo a los desplazamientos correspondientes a las incógnitas hiperestáticas
los llamaremos ∆XP y ∆XNP. Estos dos, cuando se impongan las condiciones de
compatibilidad de los desplazamientos, deberán ser cero.
Luego podemos decir que el sistema de ecuaciones puede ser expresado subdividiendo
la matriz de flexibilidad de la estructura fundamental en 16 submatrices, quedando de la
forma:
 ∆ P   F11 , F12 , F13 , F14  PP 



 
 0   F21 , F22 , F23 , F24  X P 
 ∆  =  F , F , F , F  P 
 NP   31 32 33 34  NP 
 0   F41 , F42 , F43 , F44  X NP 
Ya era conocido que las fuerzas planas (cualquiera que sean) no producen
desplazamientos fuera del plano. Luego deberá cumplirse que:
F31 = 0, F32 = 0, F41 = 0, F42 = 0
Por otro lado habíamos visto que la matriz de flexibilidad es siempre simétrica. De
acuerdo a ello deberá cumplirse que:
F13 = 0, F23 = 0, F14 = 0, F24 = 0
46
En función de lo anterior el sistema de ecuaciones se desacopla en dos sistemas
independientes que son:
 ∆ P   F11 , F12  PP 


  = 
F
,
F
X
0
   21 22  P 
y
 ∆ NP   F33 , F34  PNP 



 = 
F
,
F
X
0

  43 44  NP 
El primero relaciona los desplazamientos planos con las fuerzas planas (aplicadas e
incógnitas hiperestáticas) mientras que el segundo relaciona los desplazamientos no
planos con las fuerzas no planas (aplicadas e incógnitas hiperestáticas).
Del primer sistema resulta que:
F21PP + F22 X P = 0
∆ P = (F11 − F22 −1F21 ) PP
X P = −F22 −1F21PP
y
Análogamente para el segundo sistema:
F43 PNP + F44 X NP = 0
X NP = −F44 −1F43 PNP
y
∆ NP = (F33 − F44 −1F43 ) PNP
En definitiva el problema se desacopla en dos sistemas de ecuaciones independientes.
Por un lado se puede resolver con el primer sistema el caso de cargas planas sabiendo
que no aparecen reacciones, solicitaciones y tampoco desplazamientos no planos.
Por el otro se puede resolver con el segundo sistema el caso de cargas no planas
sabiendo que no aparecen reacciones, solicitaciones y tampoco desplazamientos planos.
Este es el caso de un emparrillado que estábamos queriendo resolver. Consideraremos
entonces para resolver este caso solamente reacciones tales que la fuerza sea
perpendicular al plano de la estructura y momentos que pertenezcan al plano. Asimismo
solo se consideraran los desplazamientos normales al plano y los giros cuyo vector
pertenece al plano. Estos momentos significarán para las barras de la estructura
momentos flectores que deforman la estructura fuera del plano y momentos torsores.
47
Ejemplo particular
Consideremos un ejemplo sencillo de emparrillado. Se trata de un balcón, compuesto
de material y sección constante, donde actúan dos cargas de magnitud P perpendiculares
al plano. La estructura se indica en la figura.
En este caso se observa que el plano que pasa por el punto medio C perpendicular a la
barra BD se convierte en un plano de simetría de la estructura y de las cargas. Esto va a
permitir simplificar el problema.
Razonando análogamente a los casos planos ya vistos se puede analizar las
características de las solicitaciones y desplazamientos en el punto C.
En primer lugar por tratarse de un emparrillado en cualquier punto de la estructura solo
pueden existir solicitaciones no planas. De esa manera en el punto C podría haber un
cortante perpendicular al plano de la estructura, un momento torsor y un momento
flector que deforma la estructura fuera del plano. Los desplazamientos posibles son los
correspondientes a esa solicitaciones, o sea, un desplazamiento perpendicular al plano
de la estructura, un giro que torsiona la barra y un giro producido por la flexión fuera
del plano.
Si cortamos un pequeño tramo de la barra BD a un lado y otro del punto C tendremos
que las fuerzas de cortante a un lado y otro del punto C debieran ser ambas en el mismo
sentido por razones de simetría del problema. Pero por otro lado por razones de
equilibrio debieran tener sentido contrario. Luego resulta que el cortante en el punto C
deberá ser nulo.
El mismo razonamiento se puede aplicar para el momento torsor. Por simetría debe
tener el mismo sentido pero por equilibrio debe tener sentido contrario y en
consecuencia es nulo también. El momento flector por razones de simetría tendrá
sentido contrario y por razones de equilibrio también. Luego puede ser distinto de cero.
48
En relación a los desplazamientos perpendiculares al plano por razones de simetría
deben tener el mismo sentido y por razones de compatibilidad también. Luego pueden
ser distintos de cero. Los giros de torsión de la barra por simetría deben tener el mismo
sentido y por compatibilidad también. También pueden ser distintos de cero. Los giros
de flexión por simetría deben tener sentido contrario y por compatibilidad deben tener el
mismo. Luego deben ser nulos.
Resumiendo la anterior se puede decir que el momento torsor y el cortante en C son
nulos y la única solicitación que existe en C es el momento flector. Como contraparte de
ello el giro flector es nulo y el giro torsor y el movimiento perpendicular al plano
pueden ser distintos de cero.
Luego si tomamos la mitad de la estructura y tomamos como incógnita el momento
flector en C tendremos un problema con una sola incógnita. Si no hubiéramos realizado
consideraciones de simetría el problema hubiera tenido tres incógnitas.
A continuación podemos construir los diagramas de momento flector y momento torsor
producidos por las cargas aplicadas (Estado de Cargas 0 produce en la barra k Mf0k y
Mt0k) y los producidos por un momento flector en C unitario (produce en la barra k mfk
y mtk) .
Razonando en forma similar al problema plano se tiene que:
2
2 Lk  M f 0 k m fk 
2 Lk  m
2 Lk  m m 
2 Lk  m 2 
∂U
dz + X ∑ ∫  fk dz + ∑ ∫  t 0 k tk dz + X ∑ ∫  tk dz = 0
= ∑ ∫ 
∂X k =1 0  Ek I k 
k =1 0  Ek I k 
k =1 0  Gk J k 
k =1 0  Gk J k 


Y realizando los cálculos:
49
2 Pl 2
2l
∂U
Pl 2
3l
=−
+ 0 + X(
+ 0) + 0 −
+ X (0 +
)=0
∂X
2 EI
2 EI
GJ
GJ
Finalmente despejando X se obtiene que:
Pl 2 2 Pl 2
EI

+
1+ 4
GJ
X = 2 EI GJ = Pl 
3l
2l
 3 + 4 EI
+

2 EI GJ
GJ





Estos apuntes fueron elaborados por:
Dr. Ing. Atilio Morquio
Ing. Agustín Spalvier
Colaboraron en la corrección:
Ing. Maria Laura Reboredo
50