CAPITULO 5 BIS. TORSION
Anuncio
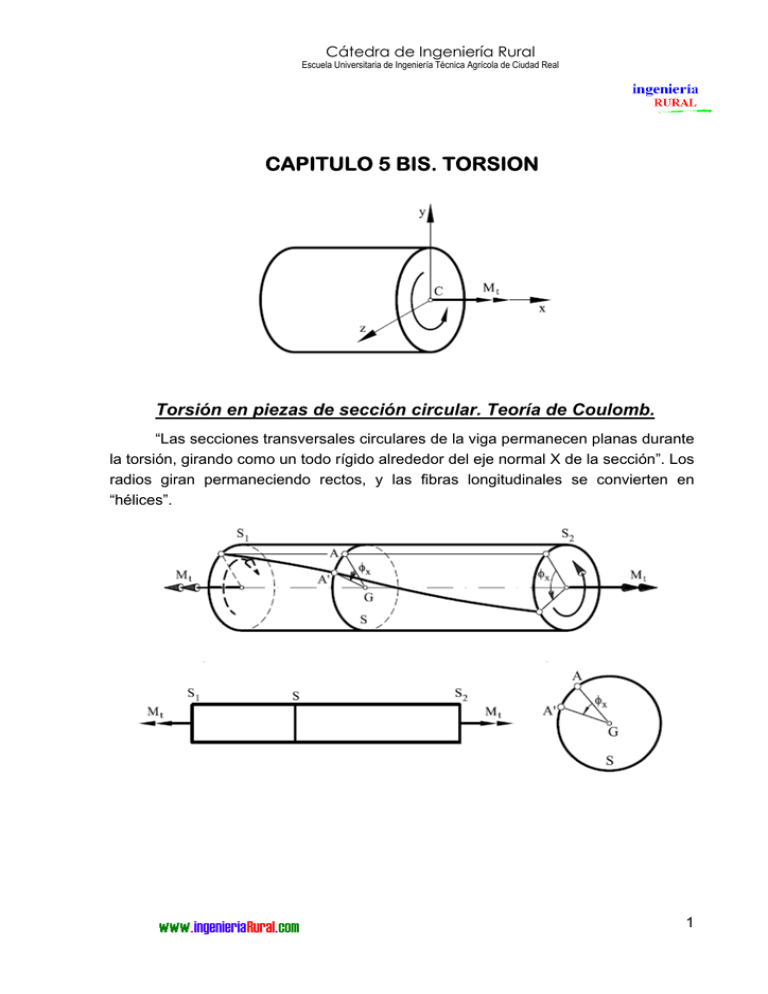
Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real CAPITULO 5 BIS. TORSION Torsión en piezas de sección circular. Teoría de Coulomb. “Las secciones transversales circulares de la viga permanecen planas durante la torsión, girando como un todo rígido alrededor del eje normal X de la sección”. Los radios giran permaneciendo rectos, y las fibras longitudinales se convierten en “hélices”. 1 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real γ = tan γ = CC ' ρ ⋅ dφ x = = ρ ⋅ θ , siendo: dx AC - φx el ángulo de torsión. - θ el ángulo de torsión por unidad de longitud, definido por θ = dφ . dx De acuerdo con Hook, τ = G ⋅ γ = G ⋅ ρ ⋅ θ , es decir, las tensiones tangenciales son proporcionales al radio. El momento resultante de las tensiones tangenciales debe ser igual al momento torsor actuante Mt. M t = ∫ ρ ⋅ τ ⋅ dS = ∫ G ⋅ θ ⋅ ρ 2 ⋅ dS = Gθ ∫ ρ 2 ⋅ dS =G ⋅ θ ⋅ I p , siendo Ip el momento polar de S S S inercia de la sección circular. El producto GIp es el módulo de rigidez torsional. θ= Mt M ρ τ ; pero ademas θ = , luego τ = t Gρ GI p Ip 2 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real El valor de tensión máximo se producirá en los puntos de ρ máximo. En una sección circular, estará en la circunferencia exterior, es decir, cuando ρ=r. El momento polar de un círculo es I p = π ⋅r4 2 2M t ⋅ r 2M t = . Por analogía a la flexión denominamos Módulo de torsión A⋅r π ⋅ r4 Ar Wt = , luego 2 τ max = τ max = Mt Wt En una sección circular hueca Ip = ∫ D/2 d/2 r 2 dA = ∫ Por tanto, Wp = D/2 d/2 r 2 2π ⋅ rdr = π ⋅ D3 ⎛ d4 ⎜⎜1 − 4 16 ⎝ D π ⋅ D4 ⎛ d4 ⎜⎜1 − 4 32 ⎝ D ⎞ ⎟⎟ ⎠ ⎞ 16M t ⎟⎟ , y τ max = d4 ⎠ 3⎛ π ⋅ D ⎜⎜1 − 4 ⎝ D ⎞ ⎟⎟ ⎠ Deformaciones en la torsión. θ= M Mt dφ , y además, θ = , por lo que dφ = t ds dx GI p GI p El giro total de la pieza entre dos secciones A y B será: φ=∫ B A Mt 1 dx = GI p GI p B ∫ M dx , A t donde la integral representa el área del diagrama de momentos torsores entre las secciones A y B. En el caso de momento torsor constante en toda la longitud de la pieza φ=∫ l 0 Mt M ⋅l dx = t GI p GI p 3 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real Torsión en piezas de sección prismática. Teoría de SaintVenant. Con la formulación estudiada hasta ahora, la distribución de tensiones en una sección prismática sería la de la figura de la izquierda. Esto supone que en puntos como C o P, existe una tensión rasante τn, lo cual no concuerda con la realidad. Puede comprobarse que en piezas prismáticas las secciones se alabean, con lo que no se cumplen los principios de Coulomb. Saint Venant dedujo que los mayores esfuerzos estaban en los puntos medios de los lados mayores, siendo su valor: Mt , siendo h y b los lados del prisma (h>b), y α un coeficiente que α ⋅ h ⋅ b2 depende de h/b. τ max = 4 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real El ángulo de torsión θ = Mt , siendo β un coeficiente que depende de h/b. β ⋅ G ⋅ h ⋅ b3 Torsión en piezas de paredes delgadas. Se demuestra, mediante la analogía de Prandl, que los esfuerzos cortantes apenas dependen de la curvatura de la sección transversal. Los esfuerzos y deformaciones en estas secciones son: τ max = θ= 3⋅ Mt , siendo s y t la longitud y el espesor de la sección. s ⋅ t2 3⋅ Mt . G ⋅ s ⋅t3 Torsión no uniforme. La teoría de Saint Venant supone que tanto el giro por unidad de longitud como el alabeo son uniformes en toda la longitud de la pieza. Pero esto en realidad no sucede en piezas que tengan alguna sección con alabeo impedido (p.e. empotramientos). 5 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real La distribución de tensiones en la sección libre, si la viga es suficientemente larga, es la indicada en la siguiente figura, que corresponde con las tensiones de Saint Venant. En la sección de empotramiento las tensiones de Saint Venant son nulas, puesto que el alabeo está impedido. Puede suponerse que las alas soportan un par de fuerzas F equivalentes al momento torsor, de valor F= Mt/h, que provocan una tensión cortante de valor τ max = 3⋅ Mt h⋅b⋅e Pero también soportan las tensiones normales producidas por el momento flector My = Fl, de valor σ max = F⋅l⋅b/ 2 6⋅ Mt ⋅l = e ⋅ b 3 / 12 hb 2 e Puede decirse que en piezas con secciones con alabeo impedido se desarrollan dos mecanismos resistentes totalmente diferentes para el momento torsor: - Uno debido a la torsión sin restricción de alabeo, denominado Momento de Saint Venant, Mv - Uno debido a la restricción de alabeo, al que llamamos Momento de Alabeo Impedido, Mw. De forma que Mt = Mv + Mw. Ambos mecanismos se distribuyen a lo largo de la pieza en función de las características de la sección y de la longitud de la pieza. 6











