Atomo y Tabla periódica

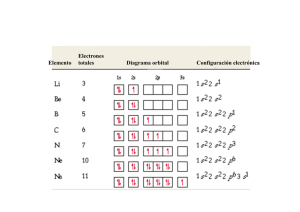
TEMA 2
ESTRUCTURA ATÓMICA Y CLASIFICACIÓN DE LOS ELEMENTOS
Modelos atómicos
El electrón. Modelo atómico de Thomson
Modelo atómico de Rutherford
Partículas fundamentales. Conceptos previos
Número atómico (Z)
Número másico (A)
Isótopos
Masa atómica
Espectros discontinuos. niveles de energía en los átomos
Espectros de emisión
Espectros de absorción.
Hipótesis de Planck
Modelo atómico de Bohr
Modelo atómico de Sommerfeld. numero cuántico secundario
Hipótesis de De Broglie
Principio de incertidumbre de Heisenberg
Determinismo y probabilidad
Números cuánticos
Orbitales atómicos
Distribución de electrones. Configuración electrónica
Principio de excusión de Pauli
Principio de máxima multiplicidad de Hund
Configuración electrónica
LA TABLA PERIÓDICA
Propiedades periódicas
1. Radio atómico y volumen atómico
2. Radio iónico
3. Energía de Ionización
4. Afinidad Electrónica
5. Electronegatividad.
6. Valencia.
MODELOS ATÓMICOS
Hasta finales del siglo XIX, con la teoría atómica de Dalton y la hipótesis de Avogadro
podía explicarse el átomo y su comportamiento en las reacciones químicas, pero diversos
experimentos han ido mostrando como los átomos están formados por diversas partículas
y que por lo tanto no son indivisibles como decía Dalton.
EL ELECTRÓN. MODELO ATÓMICO DE THOMSON
A finales del sigo XIX Geissler y Crooker realizaron varios experimentos en tubos llenos
con diversos gases a muy baja presión (muy similares a los fluorescentes actuales),
observando que conducían la corriente cuando se sometían a voltajes elevados.
Inicialmente se les llamó rayos catódicos porque parecían salir del cátodo (polo negativo)
y posteriormente Stoney los bautizó con el nombre de electrones. Tenían las siguiente
propiedades:
•
•
•
•
•
Salen perpendicularmente del cátodo y se mueven en línea recta en ausencia de
campos eléctricos y magnéticos
Los campos eléctricos y magnéticos los desvían, probando que tienen carga
eléctrica negativa.
Son capaces de mover las aspas de un molinete de mica si se ponen en su camino,
lo que prueba que son corpúsculos con masa
Cuando chocan con algunas sustancias provocan su luminiscencia y producen
calor, porque su energía cinética se transforma en energía térmica.
Impresionan las películas fotográficas
Thomson estudió los electrones en un tubo de vacío, precursor del tubo de televisión, que
estaba formado por un filamento que, al calentarse con un circuito auxiliar, emite
electrones por efecto termoiónico. Los electrones emitidos se aceleran hacia un ánodo
perforado mediante una gran ddp y se hacen chocar sobre una pantalla de sulfuro de cinc o
cualquier otra sustancia fluorescente.
Thomson, haciendo que no se desviaran al atravesar un campo eléctrico y otro magnético
perpendicular, consiguió medir la relación entre la carga y la masa del electrón, por lo que
recibió el premio Nóbel de física. Posteriormente Millikan (también Nóbel de física), en su
famoso experimento de la gota de aceite (consiste en suspender en un campo eléctrico una
gota de aceite previamente cargada) consiguió medir la carga del electrón y con ello calcular
su masa. Así resulta que e = 1,6 ⋅ 10 −19 C y me = 9,1 ⋅ 10 −31 Kg
Modelo atómico de Thomson: Este supuso que, puesto que en el tubo se había practicado el
vacío, los electrones debían provenir de los átomos del cátodo. En consecuencia los átomos
no son indivisibles como decía Dalton ya que, al menos están formados por electrones y algo
más bastante más pesado, puesto que la masa de los electrones es muy pequeña.
Puesto que los átomos son neutros, ese “algo más” debe tener carga positiva para
compensar a la negativa de los electrones. Thomson, en una carta a un amigo suyo, hacía
este mismo razonamiento y le decía que “los átomos deberían ser una esfera de materia
cargada positivamente, en cuyo interior estaban incrustados los electrones, de la misma
forma que las pasas en un bizcocho”. Por ese motivo a este modelo se conoce también
como el pastel de pasas.
MODELO DE RUTHERFORD
Becquerel había descubierto a final del XIX que ciertos elementos inestables, a los que se
les llamó radiactivos, trataban de estabilizarse emitiendo partículas α. β y radiación γ.
Rutherford y su ayudante Geiger estudiaban la naturaleza de las partículas α haciéndolas
incidir sobre una lámina muy delgada de oro y recogiéndolas sobre una pantalla
fluorescente de sulfuro de cinc.
Lo que observaron es que:
•
•
•
Casi todas las partículas atraviesan la lámina de oro sin desviarse
Algunas pocas de desvían
Algunas, muy pocas, rebotan que es lo más sorprendente.
Lo primero que se deduce es que el átomo está prácticamente hueco y por eso la mayoría
de las partículas α lo atraviesan sin desviarse. Debe tener una zona maciza muy pequeña
cargada positivamente que es la que desvía a las partículas α (que también son positivas) y
debe ser muy pequeña porque solamente unas pocas son las chocan con ella y rebotan.
Rutherford elaboró un nuevo modelo para el átomo para explicar los resultados de su
experimento, diciendo:
•
•
•
•
El átomo está formado por dos partes: núcleo y corteza.
El núcleo es la parte central, de tamaño muy pequeño, donde se encuentra toda la
carga positiva y, prácticamente, toda la masa del átomo, es decir los protones y
neutrones
Girando, a gran distancia, se encuentran los electrones, que deben girar para que la
fuerza centrífuga compense a la atracción eléctrica, de forma parecida al
movimiento de los planetas, donde la fuerza centrífuga compensa al peso. (Como
del núcleo a la corteza hay un espacio vacío muy grande, eso explicaría que la
mayor parte de las partículas alfa atraviesan la lámina de oro sin desviarse.)
En un átomo en estado normal, al ser neutro, tiene el mismo numero de protones
(+) en el núcleo que de electrones (−) en la corteza.
Rutherford descubrió los protones bombardeando nitrógeno con partículas α y puesto que
los protones tienen carga positiva, y en consecuencia deberían repelerse, Rutherford
postuló la existencia de otra partícula de masa similar que sería la responsable de darle
estabilidad. Años después Chadwick descubrió el neutrón y muchos años después Yukawa
dio la primera explicación de la estabilidad de los núcleos.
De acuerdo con la idea de Rutherford, el átomo de hidrógeno está formado por un protón
en el núcleo y un electrón girando a su alrededor a una distancia r, de tal manera que la
fuerza de atracción eléctrica se compense con la fuerza centrífuga (SR Inercial)
Felectr = Fcentrif
⇒
K
e2
v2
m
=
r
r2
de donde se puede despejar el radio de la órbita o bien la velocidad con la que debe girar
para mantenerse:
v=
Ke 2
mr
r=
Ke 2
mv 2
Como vemos, en el modelo de Rutherford cualquier radio es aceptable con tal que de gire
con la velocidad adecuada, con lo que los espectros atómicos deberían ser continuos.
La energía del electrón en la órbita, que será la suma de la cinética más la potencial (la Ep
es negativa porque las cargas del electrón y del protón tienen distinto signo: q=e y q´=−e)
1
e2
E = Ec + Ep = mv 2 − K
2
r
sustituyendo v
2
1  Ke 2 
e 2 1 Ke 2 Ke 2
1 Ke 2
E = m
−K
=
−
=−
2  mr 
r
2 r
r
2 r
La energía del electrón es función del radio de la órbita y aumenta con la distancia hasta
hacerse cero en el infinito (ten en cuenta que es negativa, lo que indica que una carga
negativa está ligada a una positiva. Lo mismo que ocurre entre las masas).
Al modelo de Rutherford pronto se le encontraron dos fallos importantes:
•
•
Si el electrón que es una carga gira debería radiar energía en forma de ondas
electromagnéticas y por tanto iría perdiendo energía hasta caer en el núcleo.
Puesto que todos los radios son posibles no explica que los electrones salten de
unos niveles a otros y en consecuencia no puede explicar las rayas espectrales.
PARTÍCULAS FUNDAMENTALES. CONCEPTOS PREVIOS
De acuerdo con lo anterior, en un átomo hay tres partículas fundamentales: protones y
neutrones, (a los que se llama indistintamente con el nombre de nucleones porque están en
el núcleo), y electrones en la corteza. Tienen las siguientes características:
protón
neutrón
electrón
Masa (uma)
Masa (Kg)
1,007597
1,008982
0,000549
1,67.10−27
1,67.10−27
9,1.10−31
Masa referida
al eletrón
1836
1838
1
Carga (C)
+1,6.10−19
0
−1,6.10−19
Carga referida
al electrón
+1
0
−1
Hoy día sabemos que de las tres partículas elementales que inicialmente se pensaba que
formaban los átomos, solamente lo es el electrón. Los protones y neutrones a su vez están
formados de otras partículas elementales llamadas quarks.
Número atómico (Z): Es el número de protones de un núcleo y es el que nos define al
elemento químico. (Un átomo en estado normal tiene igual número de protones y
electrones. Si pierde o gana electrones se convierte en un ión positivo o negativo del
mismo elemento, pero si perdiera o ganada un protón se transformaría en otro elemento
distinto, el anterior o posterior en la tabla periódica.)
Número másico (A): Es el número de protones y neutrones, es decir el número de
nucleones.
De acuerdo con esto, es evidente que el número de neutrones de un núcleo será:
N = Z−A
Lo núcleos se representan con el símbolo del elemento y un número en la parte inferior
que indica el número atómico (que es informativo, porque realmente es redundante) y otro
número en la parte superior que indica su masa:
A
Z
X
Z
XA
X AZ
Isótopos: Son aquellos núcleos que tienen el mismo número de protones, y por tanto
definen al mismo elemento, pero difieren en el número de neutrones y por tanto tienen
distinta masa. Tienen igual Z y distinto A. El hidrógeno tiene tres isótopos:
Es importante recordar que las propiedades químicas de los elementos vienen
determinadas por la disposición de los electrones de la última capa, así pues todos los
isótopos de un elemento se comportan químicamente igual y en este aspecto son
indistinguibles. Sin embargo tienen distintas propiedades físicas, empezando porque tienen
distinta masa y porque no todos tienen la misma estabilidad.
Ejemplo 1:
Un isótopo del oxígeno tiene número de masa igual a 18. ¿Cuántos protones, neutrones y
electrones tiene? ¿Y el ion O−2 de ese isótopo?
Al tratarse de oxígeno su número atómico no puede ser otro que Z=8 ya que, como hemos
dicho, el número atómico es el número de protones y define al elemento y viceversa.
Como A=18 y corresponde a la suma de protones y neutrones:
Protones
Neutrones
Electrones
=Z=8
= A – Z = 18 – 8 = 10
= nº Protones si es neutro = 8
El ion del oxígeno tiene su núcleo exactamente igual, es decir 8 protones y 10 neutrones,
pero su carga eléctrica no es nula, sino que tiene dos cargas negativas, es decir que tienen
2 electrones de más, y por tanto 8 + 2 =10 e−.
Masa atómica: Ya hemos visto que la mayoría de los elementos tienen varios isótopos en
proporción prácticamente estable, por eso la masa atómica que se tabula se calcula
haciendo la media ponderada de las masas de los isótopos según su abundancia relativa.
Ejemplo: 2
Se tienen los elementos
a) Isótopos
b) Isoeléctrónicos
228
90
X,
234
90
Y,
234
91
Z,
234
92
Q,
234
94
R +3 , razona cuales de ellos son:
a) Isótopos son aquellos núcleos que tienen el mismo número de protones, y por tanto
definen al mismo elemento, pero difieren en el número de neutrones y por tanto tienen
distinta masa, y de acuerdo en ello X e Y son isótopos al tener 90 protones y diferente
número de nucleones.
b) Isoeléctrónicos son aquellos átomos que tienen el mismo número de electrones, por
tanto átomos en estado fundamental de distintos elementos nunca serán isoelectrónicos,
pero sí pueden serlo sus iones. X e Y son isoelectrónicos porque son neutros y
corresponden al mismo elemento. Por otro lado, el átomo R al perder 3 electrones para
convertirse en su ión 3+ se queda solo con 91 electrones y en consecuencia es
isoelectrónico con Z.
Ejemplo 3:
La plata natural está formada por dos isótopos de masas 107 y 109 que se encuentran en
las proporciones de 56% y 44% respectivamente. Calcular al peso atómico de la plata.
Pat Ag =
107 ⋅ 56 109 ⋅ 44
+
= 107,88
100
100
las unidades, son uma/átomo o bien gr/mol
ESPECTROS DISCONTINUOS. NIVELES DE ENERGÍA EN LOS ÁTOMOS
Ya sabemos que cuando la luz blanca se hace pasar a través de un prisma se descompone
dando lugar a un espectro que contiene la totalidad de los colores desde el rojo al violeta,
por lo que se llama espectro continuo, mientras que si solo hay unos pocos se llama
espectro discontinuo.
Ese fenómeno, llamado dispersión de la luz, se debe a que las distintas radiaciones que
componen la luz, aunque todas tienen la misma velocidad en el vacío, tienen distinta
velocidad cuando viajan a través de otro medio, por ejemplo del vidrio, de manera que las
radiaciones de menor longitud de onda se desvían más y por eso se separan.
Las ondas electromagnéticas (OEM) son ondas transversales que no necesitan un medio
material para propagarse. Se dividen en varios grupos según su frecuencia (o según su
λ
longitud de onda, ya que ambas están relacionadas por la velocidad de la luz c = )
ν
Como puedes ver, las OEM de menor frecuencia, es decir de menor energía son las ondas
de radio y las de mayor los rayos gamma. También puedes observar como hay una
pequeña parte del espectro electromagnético que podemos detectar mediante el ojo. A esa
zona se le llama visible y según la frecuencia de la OEM la vemos de un color u otro, de
manera que realmente la diferencia entre una onda de radio, el color verde y un rayo X es
simplemente su frecuencia.
Un espectro de emisión es el espectro de la luz que emite un cuerpo, mientras que si
hacemos pasar la luz blanca a través del cuerpo y analizamos la luz que deja pasar, el
espectro se llama de absorción. Ambos son complementarios, quiere decir que los colores
que le faltan a uno son justamente los que tiene el otro.
En un espectro atómico:
•
•
•
El conjunto de líneas espectrales que se obtiene para un elemento concreto es
siempre el mismo, incluso si el elemento forma parte de un compuesto complejo,
es decir que cada elemento produce su propio espectro diferente al de cualquier
otro elemento, y por lo tanto el espectro de un elemento es como si fuera su huella
digital, por eso inicialmente los químicos alemanes Kirchoff y Bunsen comenzaron
a emplearlos como medio de análisis.
Los espectros contienen rayas agrupadas en series espectrales que van desde el IR
hasta el UV
Cada serie está formada por infinitas rayas cada vez mas juntas hasta llegar al
límite de la serie.
Si se descompone al luz emitida por un tubo de descarga lleno de hidrógeno, se obtiene su
correspondiente espectro, en el que se pueden distinguir sus series espectrales. Una de ellas,
la serie Balmer, cae dentro del visible, otra en el UV y el resto están en el IR.
El sueco Rydberg encontró empíricamente la relación que existía entre la longitud de onda
de cada raya en cada una de las series:
 1
1
1 
= RH  2 − 2 
n

λ
 i nj 
•
•
•
•
RH es la constante de Rydberg = 1,09.107 m−1
n1 y n2 son números enteros.
n1 determina la serie. Haciendo n1=1 se obtiene la serie Lyman, haciendo n1=2 se
obtiene la serie Balmer, con n1=3 la serie Paschen, etc
Limitando el valor de n1 para una serie concreta, el conjunto de rayas espectrales se
obtiene dándole a n2 valores enteros consecutivos al valor de n1, es decir n2 =
n1+1, n1+2, n1+3, ....
Serie
Lyman
Balmer
Paschen
Bracket
Pfund
ni
1
2
3
4
5
nj
2, 3, 4, ...
3, 4, 5, ...
4, 5, 6, …
5, 6, 7, …
6, 7, 8, …
Región del esp.
UV
Visible
IR
IR
IR
El modelo atómico de Rutherford era incapaz de explicar los espectros discontinuos de los
átomos porque según éste el electrón puede girar en cualquier órbita (cualquier valor del
radio es bueno) y por tanto el espectro debería ser continuo, y además porque al tratarse de
una carga acelerada debería radiar OEM de la misma frecuencia que la frecuencia de
revolución con lo que terminaría cayendo sobre el núcleo.
HIPÓTESIS DE PLANCK
El físico alemán Max Planck en una conferencia el 14 de diciembre de 1900, que es una
fecha histórica para la física, dijo que para poder explicar la radiación del cuerpo negro
había que desechar la idea de que los cuerpos pueden absorber y emitir energía de forma
continua.
Hay que admitir que la energía se absorbe y emite en forma de pequeños paquetes de
energía, que llamó “cuantos” (posteriormente Einstein los llamó fotones) y su energía es
proporcional a su frecuencia:
E = hν
h = cte. de Planck = 6,62 ⋅ 10 −34 J ⋅ s
Según esto, un cuerpo puede absorber o emitir un fotón, o dos, o tres, es decir n ⋅ hν
donde n es un número entero, lo que quiere decir que “la energía está cuantizada”.
•
Planck supuso que la radiación electromagnética era emitida por pequeños osciladores
submicroscópicos que solo podían vibrar con múltiplos enteros de cierta frecuencia ν,
y no con cualquiera, así que radiaban energía en múltiplos de hν.
•
•
Como el número de osciladores es enorme y cada uno de ellos oscila con una
frecuencia distinta, el cuerpo puede emitir todas las frecuencias y el espectro es
continuo.
Planck partiendo de esta idea, absolutamente nueva, consiguió una fórmula
empírica que reproducía exactamente la curva experimental de la radiación el
cuerpo negro.
Planck puso los cimientos de la física moderna, pero no recibió el premio Nóbel por su
descubrimiento del cuanto hasta varios años después, cuando Einstein hizo uso de éste
concepto para explicar el efecto fotoeléctrico, quedando la revolucionaria idea fuera de
dudas.
MODELO ATÓMICO DE BOHR
La deducción teórica de la ecuación de Rydberg vino de mano de Bohr, que propuso un
modelo atómico idéntico al de Rutherford, pero en el que el electrón solo puede girar en
unas órbitas estacionarias, donde no emite energía, y que son aquellas en las que el
momento angular del electrón es un múltiplo entero de h/2π.
L = rmv = n
h
2π
donde n es un número entero que toma valores 1, 2, 3 ... e indica la órbita y se llama
número cuántico principal.
Las transiciones electrónicas se producen absorbiendo y luego emitiendo un fotón de
energía igual a la diferencia de energía entre los niveles y dan lugar a los espectros
discontinuos. Así por ejemplo en el átomo de hidrógeno, que tiene un protón en su núcleo
y un electrón, el electrón estará girando en el nivel n=1, que es el nivel de menor energía.
Sin embargo podemos comunicar una energía a ese electrón y excitarlo, por ejemplo
calentándolo, iluminándolo o estableciendo una ddp y en ese caso la energía que adquiere
el electrón le hará saltar hasta una órbita más externa.
En la figura se muestra como un fotón excita al electrón, que inicialmente se encuentra en
el nivel mas bajo de energía, y lo manda hasta el nivel 4. Posteriormente vuelve a su
estado fundamental emitiendo un fotón correspondiente a la serie Balmer y otro a la serie
Lyman.
La energía de los fotones es igual a la diferencia de energía entre los niveles entre los que
salta:
 1
c
1 
∆E = E j − E i = hν = h = hcR H  2 − 2 
n

λ
 i nj 
R´= h c R H = 2,16 ⋅ 10 −18 J
Por ejemplo, el salto que se muestra en la figura, correspondiente a la segunda raya de la
serie Balmer, corresponde a un fotón de:
1 
 1
∆E = E 4 − E 2 = 2,16 ⋅ 10 −18  2 − 2  = 4,06 ⋅ 10 −19 J = 2,54eV
4 
2
E 4,06 ⋅ 10 −19
E = hν
⇒
ν= =
= 6,13 ⋅ 1014 Hz (azul)
h 6,62 ⋅ 10 −34
Ejemplo 4:
a) Razona si la siguiente afirmación es o no correcta: El ojo humano puede ver de color
azul una onda electromagnética de frecuencia igual a 4,0 ⋅ 1014 Hz y de color rojo otra de
frecuencia 7,0 ⋅ 1014 Hz .
b) La primera raya de la serie Lyman corresponde a un salto electrónico entre el nivel 2 y
el nivel 1. Calcula la diferencia de energía entre esos niveles, sabiendo que la frecuencia
de la raya es de 2,45 ⋅ 1015 Hz
Dato: Constante de Plack = 6,62 ⋅ 10 −34 J ⋅ s
a) La región correspondiente al visible del espectro electromagnético va desde el rojo, que es la
radiación menos energética y por tanto de menor frecuencia, hasta el violeta, que es la radiación
más energética. En consecuencia los valores de las frecuencias deben haberse cambiado, siendo
la frecuencia menor 4,0 ⋅ 1014 Hz la del rojo y la mayor 7,0 ⋅ 1014 Hz la del azul.
b) De acuerdo con la expresión de Plack, la energía correspondiente al fotón de luz
emitida por el electrón al saltar de un nivel a otro de menor energía viene dada por E = hν
por tanto es proporcional a la frecuencia:
∆E = E 2 − E 1 = h.ν = 6,62 ⋅ 10 −34 ⋅ 2,45 ⋅ 1015 = 1,62 ⋅ 10 −18 J = 10,13eV
Ejemplo
Para dos elementos de números atómicos Z1 = 11 y Z2 = 16.
a) Escribe, razonadamente, la configuración electrónica.
b) En un momento determinado el último electrón de ambos elementos se encuentra en el
subnivel 4s. Al volver al estado fundamental, uno de los elementos emite una raya roja,
mientras que el otro la emite amarilla. Razona a cual de los elementos corresponde cada raya.
MODELO ATÓMICO DE SOMMERFELD. NUMERO CUÁNTICO SCUNDARIO
El modelo de Bohr explicaba el espectro del átomo de hidrógeno pero no el de los demás
átomos con más electrones, donde aparecían rayas desdobladas, indicando que los niveles
estaban desdoblados.
Sommerfeld resolvió el problema diciendo que las órbitas podían ser circulares y elípticas
y que los desdoblamientos de las rayas se debían a que los niveles estaban desdoblados en
subniveles con órbitas con distintas excentricidades, introduciendo así el número cuántico
secundario (l) para designar el subnivel y que toma valores desde 0 hasta n−1, así:
nº cuántico principal (n)
n=1
n=2
n=3
n=4
nº cuántico secundario (l)
l =0
l = 0, 1
l = 0, 1, 2
l = 0, 1, 2, 3
subniveles
S
s, p
s, p, d
s, p, d, f
De esta forma se explica el desdoblamiento de las rayas espectrales. Por ejemplo, cuando
el electrón se excite y salte hasta el nivel n=3 puede alojarse en cualquiera de los tres
subniveles (s, p y d) que tiene, así que cuando vuelva a su estado inicial podrá emitir tres
fotones de energía muy parecida, pero distinta y por eso en el espectro aparecen tres rayas
muy juntas:
HIPÓTESIS DE De BROGLIE
Durante el primer cuarto del siglo XX la física tenía un dilema sobre la naturaleza de la luz
entre ondulatoria y corpuscular. Por una lado la radiación del cuerpo negro, el efecto
fotoeléctrico, el efecto Compton y la interpretación de los espectros atómicos apuntaban
hacia la naturaleza “cuántica” de la luz, mientras que los fenómenos de interferencias,
difracción y polarización evidenciaban su naturaleza ondulatoria.
En 1924, Luis De Broglie en su tesis doctoral hizo el siguiente razonamiento:
•
Si la luz está formada por corpúsculos, éstos se podrán caracterizar por su
momento lineal como cualquier partícula: p=mc con lo que la ecuación de
Einstein se podrá escribir como:
E = mc 2 = p c
•
Si la luz es una onda se podrá caracterizar por su longitud de onda:
E = hν = h
•
c
λ
Igualando ambas expresiones se deduce la relación entre la longitud de onda y el
momento lineal de los fotones asociados a ella:
λ=
h
p
o bien que
λ=
h
mv
De Broglie hizo extensiva su hipótesis a todas las partículas en general, y en particular a
los electrones diciendo: “A todo corpúsculo en movimiento se le puede asociar una onda,
cuya longitud de onda es inversamente proporcional a su momento lineal”
La hipótesis de De Broglie no tenía ningún apoyo experimental y por tanto debía
confirmarse, es decir habría que conseguir fenómenos de difracción con electrones, lo que
probaría que las partículas llevan asociada una onda.
Davisson y Germer, y poco después Thomson (hijo), consiguieron realizar experimentos
de difracción con electrones haciendo incidir un haz de electrones sobre una superficie
muy fina de níquel, obteniendo una figura de difracción similar a la que se obtiene por
difracción de rayos X y a partir de la que podía calcularse la longitud de onda asociada a
los electrones y que coincidía con la prevista por De Broglie.
De Broglie, mediante su hipótesis pudo demostrar lo que hasta entonces nadie había
podido: El porqué las órbitas del modelo atómico de Bohr estaban cuantificadas, es decir
que solo eran posibles aquellas en las que el momento angular del electrón es un múltiplo
entero de h / 2π
h
L = rmv = n
n=1, 2, 3, ....
2π
De Broglie dijo que si el electrón lleva asociada una onda, solo podrá girar en aquellas
órbitas para las cuales la onda sea estacionaria, lo que solamente puede ocurrir cuando la
longitud de la circunferencia sea un múltiplo entero de λ, porque en caso contrario la onda
se autodestruiría por sucesivas interferencias:
2 π r = nλ
Sustituyendo λ por el valor de De Broglie
2π r = n
h
mv
rmv = n
h
2π
organizando:
Una aplicación práctica de la dualidad onda−corpúculo es el microscopio electrónico
ideado por Müller. La limitación de un microscopio está en que no pueden resolverse
imágenes mas pequeñas que la longitud de onda de la luz que emplea. Cuando empleamos
luz del visible puede resolver hasta los 300 o 350 nm, así que no es posible ver algo que
mida menos de eso.
Los rayos X en principio podrían ser una solución, porque tienen longitudes de onda entre
10 y 0,01nm, pero no valen porque son muy difíciles de enfocar y dan lugar a imágenes
muy borrosas.
Los electrones sin embargo cuando se aceleran mediante un campo eléctrico pueden llegar
a tener longitud de onda muy pequeñas, de hasta 0,001nm, (recuerda que de acuerdo con
la expresión de De Broglie la longitud de onda es inversamente proporcional a la
velocidad de los electrones λ = h / m v ) y los electrones son fáciles de enfocar utilizando
campos eléctricos y magnéticos, como se hace en los tubos de TV.
Ejemplo 5:
Razone si la longitud de onda de De Broglie de los protones es mayor o menor que la de
los electrones en los siguientes casos:
a) ambos tienen la misma velocidad.
b) ambos tienen el mismo momento lineal?
a) Como sabemos la masa del protón es mucho mayor que la masa del electrón (algo más
de 1800 veces mayor), por tanto si el protón y el electrón tienen la misma velocidad la
longitud de onda del protón será menor:
λp =
h
mp v
λp
λe
λe =
=
h / mp v
h / me v
⇒
λp = λe
me
mp
⇒
λp < λe
h
me v
b) Si el protón y el electrón tienen el mismo momento lineal, ambos tendrán también la
misma longitud de onda asociada, ya que λ = h / p . Evidentemente, como
p = m p v p = m e v e para que ambas partículas tengan el mismo momento lineal deben
tener distinta velocidad, porque tienen distinta masa.
PRINCIPIO DE INCERTIDUMBRE DE HEISENBERG
Como es de suponer, es imposible realizar una medida sin interaccionar de alguna manera
con el sistema a medir, por ejemplo si para medir la temperatura de un líquido introducimos
un termómetro en él, éste intercambiará calor con el líquido que manera que cuando alcance
el equilibrio no nos dará la temperatura a la que realmente estaba el líquido. Pero claro el
termómetro es muy pequeño y el error que introduce en la medida es insignificante.
En el mundo microscópico, sin embargo, los errores son más importantes. Supongamos
que existiera un supermicroscopio con el que fuera posible ver el átomo de hidrógeno.
Como el poder de resolución del microscopio depende de la longitud de onda empleada y
es mas o menos igual a ella, resulta que tendríamos que iluminar al átomo con una luz de
o
o
aproximadamente λ = 1 A = 10 −10 m . Pero claro, un fotón de 1 A tiene una energía:
E = hν = h
c
3 ⋅ 10 8
= 6,6 ⋅ 10 −34
= 1,98 ⋅ 10 −15 J = 12375 eV
−10
λ
10
Si tenemos en cuenta que el potencial de ionización (energía necesaria para arrancarle un
electrón a un átomo) del átomo de hidrógeno es solo de 13,6 eV comprenderemos que la
interacción con el átomo sería tan grande que de ninguna manera podríamos verlo como es
en estado normal.
El principio de incertidumbre formulado por Wrener Heisenberg dice que “es imposible
conocer con exactitud y a la vez la posición y el momento lineal de una partícula. Cuanto
mayor sea la sea la precisión con que conocemos su posición, mayor será el error con que
podemos conocer su momento lineal y viceversa, de forma que el producto de las
incertidumbres siempre será mayor o igual que h/2π.”
∆x ⋅ ∆p ≥
h
2π
Esta incertidumbre nada tiene que ver con los instrumentos de medida, sino que es
intrínseca del hecho de medir.
Einstein extendió el principio de incertidumbre de Heisenberg a todas las parejas de
magnitudes conjugadas, es decir que tuvieran las mismas dimensiones que la posición por
el momento, es decir: ML2T−1, como ocurre con la energía y el tiempo, así que también
puede escribirse como:
h
∆E ⋅ ∆t ≥
2π
Ejemplo 6:
a) Calcular la longitud de onda asociada a un electrón que se mueve con una velocidad de
6.106 m/s
b) Calcular la longitud de onda asociada a una pelota de tenis de 100 g que se mueve con
una velocidad de 100 m/s. Compara los resultados obtenidos.
c) Si la velocidad del electrón y de la pelota estuvieran medidas con un error del 1% ¿Cuál
es el error con que podría determinarse la posición del electrón y de la pelota?. Compara
los resultados.
a) La velocidad del electrón se calcula teniendo en cuenta que:
λ=
o
h
6,62 ⋅ 10 −34
=
= 1,22 ⋅ 10 −10 m = 1,22 A
− 31
6
mv 9,1 ⋅ 10 ⋅ 6 ⋅ 10
b) En el caso de la pelota, la longitud de onda asociada sería:
λ=
o
h
6,62 ⋅ 10 −34
=
= 6,62 ⋅ 10 −35 m = 6,62 ⋅ 10 −25 A
mv
0,1 ⋅ 100
Como puede verse, la longitud de onda del electrón es comparable a la de los rayos X y es
del orden de las distancias interatómicas de los átomos en un cristal y por tanto es
apropiada para producir fenómenos de difracción y poner de manifiesto las propiedades
ondulatorias de la onda asociada al electrón.
Sin embargo, la longitud de onda asociada a la pelota de tenis es tan extremadamente
pequeña que en la naturaleza no existe nada comparable y por tanto, en la práctica, resulta
imposible poner de manifiesto la onda asociada a la pelota.
c) Supongamos ahora que las velocidades anteriores se han obtenido con un error del 1%.
En el caso del electrón el error cometido habría sido de:
∆v = 6 ⋅ 10 6 ⋅ 0,01 = 6 ⋅ 10 4 m / s
Así que el error con que habríamos medido el momento lineal sería:
∆p = m∆v = 9,1 ⋅ 10 −31 ⋅ 6 ⋅ 10 4 = 5,46 ⋅ 10 −26 Kg ⋅ m / s
así que:
∆x ⋅ ∆p ≥
h
2π
⇒
∆x ≥
h
6,62 ⋅ 10 −34
=
= 1,9 ⋅ 10 −9 m
− 26
2π ⋅ ∆p 2π ⋅ 5,46 ⋅ 10
En el caso de la pelota:
∆v = 100 ⋅ 0,01 = 1m / s
∆p = m∆v = 0,1 ⋅ 1 = 0,1Kg ⋅ m / s
∆x ⋅ ∆p ≥
h
2π
⇒
∆x ≥
h
6,62 ⋅ 10 −34
=
= 10 −33 m
2π ⋅ ∆p
2π ⋅ 0,1
Como vemos, en el caso del electrón la incertidumbre es del orden de las distancias
interatómicas, y por lo tanto es importante, pero en el caso de la pelota es absolutamente
despreciable porque no es ni siquiera del tamaño de un núcleo, es decir que a efectos
prácticos podríamos decir que sí podríamos determinar con precisión la posición de la
pelota.
En otras palabras, podemos decir que dada la pequeñez de la constante de Planck, la
incertidumbre en nuestro mundo macroscópico es despreciable, pero no ocurre así en el
mundo microscópico.
DETERMINISMO Y PROBABILIDAD
Como consecuencia del principio de incertidumbre de Heisenberg no podemos situar al
electrón en órbitas sencillas y bien definidas y además conocer su velocidad como puede
hacerse en el modelo de Bohr, que nos permite calcular el radio (posición) y la velocidad
(momento).
Schrodinger elaboró su mecánica cuántica ondulatoria partiendo de las ideas de De
Broglie y suponiendo que los estados estacionarios de los átomos corresponden a ondas de
materia estacionarias, a las que llamó función de onda ψ, que es una función de la posición
y del tiempo.
El significado de la función de onda ψ es probabilístico y nos da la probabilidad de
encontrar al electrón en un elemento de volumen dV:
P = ∫ Ψ 2 dV
V
Los valores de probabilidad oscilan entre 0 y 1. Es importante recalcar que ψ2 nos da una
medida de la probabilidad de encontrar al electrón en un volumen dado, es decir, no donde
está, sino donde es probable que esté, y por tanto no contradice el principio de
incertidumbre.
Supongamos el caso sencillo de una cuerda que está vibrando entre dos puntos. Como es
natural, esos dos puntos entre los que vibra serán nodos y además solo podrá vibrar con
unos determinados valores de λ, es decir que la longitud de onda está cuantizada ya que
solo puede tomar valores para los que la longitud de la cuerda sea siempre un múltiplo
entero de λ/2
λ
2
Por ejemplo dos modos posibles de vibración de la cuerda serían:
L=n
En el caso de una partícula encerrada entre esas paredes, la ecuación de esas ondas es la
que se representa por ψ, y la probabilidad de encontrar a la partícula entre esas paredes
viene dada por ψ2:
Como puedes ver, para n=1 es más probable que la partícula se encuentre en el centro, sin
embargo una interpretación clásica daría la misma probabilidad en cualquier lugar.
Aplicando estos mismo conceptos al átomo se obtienen unas regiones de máxima
probabilidad de encontrar al electrón que se llaman orbitales, por analogía con las
desechadas órbitas de Bohr.
Los orbitales son regiones del espacio, alrededor del núcleo, donde hay máxima
probabilidad de encontrar al electrón, por ejemplo en el desechado modelo de Bohr, el
electrón del hidrógeno está girando en una órbita perfectamente definida, mientras que
según el modelo de la mecánica cuántica no se puede saber exactamente donde está ni que
hace, sino que hay mucha probabilidad de encontrarlo dentro de una esfera, donde la
probabilidad es máxima para valores del radio predichos por Bohr:
NÚMEROS CUÁNTICOS
De la ecuación de Schrodinger se deducen tres números cuánticos que definen
inequívocamente cada uno de los orbitales atómicos, es decir cada orbital se define con
tres números cuánticos; n, l y m.
Los dos primeros ya fueron introducidos por Bohr y Sommerfeld. El número cuántico m,
llamado también número cuántico magnético, explica el efecto Zeeman que consiste en un
desdoblamiento de las rayas espectrales cuando espectro se obtiene en presencia de un
campo magnético. El número cuántico magnético toma valores desde –l ..0..+l
En cada orbital cabe un máximo de 2 electrones y estos de distinguen mediante el número
cuántico de spín, que toma valores de + 21 y − 12 e indica el sentido de giro del electrón
sobre sí mismo.
Así que resumiendo tenemos que un electrón se define con 4 números cuánticos:
•
Número cuántico principal (n) Indica el nivel y describe el tamaño del orbital, por
ejemplo: los orbitales para los cuales n=2 son más grandes que aquellos para los
cuales n=1. Puede tomar cualquier valor entero empezando desde 1: n=1, 2, 3, 4,
etc.
•
Número cuántico secundario del momento angular orbital (l) indica el subnivel.
Puede tomar valores naturales desde 0 hasta n−1 (siendo n el valor del número
cuántico principal). Por ejemplo si n=4, los valores de l pueden ser: l= 0, 1 ,2, 3.
Siguiendo la antigua terminología de los espectroscopistas, se designa a los
orbitales atómicos en función del valor del número cuántico secundario, l, como:
l=0
l=1
l=2
l=3
subnivel s
subnivel p
subnivel d
subnivel f
•
Número cuántico magnético (ml), determina la orientación espacial del orbital y es
el que determina de definir el orbital. Puede tomar valores enteros desde −l hasta
+l. Por ejemplo, si l=2, los valores posibles para m son: ml=−2,−1, 0, 1, 2
•
Número cuántico de espín (s), indica el sentido de giro del electrón y define a cada
uno de los dos electrones que caben en un orbital. Toma dos valores: +1/2 y −1/2.
•
Un orbital queda definido por los números cuánticos n, l y m. Mientras que un
electrón necesita para quedar definido los 4 números: n, l, m y s.
Como ejemplo vamos a escribir todos los posibles estados de un electrón que esté en el
nivel n=1 y en el n=2
n
l
m
s
orbital
1
0
0
1
0
0
−1, 0, +1
± 12
± 12
± 12 , ± 12 , ± 12
1s
2s
2px, 2py, 2pz
2
Nº
electrones
posibles
2
2
6
Ejemplo 7: E4B.S2009
Conteste a las siguientes cuestiones relativas a un átomo con Z=7 y A=14:
a) Indique el número de protones, neutrones y electrones
b) Escriba su configuración electrónica e indique el número de electrones desapareados en
su estado fundamental.
c) Cual es el número máximo de electrones para los que n=2, l=0 y m=0 ?
a) Teniendo en cuenta que el número atómico (Z), por definición, es el número de
protones y que en número de masa (A) es el número de protones+neutrones:
Protones
Neutrones
Electrones
=Z=7
= A – Z = 14 – 7 = 7
= nº Protones si es neutro = 7
b) Este apartado lo dejaremos para más adelante
c) Tres números cuánticos definen un orbital, y en cualquier orbital caben como máximo 2
electrones con spines +1/2 y –1/2. (por cierto que el orbital definido por los números
cuánticos n=2, l=0 y m=0 es el orbital 2s )
Ejemplo 8: E1A.S2006
Dados los conjuntos de números cuánticos: (2,1,2, ½); (3,1,−1, ½); (2,2,1,−½); (3,2,−2, ½)
a) Razone cuáles no son permitidos.
b) Indique en qué tipo de orbital se situaría cada uno de los electrones permitidos.
a) Como sabemos, los cuatro números cuánticos definen la posición de un electrón, pero
deben ser coherentes con los valores que pueden tomar, así que empezaremos desde el
número cántico principal viendo los posibles valores del resto:
(2,1,2, ½)
n = 2 → l = 0, 1
↓
m= −1, 0, 1
Imposible, el número cuántico l=1, no puede dar lugar a un número cuántico m=2, porque
m solo puede tomar valores desde –1 hasta +1.
(3,1,−1, ½)
(2,2,1,−½)
n = 3 → l = 0, 1, 2
↓
m = −1, 0, 1
↓
s = −1/2, +1/2
Correcto
n = 2 → l = 0, 1
Imposible, el número cuántico l toma valores desde 0 hasta n−1, y por tanto su valor
máximo sería 1, nunca 2.
(3,2,−2, ½)
n = 3 → l = 0, 1, 2
↓
m = −2, −1, 0, 1, 2
↓
s=−1/2, +1/2
Correcto
b) El electrón (3,1,−1, ½) está en el orbital definido por (3,1,−1) que corresponde a un
orbital 3p.
El electrón (3,2,−2, ½) está en el orbital (3,2,−2) que corresponde a un orbital 3d.
ORBITALES ATÓMICOS
Ya hemos dicho qué se entiende por orbital y qué los define:
•
•
•
Un orbital es una región del espacio, alrededor del núcleo, donde hay máxima
probabilidad de encontrar al electrón
Un orbital queda definido por los 3 números cuánticos n, l y m.
En cualquier orbital caben un máximo de 2 electrones con espines +1/2 y –1/2.
Ahora vamos a ver su forma, es la misma para todos los niveles, solo que cada vez son
mayores, así por ejemplo en subnivel s, que tiene simetría esférica, de los niveles n=1,
n=2 y n=3 sería:
m=0
s
un orbital simetría
l=0
esférica
p
l=1
d
l=2
f
l=3
m=−1, 0, 1
tres orbitarles de
dos lóbulos según
los ejes
m=−2, −1, 0, 1, 2
cinco orbitales
multilobulares
m=−3,−2,−1,0,1,2,3
siete orbitales
multilobulares
Por último nos queda ver como es la energía de los distintos orbitales:
•
•
•
La energía de los nivel aumenta con el nivel, como ya sabemos por el modelo de
Bohr, y por supuesto la energía de los subniveles asociados a cada nivel también va
aumentando.
Cuando un nivel se desdobla, parte de los subniveles que lo componen tienen
menos energía que él, mientras que otra parte de ellos son más energéticos.
Como los niveles cada vez están mas juntos, al desdoblarse a veces se solapan y
los subniveles superiores tienen menos energía que algunos inferiores:
Para recordar el orden energético de los subniveles ayúdate del siguiente esquema, en el
que cada fila representa un nivel y en él se han representado los distintos subniveles (solo
los necesarios) teniendo forma simétrica. Para averiguar la energía e cada subnivel no
tienes más que seguir el orden de las flechas:
Siguiendo las flechas obtendrás el orden siguiente: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s ...
DISTRIBUCIÓN DE ELECTRONES. CONFIGURACIÓN ELECTRÓNICA
El orden de llenado de los electrones en los átomos, llamado principio de construcción,
obedece a tres reglas básicas:
•
•
•
Los electrones tratan siempre de ocupar los niveles y subniveles de menor energía,
lo que supone una tendencia general de la naturaleza. Para recordar el orden
energético recordaremos la regla nemotécnica anterior.
Principio de excusión de Pauli: En cada orbital solo puede haber un máximo de dos
electrones con spines opuestos, lo que se suele enunciar también como que “en un
átomo no puede haber dos electrones con los cuatro números cuánticos iguales”.
Principio de máxima multiplicidad de Hund: Cuando varios electrones entran en un
mismo subnivel orientan sus espines de manera que haya el máximo de electrones
desapareados, es decir que sus orbitales se llenan primero con electrones del
mismo spín y cuando todos los orbitales están semillenos en la segunda vuelta
empiezan a aparearse con electrones de spín contrario.
Siguiendo estas tres sencillas reglas podemos construir una tabla de la siguiente forma:
•
•
•
•
Representamos mediante circulitos a los orbitales
Vamos dibujando hacia abajo los niveles y en ellos los subniveles que hay en cada
uno, así como el número de orbitales que hay en cada subnivel, recordando que
caben dos electrones: uno arriba con spín + 1 2 y otro abajo con spín − 1 2
Empezamos a numerar desde arriba siguiendo el orden de llenado (regla
nemotécnica) y teniendo en cuenta, que según la regla de Hund, cuando lleguemos
a un subnivel con varios orbitales, primero numeramos los de arriba y luego los de
abajo.
Hemos colocado sobre cada número el elemento del mismo Número Atómico
l=0
s
l=1
l=2
l=3
p
d
f
H
1
n=1
O
2
He
n=2
n=3
n=4
n=5
n=6
Li
3
B C N
5 6 7
O
OOO
4
Be
8 9 10
O F Ne
Na
11
Al Si P
13 14 15
Sc Ti V Cr Mn
21 22 23 24 25
O
OOO
OOOOO
12
Mg
16 17 18
S Cl Ar
26 27 28 29 30
Fe Co Ni Cu Zn
K
19
Ga Ge As
31 32 33
Y Zr Nb Mo Tc
39 40 41 42 43
O
OOO
OOOOO
OOOOOOO
20
Ca
34 35 36
Se Br Kr
44 45 46 47 48
Ru Rh Pd Ag Cd
64 65 66 67 68 69 70
Gd Tb Dy Ho Er Tm Yb
Rb
37
In Sn Sb
49 50 51
Lu Hf Ta W Re
71 72 73 74 75
Ac Th Pa U Np Pu Am
89 90 91 92 93 94 95
O
OOO
OOOOO
OOOOOOO
38
Sr
52 53 54
Te I Xe
76 77 78 79 80
Os Ir Pt Au Hg
96 97 98 99 100 101 102
Cm Bk Cf Es Fm Md No
Cs
55
Tl Pb Bi
81 82 83
Lr Rf
O
OOO
OOOOO
56
Ba
84 85 86
Po At Rn
Fr
87
n=7
O
88
Ra
n=8
O
OOO
103 104 105
La Ce Pr Nd Pm Sm Eu
57 58 59 60 61 62 63
Configuración electrónica: Es una especie de fórmula electrónica que indica los electrones
que tiene un elemento o ión, así como su disposición en los distintos niveles, subniveles y
orbitales. Para obtenerla no hay más que seguir las tres reglas básicas de llenado:
•
1 Que los electrones van entrando en los niveles y subniveles de menor a maor
energía, es decir en el orden 1s 2s 2p 3s 3p 4s 3d 4p 5s 4f … (para recordarlo
puedes utilizar el esquema energético)
2 Comienzas a colocar electrones, siguiendo el principio de exclusión de Pauli, y
se indican en forma de exponente del subnivel. La suma de los exponentes deberá
coincidir con el número de electrones a colocar que lógicamente será igual al
número atómico del átomo en estado fundamental.
3 Los electrones en cada subnivel entran siguiendo las reglas de máxima
multiplicidad de Hund, es decir, en primer lugar con los electrones del mismo spín.
•
•
Ejemplo 9:
Escribir la configuración electrónica de un elemento, sabiendo que Z=7 ¿Qué elemento es?
Para escribir la configuración electrónica de los estados fundamentales de cada átomo
debemos tener en cuenta (1º) que los electrones se van colocando en los subniveles de
menor a mayor energía (1s 2s 2p 3s 3p 4s 3d 4p 5s 4f …) y (2º) siguiendo el principio de
exclusión de Pauli y (3º) las reglas de máxima multiplicidad de Hund hasta completar el
número de electrones: 1s2 2s2 2p3 3s 3p 4s 3d 4p 5s 4f …
l=0
l=1
l=2
l=3
p
d
f
s
1
O
n=1
2
N
3
5
O
n=2
6 7
OOO
4
La configuración electrónica sería: 1s2 2s2 2p3 que obviamente corresponde a la posición
que debe ocupar el nitrógeno.
A veces se puede escribir de forma más detallada como 1s2 2s2 2px1py1pz1 (en este caso se
hace notar claramente las reglas de máxima multiplicidad de Hund)
Algunas veces se indica también escribiendo entre corchetes el gas noble previo y
completando únicamente los electrones que le faltan, es decir: [He] 2s2 2p3
Ejemplo 10: E1B.S2008
Para el ión Cl− (Z=17) del isótopo cuyo número másico es 36:
a) Indique el número de protones, electrones y neutrones.
b) Escriba su configuración electrónica.
c) Indique los valores de los números cuánticos de uno de los electrones externos.
a)
Protones
Neutrones
Electrones
= Z = 17
= A – Z = 36 – 17 = 19
= nº Protones + 1 = 17+1 = 18
b)
1
n=1
O
2
n=2
n=3
3
5
6 7
O
OOO
4
8
9 10
11
13 14 15
O
OOO
12
16 17 18
OOOOO
Cl Ar
La configuración electrónica (… siempre el mismo razonamiento) del cloro es Cl: 1s2
2s2p6 3s2p5
Y la configuración electrónica de su ión, que tienen un electrón más es:
Cl−: 1s2 2s2p6 3s2p6
Que coincide con la configuración electrónica del gas noble más próximo, que en este caso
es el Argón. Sin embargo, aunque el ión cloruro y el argón tengan el mismo número de
electrones y la misma configuración electrónica (se dice que son isoelectrónicos) no son
iguales, porque en sus núcleos siguen teniendo 17 protones el cloruro y 18 el argón, que
como dijimos es lo que realmente los identifica como tales elementos.
c) El electrón más externo, obviamente es el número 18, el que tienen de más, y sus
números cuánticos, como se deduce de la figura de la tabla, que como ves aquí también te
ayuda bastante, son:
l=0
m=0
n=1
l=1
l=2
O
(*)
m = −1 0 1
n=2
O
OOO
m =−2 –1 0 1 2
n=3
O
OOO
(*)
+ 12
OOOOO
− 12
n=3 (está en el nivel 3)
l=1
(está en el subnivel p)
m=1 (orbital px)
s=−1/2
Ejemplo 11: E3B.S2007
Dadas las configuraciones electrónicas:
A : 1s2 3s1 ; B : 1s2 2s3 ; C : 1s2 2s2 2p6 3s2 3p5; D : 1s2 2s2 2px2 2py0 2pz0
Indique razonadamente:
a) La que no cumple el principio de exclusión de Pauli.
b) La que no cumple el principio de máxima multiplicidad de Hund.
c) La que, siendo permitida, contiene electrones desapareados.
En primer lugar vamos a dibujar esas configuraciones electrónicas y después respondemos
a las preguntas:
a) El principio de exclusión de Pauli lo que dice es que no puede haber dos electrones con
los 4 números cuánticos iguales, dicho de una forma mas simple: que no puede haber dos
electrones ocupando el mismo sitio.
b) El principio de máxima multiplicidad de Hund dice que cuando varios electrones entran
en un mismo subnivel, sus orbitales se llenan primero con electrones del mismo spín, es
decir que primero llenaremos los de arriba y cuando haya entrado un electrón en cada
orbital empezaremos a aparearlos.
Configuración Disposición de
electrónica
electrones, según la c.e.
A : 1s2 3s1
2
B : 1s 2s
3
C : 1s2 2s2 2p6
3s2 3p5
D : 1s2 2s2 2px2
2py0 2pz0
Pauli
Nº electrones
desapareados
Hund
√
√
1
Litio
√
1
Cloro
No puede
haber 3
electrones en
un subnivel s
√
No se cumple
Se cumple,
porque el
porque no hay
último
2e con los 4 nº
electrón
cuánticos
debería tener
iguales
el mismo spín
que el anterior
LA TABLA PERIÓDICA
El primer intento de ordenar los elementos conocidos son las tríadas de Dobereiner, quien
en 1829 observó que había una serie de elementos que tenían propiedades muy parecidas y
que ordenándolos por su masa atómica, resultaba que la masa del elemento central era mas
o menos la media de la masa de los otros, así formó las siguientes tríadas:
Litio
Sodio
Potasio
Calcio
Estroncio
Bario
Azufre
Selenio
Telurio
En 1864, Newlands se dio cuenta de que si ordenada a los elementos por sus masas
atómicas, salvo con el hidrógeno, los elementos mostraban una cierta tendencia a repetir
sus propiedades cada cierto número.
Mendeleiev, en 1869, propuso un modelo agrupando a los elementos por sus masas
atómicas y ordenándolos en columnas según que tuvieran las mismas propiedades
químicas. Incluso no tuvo reparos para dejar huecos en su tabla prediciendo elementos que
aun no se conocían.
El modelo sistema periódico actual se debe a Henry Moseley, que demostró que muchas
de las imprecisiones de las ordenaciones anteriores podían subsanarse si los elementos se
ordenaban por su número atómico en lugar de por su masa.
Ordenándolos según su número atómico y plegándolos cada vez que se repiten sus propiedades
químicas el resultado fue elementos químicamente semejantes agrupados en familias o grupos y
en periodos.
A las columnas de la tabla periódica se les llama grupos y se numeran del 1 al 18. El
grupo es el que determina la configuración electrónica de la última capa.
A las filas de la tabla periódica se le llama periodos. El periodo coincide con el número
cuántico principal donde el átomo neutro tiene los electrones más externos.
Los elementos se clasifican en tres grandes grupos, sin contar el hidrógeno, según los
orbitales en los que están sus electrones de valencia, es decir los últimos:
•
Elementos representativos: s y p
s1
s2
s 2 p1
s 2 p2
s 2 p3
s 2 p4
s 2 p5
s 2 p6
•
•
Metales alcalinos, familia del Litio
Metales alcalino−térreos, familia del Berilio
Térreos o familia del Boro
Carbonoideos
Nitrogenoideos
Anfígenos, familia del Oxígeno
Halógenos, familia del Flúor
Gases nobles ( a excepción del Helio, que es 1s2)
Elementos de metales de transición: d
Elementos de metales de transición interna: f
grupo 1
grupo 2
grupo 13
grupo 14
grupo 15
grupo 16
grupo 17
grupo 18
grupos 3 a 12
Todos los elementos de un mismo grupo o familia tienen la misma configuración
electrónica en la última capa, es decir, tienen los últimos electrones dispuestos
exactamente de la misma forma, lo que nos lleva a decir que “las propiedades químicas de
un elemento residen en la disposición de sus últimos electrones, llamados también
electrones de valencia”. La diferencia de un elemento a otro de la familia está en el
periodo donde tiene los últimos electrones.
Las excepciones en la configuración electrónica del Como y del Cobre se deben a que:
1. Los orbitales s y los d del nivel anterior tienen energías muy parecidas
2. Las estructuras más estables son aquellas en las que los subniveles están llenos,
semillenos o vacíos. (Por ese motivo los gases nobles son muy estables, porque
tienen todos los subniveles llenos)
Cromo, debería ser 3d4 4s2 y es 3d5 4s1
Por ese motivo, al tener los electrones s y d energías muy parecidas, un electrón s salta al
subnivel d, y de esa forma ambos subniveles están semillenos, lo que es una estructura
estable. Eso mismo no ocurre, por ejemplo con el Carbono, porque en este caso los
subniveles s y p tienen energías más distintas.
Un paréntesis para repasar la Ley de Coulomb, que dice que, el módulo de la fuerza con que
se atraen o repelen dos cargas, según que tengan distinto signo o el mismo signo, es
directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado
de la distancia que las separa, siendo la dirección de la fuerza la recta que las une.
F=K
q ⋅ q´
r2
Puesto que el electrón tiene carga negativa y en el núcleo están los protones con carga positiva
se atraerán con una fuerza tanto mayor (1) cuanto mayor sea la carga nuclear o bien (2) cuanto
menor sea la distancia que los separa (radio del átomo).
PROPIEDADES PERIÓDICAS
De la disposición de los elementos en la tabla de Moseley, resulta que aparecen en
columnas formando familias todos los de la misma configuración y por eso no es de
extrañar que sus propiedades se repitan. Vamos a ver como varían algunas de ellas:
1. RADIO ATÓMICO y VOLUMEN ATÓMICO
No se puede calcular el tamaño exacto de los átomos debido, como hemos visto, a que la
mecánica cuántica considera al electrón dentro de una nube difusa (orbital) y no girando
con un radio definido como preveía Bohr. Sin embargo podemos definir el Radio atómico
de un elemento como la mitad de la distancia entre los centros de dos átomos vecinos.
El volumen atómico se define como el volumen que ocupa 1 mol de átomos del elemento
y por tanto se calcula como:
V=
masa 1 mol
Pm (gr )
=
densidad
ρ (gr / cm 3 )
Obviamente ambas magnitudes, el radio y el volumen atómico, varían correlativamente:
•
Dentro de una familia, aumenta hacia abajo, porque cada nuevo
elemento de la familia tiene los electrones dispuestos
exactamente igual, pero cada vez en una capa más externa y de
mayor energía. Además, porque los electrones de cada nuevo
elemento de la familia se encuentran con una capa llena más que
hace de pantalla.
•
A lo largo de un periodo, a primera vista, podríamos pensar que todos los átomos
son iguales porque todos los electrones entran en el mismo nivel, sin embargo a lo
largo del periodo el radio va disminuyendo, ya que aunque los nuevos electrones van
entrando en el mismo nivel del átomo (e incluso en un nivel inferior)
simultáneamente va aumentando la carga nuclear lo que hace que cada vez el núcleo
atraiga con más fuerza a sus electrones y por eso se contrae. No obstante, el gas
noble ya es mayor porque tiene demasiados electrones (la capa llena) y la repulsión
entre ellos pesa más que la atracción nuclear.
•
En el caso de los elementos de transición, como ocurre en general a lo largo de un
periodo, los volúmenes atómicos van disminuyendo hasta que llega un momento
en el que hay tantos electrones en la nueva capa que los apantallamientos mutuos y
las repulsiones se hacen importantes, hacen que aumenten de tamaño.
•
Si representamos el radio de los átomos en función del número atómico
obtendremos una gráfica similar a la siguiente
Ejemplo 1:
Ordena de mayor a menor tamaño a los átomos siguientes: Na, Be y Mg
Una vez situados estos elementos en el sistema periódico se ha de hacer uso de las
variaciones periódicas de esta propiedad ya comentadas.
Importante: En los comentarios a los contenidos de selectividad se indica que “no se
considera justificación las flechas que indican el orden de variación de las propiedades”,
es decir, no vale para nada decir simplemente que el tamaño en una familia aumenta hacia
abajo y en un periodo disminuye hacia la derecha, a menos que se acompañe de un
razonamiento en los términos anteriores.
•
•
Na (metal alcalino) y Mg (metal alcalino−térreo) ambos están en el mismo
periodo. En un periodo el tamaño disminuye hacia la derecha porque los electrones
entran en el mismo nivel a la vez que va aumentando la carga nuclear lo que hace
que cada vez el núcleo los atraiga con más fuerza y se contraiga. Es predecible que
rMg<rNa.
Be y Mg se encuentran en la misma columna (familia). En una familia el tamaño
aumenta hacia abajo porque tienen la misma distribución de sus electrones de
valencia, pero cada vez en una capa más externa. Es predecible que rBe<rMg.
Por tanto, el orden pedido sería: rBe<rMg<rNa.
Fíjate como hemos utilizado la situación en la tabla para razonar el tamaño, pero además
hemos añadido el porqué es así, y ese razonamiento es el que da validez a la respuesta
2. RADIO IÓNICO
El radio iónico es una magnitud muy importante para entender la estructura y estabilidad
de los cristales iónicos. Su tamaño varía lo mismo que el radio atómico, pero además
depende muchísimo de la carga del ión.
•
Los iones positivos son siempre más pequeños que los átomos de los que derivan
ya que al tener menos electrones y la misma la carga positiva en el núcleo éste se
contrae disminuyendo su tamaño
•
Los iones cargados negativamente son siempre mayores que los átomos de los que
derivan, ya que a la misma carga nuclear le cuesta más retener un mayor número
de electrones a lo que se suma el apantallamiento del resto de los electrones.
Ejemplo 2:
¿Cuál de los siguientes iones y átomos es el más grande: S2−, S, O2−?
•
Los aniones tienen mayor tamaño que los átomos de los neutros, porque teniendo
la misma carga positiva en el núcleo tienen electrones de más y por tanto les cuesta
más retenerlos. Es predecible que, rS2− > rS.
•
S y O son elementos que se encuentran dentro de la misma columna y por tanto,
tanto los átomos neutros como sus iones, tienen la misma distribución de sus
electrones de valencia, pero como el azufre está por debajo del oxígeno esos
electrones están en una capa más externa y por tanto su tamaño es mayor. Es
predecible que rS2− > rO2−.
•
Por tanto, el ion más grande es el ion S2−.
3. ENERGÍA DE IONIZACIÓN
Es la energía necesaria para arrancar un electrón a un átomo en estado gaseoso y
convertirlo en un ión positivo. Aunque la unidad internacional de energía es el julio, suele
expresarse en electrón−voltios/átomo (eV/átomo).
X ( g ) + E i → X (+g ) + e −
A la energía necesaria para arrancarle un segundo o tercer electrón se le llama segundo,
tercer potencial de ionización…
Como es natural, cuanto más fácil sea quitarle un electrón a un átomo, tanto menor será su
energía de ionización. Si tienes en mente la ley de Coulomb comprenderás que la fuerza
con que el núcleo atrae al electrón es mayor cuando mayor sea la carga nuclear y, cuanto
menor sea la distancia del electrón al núcleo, o sea su tamaño, así que:
•
Dentro de una familia disminuye hacia abajo debido a que el tamaño de los átomos
es cada vez mayor, con lo que los electrones de valencia están cada vez más lejos y
menos atraídos y por otro lado porque al tener más electrones aumenta el efecto
pantalla.
•
En un periodo tiende a aumentar al hacerlo el número atómico, ya que los átomos
son cada vez más pequeños y tienen mayor carga nuclear con lo que los electrones
están más retenidos. No obstante hay excepciones muy curiosas que ahora
veremos.
•
En cada periódico, los gases nobles tienen las energías de ionización más elevadas.
Estos gases son elementos muy estables y sólo los más pesados de ellos muestran
alguna tendencia a unirse con elementos para dar compuestos.
Las energías de ionización, en eV, de los elementos del segundo periodo son:
Li
5,4
Be
9,3
B
C
N
O
F Ne
8,3 11,3 14,5 13,6 17,4 21,5
Observaciones:
•
El Litio (y los de su misma familia) tiene el valor más pequeño porque al perder su
electrón pasaría a tener la configuración de un gas noble (en este caso del helio)
•
Por la misma razón, la segunda energía de ionización del Berilio, Magnesio, etc es
pequeña, porque estos elementos al perder dos electrones pasan a tener
configuración de gas noble. Sin embargo la segunda EI de Litio, Sodio, etc es muy
grande porque supone romper esa estructura de gas noble.
•
Como ya hemos razonado antes, a lo largo de un periodo la EI va aumentando
hacia la derecha pero, como vemos, esa tendencia se rompe con el Boro y con el
Oxígeno. La explicación es muy sencilla: Recuerda que la configuración del Boro
es 2s2p1 y que la del oxígeno es 2s2p4 y por tanto cuando pierdan un electrón sus
subniveles pasan a estar “llenos, semillenos o vacíos”, que como sabemos son las
estructuras más estables.
•
El flúor (y el resto de halógenos) tienen una EI muy elevada, además de porque
son mas pequeños y por tanto sus electrones están más retenidos, porque solo les
falta 1 electrón para tener la configuración de un gas noble, así que su tendencia no
es precisamente a perder uno, sino todo lo contrario.
La energía de ionización es una magnitud muy importante puesto que nos permite conocer
la tendencia de los átomos a formar iones positivos y a entender el comportamiento de los
enlaces iónicos.
Como cuanto menor sea la EI mayor será la tendencia a formar iones positivos
(electropositividad), podemos entender que los metales alcalinos y los alcalinotérreos
formen iones positivos (los que están a la izquierda de la tabla), pero que los halógenos no
los formen (los que están a la derecha).
Ejemplo 3: E3A.S2009
La siguiente tabla proporciona los valores de las energías de ionización (eV) de tres elementos
1ª
2ª
3ª
4ª
Li
5,4
75,6
122,5
−−−
Na
5,1
47,3
71,9
99,1
K
4,3
31,8
46,1
61,1
a) Por qué la primera energía de ionización disminuye del litio al potasio?
b) Por qué la segunda energía de ionización de cada elemento es mucho mayor que la
primera?
c) Por qué no se da el cuarto valor de la energía de ionización del litio
a) Dentro de una familia disminuye hacia abajo debido a que el tamaño de los átomos es
cada vez mayor, con lo que los electrones de valencia están cada vez más lejos y menos
atraídos y por otro lado porque al tener más electrones aumenta el efecto pantalla.
b) Teniendo en cuenta que la configuración electrónica en la última capa de los alcalinos
es ns1, se explica que la primera EI sea pequeña porque al perder el único electrón que
tienen en la capa más externa pasan a tener estructura del gas noble que le precede, pero
quitarle un segundo electrón supone precisamente romper esa estructura que es muy
estable.
c) El Litio tiene solamente 3 electrones (1s2 2s1) y por tanto es imposible quitarle un
cuarto que no existe
Ejemplo 4: E5B.S2009
Considerando las configuraciones electrónicas de los átomos: A (1s2 2s2 2p6 3s1) y
B (1s2 2s2 2p6 6p1). Razone si las siguientes afirmaciones son verdaderas o falsas:
a) A y B representan elementos distintos.
b) Se necesita energía para pasar e A a B.
c) Se requiere una menor energía para arrancar un electrón de B que de A.
a) El elemento A es un metal alcalino, concretamente el Sodio en su estado fundamental.
El elemento B también corresponde al sodio, pero su electrón de valencia se encuentra
excitado porque en lugar de estar en el subnivel 3s está en el 6p, que obviamente es de
mayor energía. Cuando ese electrón retorne al nivel vacío de menor energía (3s) emitirá un
fotón de energía E=hν, igual a la diferencia de energía entre ambos subniveles.
b) Evidentemente, puesto que el subnivel 6p es más energético que el 3s, el electrón no va
solo, hemos de aportarle la energía equivalente a la diferencia de energía entre ellos.
c) Claro, puesto que arrancar un electrón significa mandarlo al nivel infinito, será más
fácil mandarlo del 6º al infinito que desde el 3º. El ahorro energético que tendríamos es
igual a la diferencia de energía entre ambos subniveles.
Ejemplo: 5
Ordena de menor a mayor energía de ionización a los elementos siguientes: Ne, Na, P, Ar y K.
•
•
•
•
Na, P y Ar están en la misma fila de la tabla periódica, por lo que EINa<EIP<EIAr.
Ne y Ar son de la misma familia, gases nobles, y como el Ar tiene un volumen
mayor sus electrones de valencia estarán menos retenidos, así que su EI será menor
que la del Ne. Es esperable que EIAr<EINe.
De igual modo, el Na y el K que son también de la misma familia, metales
alcalinos: EIK<EINa.
A partir de estas observaciones concluimos que las energías de ionización siguen el
orden EIK<EINa<EIP<EIAr<EINe.
4. AFINIDAD ELECTRÓNICA
La Afinidad Electrónica, también llamada Electroafinidad, es la energía desprendida
cuando un átomo en estado gaseoso capta un electrón y se convierte en un ión negativo.
Suele expresarse en electrón−voltios/átomo (eV/átomo).
X ( g ) + e − → X (−g ) + E af
Todos los elementos tienen una energía de ionización, porque por muy sujetos que tengan sus
electrones siempre podremos suministrar la energía necesaria para arrancarlos.
Sin embargo, no todos los elementos tienen una energía de afinidad electrónica, porque
muchos de ellos no van a captar un electrón por más que queramos. Es el caso de los gases
nobles que ya tienen la estructura más estable posible, o los metales alcalinos o
alcalinotérreos cuya tendencia es la contraria como hemos visto antes.
La afinidad electrónica varía exactamente de la misma forma que la energía de ionización,
ya que por las mismas razones que un átomo se opone a perder un electrón, por las mismas
tiende a ganarlo, es decir, cuando sea pequeño y su carga nuclear grande
•
Dentro de una familia disminuye ligeramente hacia abajo debido a que el tamaño de los
átomos es cada vez mayor y el núcleo presenta menor atracción por el nuevo electrón.
•
En un periodo aumenta al hacerlo el número atómico, ya que los átomos son cada vez
más pequeños y el núcleo tiene mayor atracción sobre el nuevo electrón.
No obstante de lo anterior, los elementos muy pequeños tienen una afinidad electrónica
algo menor de lo esperado debido a que ese tamaño tan pequeño hace que el electrón que
entra se repela por los electrones que ya hay.
Las afinidades electrónicas en eV de algunos elementos son:
Fíjate que los metales alcalinotérreos tienen AE cero, lo mismo que los gases nobles,
porque tienen estructuras muy estables y por ese motivo no quieren un electrón más que
venga a desestabilizarlos. Los primeros son ns2 np0 así que tienen un subnivel lleno y otro
vacío, y los gases nobles ns2 np6 tienen la última capa llena.
Fíjate también que la familia del nitrógeno tiene valores anormalmente bajos,
precisamente porque todos ellos tienen configuración ns2 np3, es decir tienen un subnivel
lleno y otro semilleno, lo que es muy estable y por tanto no tienen ningún interés en
admitir otro electrón, especialmente el nitrógeno.
5. ELECTRONEGATIVIDAD.
La dificultad para medir la afinidad electrónica ha llevado a definir una nueva magnitud
llamada electronegatividad. La electronegatividad mide la tendencia que un átomo “que se
encuentra enlazado” tiene para atraer a la pareja de electrones del enlace.
Hay varias escalas para medir la electronegatividad:
•
•
La escala de Mulliken se hace tomando como valor la media aritmética de la
energía de ionización y de la afinidad electrónica.
La escala de Pauling, que es la más utilizada, toma valores entre 0,7 para el Cesio y
4 para el flúor. Se calcula a partir de las energías de enlace.
Puesto que la electronegatividad está íntimamente relacionada con le energía de ionización y
con la afinidad electrónica, varía como ellas, es decir que aumenta hacia la derecha de la tabla y
disminuye hacia abajo en una familia porque aumenta al disminuir el tamaño de los átomos.
La electronegatividad sirve para clasificar los elementos en metales o no metales, según
sean poco o muy electronegativos. Los no metales, por ejemplo son los que, como hemos
visto, tienen los mayores valores de energía de ionización, de afinidad electrónica y de
electronegatividad y por eso tienden a formar iones negativos captando electrones y son
oxidantes como veremos más adelante.
Además la electronegatividad es un concepto importantísimo para comprender el tipo de
enlace que tendrá lugar entre dos átomos:
•
•
•
El enlace entre átomos iguales o de muy parecida electronegatividad es apolar,
como ocurre por ejemplo en la molécula de oxígeno, O2.
El enlace entre átomos que tienen electronegatividades muy distintas es iónico,
como ocurre por ejemplo en el cloruro sódico, NaCl,
En los casos intermedios el enlace es covalente con un componente más o menos
polar, dependiendo de la diferencia de electronegatividades, como por ejemplo en
el cloruro de hidrógeno, HCl.
Ejemplo 6: E2A.S2008
El número de protones en los núcleos de cinco átomos es el siguiente:
A = 9; B = 16; C = 17; D = 19; E = 20
Razone:
a) ¿Cuál es el más electronegativo?
b) ¿Cuál posee menor energía de ionización?
c) ¿Cuál puede convertirse en anión divalente estable?
a) Lo primero que vamos a hacer es situarlos en la tabla periódica:
Puesto que la electronegatividad aumenta hacia la derecha de la tabla porque el volumen
de los átomos es menor y disminuye hacia abajo porque el volumen aumenta, podemos
decir que el elemento más electronegativo es el flúor, el de número atómico Z=9. Además
precisamente a éste elemento Pauling le asigno el máximo valor de 4,0
b) La energía de ionización varía igual que la electronegatividad, aunque son conceptos
distintos, pero lo motivos por los que un átomo atrae electrones son los mismos por los
que se resiste a que se los quitemos, por eso aumenta hacia la derecha porque los átomos
se contraen y disminuye en una familia porque cada vez tienen mayor tamaño. (Esto, claro
con las excepciones que hemos comentado, de que al perder electrones pasen a
configuraciones más estables).
Por lo tanto el elemento con menor energía de ionización es el potasio (Z=19). Además el
potasio al perder su único electrón de la capa más externa pasaría a tener la estructura del
Argón, que es muy estable, mientras que su vecino el calcio, que tiene estructura ns2 si
pierde un electrón tendría una estructura menos estable que la que tiene con el subnivel
lleno. El calcio precisamente lo que tiende es a perder, no uno, sino los dos electrones para
tener la configuración del Argón.
c) Puesto que la tendencia de todos los elementos es a tener la configuración electrónica
del gas noble más próximo, la tendencia de cada uno de los elementos en cuestión sería:
•
•
•
•
Flúor y cloro tienden a captar 1 electrón, convirtiéndose en los iones F− y Cl− con
la misma configuración electrónica del neón y argón respectivamente
Azufre tiende a captar 2 electrones, convirtiéndose en el ión S2−, con la misma
configuración electrónica del argón
Potasio a perder 1 electrón, convirtiéndose en el ión K+, con la misma
configuración electrónica del argón
Calcio a perder 2 electrones, convirtiéndose en el ión Ca2+, con la misma
configuración electrónica del argón
Ejemplo 7: E3A.S2006
La configuración electrónica de la capa de valencia de un elemento A es 3s2p5.
a) Justifique si se trata de un metal o un no metal.
b) Indique, razonadamente, un elemento que posea mayor potencial de ionización que A.
c) Indique, razonadamente, un elemento que posea menor potencial de ionización que A.
a) El elemento que en la última capa tiene configuración 3s2p5 corresponde a un halógeno
y al corresponder al nivel 3 se trataría del cloro. El cloro es un no metal típico por los
siguientes motivos:
•
•
La electronegatividad sirve para clasificar los elementos en metales o no metales,
según sean poco o muy electronegativos y el cloro tiene una electronegatividad
muy grande, porque esta muy a la derecha y arriba de la tabla periódica.
La tendencia del cloro es a ganar un electrón, convirtiéndose en el ión Cl− con la
3s2p6 configuración igual a la del argón.
b) El potencial de ionización es un concepto similar al de energía de ionización con la
diferencia de que en lugar de medir la energía necesaria para arrancar un electrón mide el
potencial (en voltios) necesario para arrancárselo.
Un elemento con mayor potencial o energía de ionización que el cloro por ejemplo es su
vecino argón, ya que al tratarse de un gas noble y tener una estructura muy estable es muy
difícil quitárselo porque supone desestabilizarlo. Otro ejemplo podía ser el flúor que está
por encima y al ser más pequeño mantiene más retenido a su electrón que en el caso del
cloro, que tiene mayor tamaño.
c) Con menor energía de ionización que el cloro, por ejemplo, tenemos al azufre o al
bromo, porque ambos tienen mayor tamaño. El azufre porque aunque es del mismo nivel,
está a su izquierda, y tiene 1 protón menos así que los electrones están menos retenidos. El
bromo porque es de un nivel mayor y por tanto tiene mayor tamaño y sus electrones están
menos retenidos.
En ambos cuestiones, se ha preferido escoger unos ejemplos de elementos cercanos al
cloro, en su mismo periodo y de su misma familia. Obviamente podríamos haber escogido
a cualquiera, por ejemplo al helio que es el que tienen mayor energía de ionización de
todos y al cesio que es el que la tiene mas pequeña.
6. VALENCIA.
La valencia es la capacidad de un elemento químico para combinarse, es decir, el número
de enlaces químicos que puede formar. Como veremos en el próximo tema, la valencia de
un ión es igual al número de electrones que gana o pierde y la valencia de un átomo en
general es igual número de electrones desapareados que tiene. Vamos a ver los elementos
del segundo periodo.
Li: 2s1
Be: 2s2
como la diferencia de energía entre dos subniveles del mismo nivel es muy
pequeña, el electrón puede saltar del s al p, dando lugar a 2 electrones
desapareados. En este, y en los demás casos similares, la inversión de energía
para hacer que el electrón salte se compensa con creces al formar dos enlaces.
B: 2s2p1
C: 2s2p2
N: 2s2p3
El nitrógeno no tiene subniveles vacíos dentro del mismo nivel, así que para
desaparear su electrón tendría que saltar de nivel y esa diferencia de energía
no se compensa con la formación de un enlace más.
P: 3s2p3d0
El fósforo, aunque es de la misma familia que el nitrógeno, está en el tercer
nivel y ya si tiene un subnivel d completamente vacío a donde puede saltar el
electrón s.
O: 2s2p4
Ninguno de los dos electrones apareados del oxígeno pueden desaparearse
porque no tiene un subnivel vacío en el segundo nivel. El oxígeno solo puede
tener valencia 2, pero eso no le ocurre al resto de su familia.
S: 3s2p4d0 El azufre, aunque es de la misma familia que el oxígeno, está en el tercer nivel
y, lo mismo que pasaba con el fósforo, ya si tiene un subnivel d
completamente vacío a donde puede saltar el electrón s.
F: 2s2p5
Cl:
3s2p5d0
Ejemplo 8: E1A.S2009
Considere el elemento cuya configuración es 1s2 2s2 2p6 3s2 3p4.
a) De qué elemento se trata?
b) Justifique el periodo y el grupo del sistema periódico a los que pertenece
c) Cual será la configuración de su ión más estable?
a) Para averiguar de qué elemento se trata no hay más que empezar a contar hasta llegar a
2+2+6+2+4=16 que son los electrones que tiene. Llegaríamos hasta el lugar que ocupa el
Azufre.
b) Está en el periodo n=3, como muestra en la configuración electrónica que es su última
capa, y al tener configuración s2p4 pertenece al grupo 16, del oxígeno, llamados anfígenos.
c) Como vemos, al azufre le faltan 2 electrones para tener la configuración del gas noble
más cercano, así que su tendencia es a captarlos convirtiéndose en el ión S2−.
7. IONES.
Algunos elementos tienden a obtener la estructura electrónica más estable, igual a la de los
gases nobles, ganando o perdiendo electrones hasta tener la misma configuración
electrónica del gas noble más cercano.
Aquellos elementos que tienen uno, dos o tres electrones más que un gas noble tienden a
perderlos para igualar su estructura electrónica, así:
• Los metales alcalinos con configuración en la última capa ns1 tienden a perder el
último electrón pasando así a iones M+ isoelectrónicos con el gas noble anterior.
• Los metales alcalino−térreos tienen en la última capa ns2 y por tanto su tendencia
es a perder dos electrones pasando a iones M2+.
• El Aluminio que tiene configuración 1s2 2s2 2p1 tiende a perder 3 electrones y se
convierte en el ión Al3+ isoelectrónico con el Helio.
Al contrario ocurre con los elementos a los que les falta uno o dos electrones para
completar la estructura de un gas noble, como es el caso de los halógenos que tienden a
ganar 1e− y de los anfígenos que tienden a ganar 2e−.
Aquí conviene hacer una aclaración importante: Los electrones no están en el aire, ni en
una caja. Los electrones están formando parte de los átomos. Dejando clara esta obviedad
puedes comprender que la tendencia a ganar o perder electrones de un elemento y
convertirse en ion no solo depende de él mismo, sino también del elemento con quien se
junte, ya que los que los electrones que un elemento pierda otro debe ganarlos y viceversa.
Así, si por ejemplo, el berilio frente al cloro cederá sus dos electrones convirtiéndose en
iones Be2+ y 2 Cl–, pero cuando el berilio se combina con hidrógeno lo hace compartiendo
electrones, aunque es verdad que el par de electrones del enlace esté más cerca del berilio
por tener mayor electronegatividad, pero sin llegar a formarse los iones.