Problemario 1 - prof.usb.ve.
Anuncio
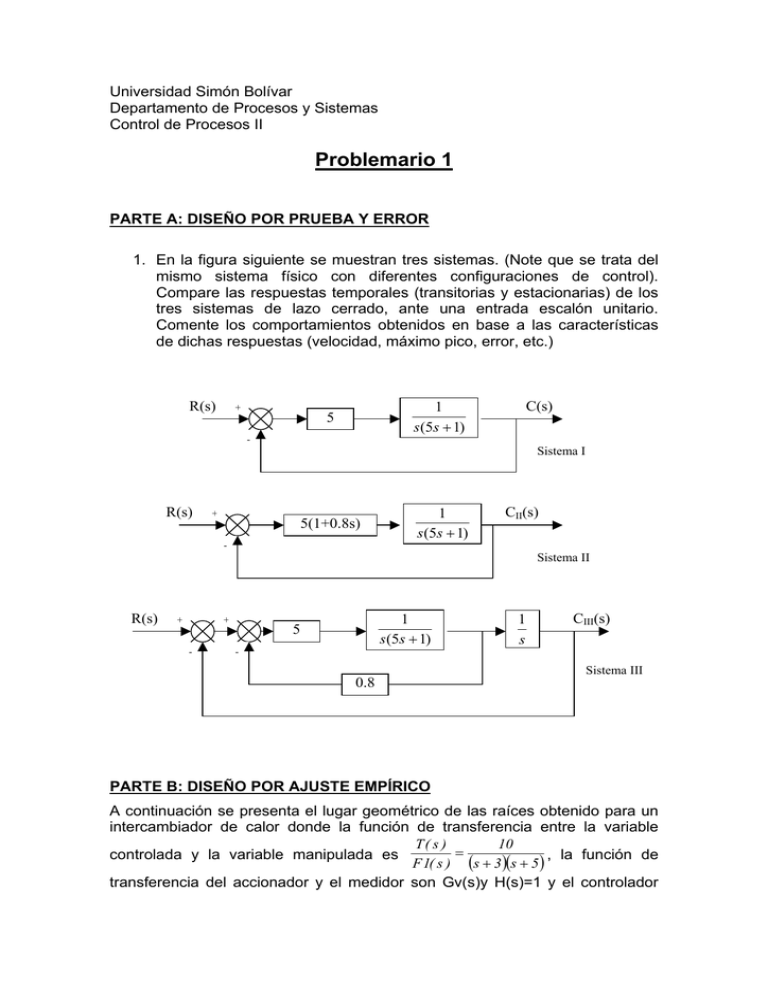
Universidad Simón Bolívar Departamento de Procesos y Sistemas Control de Procesos II Problemario 1 PARTE A: DISEÑO POR PRUEBA Y ERROR 1. En la figura siguiente se muestran tres sistemas. (Note que se trata del mismo sistema físico con diferentes configuraciones de control). Compare las respuestas temporales (transitorias y estacionarias) de los tres sistemas de lazo cerrado, ante una entrada escalón unitario. Comente los comportamientos obtenidos en base a las características de dichas respuestas (velocidad, máximo pico, error, etc.) R(s) + C(s) 1 s (5s + 1) 5 - Sistema I R(s) + 5(1+0.8s) 1 s (5s + 1) CII(s) - Sistema II R(s) + + - 1 s (5s + 1) 5 1 s CIII(s) - Sistema III 0.8 PARTE B: DISEÑO POR AJUSTE EMPÍRICO A continuación se presenta el lugar geométrico de las raíces obtenido para un intercambiador de calor donde la función de transferencia entre la variable T( s ) 10 = controlada y la variable manipulada es , la función de F 1( s ) (s + 3)(s + 5 ) transferencia del accionador y el medidor son Gv(s)y H(s)=1 y el controlador tiene Gc(s)=1. Además, se presenta la curva de respuesta (T*(t)) del sistema a lazo abierto al ser perturbado con un escalón unitario en F1(s). Root Locus 2.5 2 1.5 1 0.5 si x A g a m I 0 -0.5 -1 -1.5 -2 -2.5 -5 -4.5 -4 -3.5 -3 -2.5 Real Axis Step Response 0.7 0.6 0.5 ar ut ar e p m e T 0.4 0.3 0.2 0.1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 Time (sec) 1. ¿Cuál será la ganancia de controlador proporcional para que la respuesta del sistema a lazo cerrado presente un error del 10% ante un escalón de referencia? Para ese controlador, ¿cómo será el comportamiento del sistema en cuanto a estabilidad absoluta, relativa y velocidad de respuesta? 2. Calcule la ganancia óptima del controlador proporcional utilizando el método de sintonización que pueda aplicarse con la información suministrada sobre el sistema. Para ese controlador, ¿cómo será el comportamiento del sistema en cuanto a precisión, estabilidad absoluta, relativa y velocidad de respuesta ante un escalón de referencia? 3. Repita el punto 2, pero ahora, sintonice un controlador que garantice error finito ante una entrada rampa. Para analizar el comportamiento del sistema a lazo cerrado realice el LGR del sistema con el nuevo controlador. PARTE C: DISEÑO POR LGR Los siguientes problemas se refieren al diseño de compensadores para sistemas que han de ser controlados en retroalimentación simple, y que tienen la función de lazo abierto GH(s) dada en cada caso. Para cada conjunto de especificaciones dadas Ud. debe: a.) Dibujar con MatLab el diagrama del lugar de las raíces b.) Explicar qué tipo de compensador usará y por qué (si se podría usar indistintamente un compensador en adelanto o uno en atraso por ejemplo) para cumplir los requerimientos del diseño. c.) Determinar la función de transferencia del compensador Gc(s) que Ud. propone. d.) Realizar la verificación del diseño obteniendo (también con MatLab) con el diagrama de LGR del sistema compensado. e.) Puntualizar algunas conclusiones sobre el diseño, comparando la respuesta del sistema original y la del sistema compensado (utilice otras herramientas de MatLab como la respuesta transitoria...) PROBLEMAS 10(s + 500) , diseñe un compensador (s + 1)(s + 60) para que los polos dominantes (lazo cerrado) del sistema compensado se encuentren en s=-3±5j. 1.06 2) Considere el sistema con GH(s) = . Se desea incrementar el s(s + 1)(s + 2) coeficiente de error de velocidad Kv a aproximadamente 1 seg-1 sin modificar apreciablemente la ubicación de los polos dominantes de lazo cerrado. 10 3) Dada GH(s) = , diseñar un compensador de manera que el s(s + 3)(s + 10) coeficiente de error de velocidad Kv sea igual a 0.1 seg-1 y los polos dominantes de lazo cerrado estén situados en s = −2 ± 2 3 j . 1) Dado un sistema con: GH(s) = 4) Dado un sistema cuya FTLA es GH(s) = K , diseñar un compensador s2 que estabilice el sistema y que cumpla los siguientes requerimientos: los polos dominantes tienen ξ = 0,5 y ts(2%) =2 seg . Encuentre e (t) ante una entrada escalón para el sistema sin compensar y el sistema compensado. 110 5) Dado GH(s) = . Determinar un compensador de modo que los s(s + 5) polos dominantes de lazo cerrado tengan ξ = 0,6 ; Wn= 23 rad/seg. La adición del compensador no debe afectar las características del sistema en estado estacionario. K * (s + 16 ) 6) Se tiene GH(s) = s(s + 7)(s + 25)(s + 33) Para este sistema operando en lazo cerrado: (a) Encontrar el valor de K que dará un Mp= 15% ante una entrada escalón unitario. Calcule Kv y el correspondiente ts(2%). (b) Diseñar un compensador en serie que producirá el mismo Mp que el apartado (a), pero con ts (5%)= 0,32 seg, para una entrada escalón unitario. Suponga que K se mantiene constante en el valor calculado en (a) ¿Cuál es el valor de Kv para este compensador? 7) Diseñe un compensador que no incluya cambios apreciables en la localización de los polos del sistema de lazo cerrado que corresponde a la función de lazo abierto dada a continuación, pero que logre que la constante de error de velocidad sea 30s-1. 15 GH(s) = (s + 5)(3s + 300) 8) Se desea compensar el sistema térmico de función de transferencia a s+8 lazo abierto GH(s)= s(s + 3)(s + 5) a) Diseñe un controlador que garantice tss2%<4 y Mp=0 (3 ptos) b) Diseñe un compensador que permita obtener tss2%<2 y Mp<25%