II - Actualidad Empresarial
Anuncio

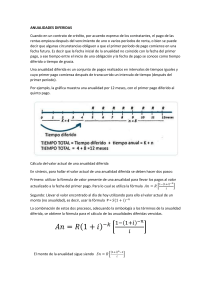
II Área Indicadores Económico-Financieros II Contenido INFORME FINANCIERO Matemáticas Financieras: Anualidades II-1 Variación de los Indicadores de Precios de la Economía II-2 II-2 INDICADORES ECONÓMICO- Cotizaciones Internacionales FINANCIEROS Tasas de Interés Promedio del Sistema Financiero II-2 II-4 Tipo de cambio/Devaluación/Tasa Legal Laboral/CTS Solución: Ficha Técnica Autora : Mariela Melissa Ricra Milla Realizando el diagrama de flujo de caja para visualizar los pagos: Título : Matemáticas financieras: Anualidades R Fuente : Actualidad Empresarial Nº 281 - Segunda Quincena de Junio 2013 R 1. Definición R R R • • • 0 1 2 • • • 3 12 Los datos son: Una anualidad se define como un conjunto de pagos en serie que cumplen las siguientes condiciones: R= S/. 1,000 N=12 I= 1.3% mensual capitalizable al mes • Todos los depósitos son del mismo valor, y son cancelados en iguales intervalos de tiempo. • Todas las cuotas están afectadas por la misma tasa de interés • El número de pagos es igual al número de periodos. Cuando se cumplan los 12 periodos mensuales se cumple el año; por lo cual la sustitución de la ecuación queda de la siguiente forma: M=R 2. Clasificación Criterio Tiempo (fecha de inicio y fin) Tipo Descripción Ciertas Anualidad cierta: Sus fechas son fijas y se estipulan de antemano. Contingentes Anualidad contingente: La fecha del primer pago, la fecha del último pago, o ambas no se fijan de antemano. Generales Anualidad general: Son aquellas que el periodo de pago no coincide con el periodo de capitalización. Simples Anualidad simple: Cuando el periodo de pago coincide con el de capitalización de los intereses. Vencidas Anualidad vencida: Son aquellas en que los pagos se efectúan a su vencimiento, es decir, al final de cada periodo. Anticipadas Los pagos se efectúan al principio de cada periodo. Inmediatas La realización de los cobros o pagos tiene lugar en el periodo inmediatamente siguiente a la formalización del trato. Diferidas La realización de los cobros o pagos se hace tiempo después de la formalización del trato (se pospone). Intereses Pagos Iniciación 3. Casos prácticos a) Un trabajador deposita S/.1,000 en una cuenta de ahorros al inicio de cada mes; si dicha cuenta paga 1.3% de interés mensual capitalizable al mes, ¿cuánto habrá ahorrado al cabo de un año? N° 281 Informe Financiero Matemáticas financieras: Anualidades Segunda Quincena - Junio 2013 M=1,000 (1+i)n-1 i (1+0.013)12-1 0.013 (1+i) (1+0.013)=13,063.94 b) Un grupo de jóvenes quieren formar una banda de rock, para ello, necesitan comprar una batería que cuesta $8,000.00 por el momento no tienen dinero, y le piden a la tienda que se las venda a crédito, el gerente les explica que no puede concederles el crédito porque no puede comprobar ingresos, entonces les propone que al final de cada mes entreguen una cantidad a la tienda, para que se vaya acumulando y dentro de cinco meses cuando completen el monto, les entrega la batería. ¿De cuánto tendría que ser el pago si el gerente de la tienda ofrece un interés efectivo mensual de 1%? Solución: Datos: n=5 i= 1% = 0.01 M = $8,000 Fórmula para calcular la renta de la anualidad: R= R= Mi (1+i)n -1 8,000 * 0.01 (1 + 0.01)5-1 = 1,568.32 Entonces el grupo pagará la cantidad de $1,568.32 mensuales para tener su batería en cinco meses. Actualidad Empresarial II-1