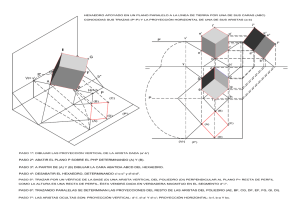
Engranes Rectos
Anuncio

t 210 ENGRANAJES. Un e n g r a n e e s e l e l e m e n t o básico de l o s er.gr;-a j e s . Los e i c r r e s s o n p i e z a s c i l i n d r i c a s de m a t e r i a l sólido r e - r a n u r ü c i m ^ t r i c a s a s u a l r e d e d o r . L a s r a n u r a s que f o r m a r l o s d i e n t e s e v i t a n l e s — r e s b a l a m i e n t o s e n u n a transmisión. Para e v i t a r g o l p e t e e y; r u i d o s e x c e s i v o s e n s u f u n c i o n a m i e n t o , e s n e c e s a r i o diseñarles yj c c s - t r u i r l o s l l e n a n d o t o d o s l o s r e q u i s i t o s e s t a b l e c i d o s r a r a t a l objetivo. - E l e n g r a n e e s l a p a r t e f u n d a m e n t a l de l o s e — r a n a j e s que sor. -c o m b i n a c i o n e s d e r u e d a s d e n t a d a s u t i l i z a d a s p a r a t r a n s m i t i r un. m o v i m i e n t o g i r a t o r i o de un e j e a o t r o . L o s e n g r a n a j e s se d i v i d e n e n g r u p o s y se d e s i g n a n p e r l a o c s i ción q u e t i e n e n l o s d i e n t e s r e s p e c t o a l e j e de r o t a o i f n i a l e r . — g r a n a j e . E n t r e l o s mas comunes tenemos l o s s i g u i e n t e s : 1. 2. 3. 4. Engranajes rectos E n g r a n a j e s cónicos Engranajes h e l i c o i d a l e s E n g r a n a j e s de t o r n i l l o siríin y rueda Etc. cerrada, Jjos p r i m e r o s , e s a e c i r i o s e n g r a n a j e s r e c t o s , se eiL _-nn néctar árboles c u y o s e j e s s o n p a r a l e l e s . r jai.* _ w L o s e n g r a n a j e s cónicos, l o s d i e n t e s s e r t a l l a d o s serré una süper' f i c i e cónica, s e e m p l e a n e n t r e e j e s cuyas líneas ce r e n t r o se -cortan. L o s e n g r a n a j e s h e l i c o i d a l e s t i e n e n sus d i e n t e s t a l l a d o s a c i e r t o ángulo c o n e l e j e d e rotación. L o s e n g r a n a j e s de t o r n i l l o siríin, c o n s i s t e ¿e una rueda t a l l a d a c o n d i e n t e h e l i c o i d a l , l a c u a l e s a c c i o n a d a p o r un h u s i l l o o t o r nillo sinfin. Los e n g r a n a j e s ' de cheurón, t i e n e n d i e n t a s h e l i c o i d a l e s d o b l e s , v s o n e m p l e a d o s c u a n d o s e n e c e s i t a n v e l o r i d a d e s y r e l a c i o n e s ce transmisión e l e v a d a s . E n g r a n a j e s de e s p i r a l , t i e n e n d i e n t e s t a l l a d o s sobre s j p e r f i c i e cónica y Curvados" e n f o r m a de e s p i r a l , s o n u t i l i z a d o s o r . i n c i p s l m e n t e e n l a transmisión a l e j e t r a s e r o de l o s automóviles. En l a formación d e l p e r f i l s i s t e m a s de u s o g e n e r a l : de l o s d i e n t a s de e n g r a n a - e s , hav dos c a) Envolvente n o r m a l c u y o -<£ de presión es 5e 1 4 2 ' b) Envolvente stub cuyo El prjmero _<^; de presión es r e 2 0 c e s de m á s u s o . Atendiendo a l o a n t e r i o r , engrane. es n e c e s a r i o conocer l a s c a r n e s ce un- En l a h o j a s i g u i e n t e s e p r e s e n t a un e n g r a n e , m o s t r a n d o sus p a r t e s principales. 211 Df De D 0 p' p S B E T W W c C N Np Nc L M = = = = = = = = = = = = = = = = = Diámetro de f o n d o Diámetro de c l a r o Diámetro p r i m i t i v o o d e p a s o Diámetro e x t e r i o r Paso c i r c u l a r Paso d i a m e t r a l S u p l e m e n t o , c a b e z a d e d i e n t e o addendum P i e d e l d i e n t e , base o dedendum E s p e s o r d e l d i e n t e e n e l círculo p r i m i t i v o Espacio entre dientes Profundidad t o t a l d e l diente P r o f u n d i d a d útil d e l d i e n t e C l a r o de e n g r a n a j e Distancia entre centros Número de d i e n t e s d e l e n g r a n e Número de d i e n t e s d e l piñón Número de d i e n t e s de l a c r e m a l l e r a L o n g i t u d de u n a c r e m a l l e r a Módulo p a r a e n g r a n e s métricos 212 E x i s t e n d o s s i t e m a s p a r a e l cálculo de l a s !ii=¡er.siones y t a l l a d o de l o s e n g r a n e s . 1. - Por e l paso d i a m e t r a l ( d i a m e t r a l P i t c h i sistema i n g l e s j 2. ^ P o r e l m ó d u l o , s i s t e m a m é t r i c o . i E l p r i m e r o se u s a e n l o s p a i s e s d e h a b l a ir.¡ilesa, y e l segunde en l o s p a i s e S d o n d e e l s i s t e m a m é t r i c o t i e r J ; su n a y o r arlicaciér. En n u e s t r o p a i s , p o r c i r c u n s t a n c i a s e x i s t e n t e s d e n t r o de l a i n d u s t r i a , e s n e c e s a r i o e m p l e a r ambos. H a c i e n d o c a s o a l o e s t a b l e c i d o , l a s m e d i c a de l o n g i t u d t a r a l o s e n g r a n e s de p a s o d i a m e t r a l , s i e m p r e estará -.1 dadas en p u l g a d a s , i p a r a l o s e n g r a n e s de módulo, s u s d i m e n s i o n e s están dadas en nilí metros. S i e n d o e l p a s o d i a m e t r a l y e l m ó d u l o , f a c t o r e s rn¡r/ i m p o r t a n t e s p a r a e l cálculo, diseño y t a l l a d o d e l o s engranes en uno y o t r o s i s t e m a , a continuación se da u n a definicié -. y explicación d e l tema q u e n o s o c u p a . Definición: Paso d i a m e t r a l e s u n a relación e n t r e e l numere de d i e n t e s y e l diámetro p r i m i t i v o c u a n d o se e x p r e s a en p u l g a d a s - o sea e l núrter o de d i e n t e s ' p o r p u l g a d a e n e l diámetro Primitúir;. Ejemplo. J S i u n e n g r a n e t i e n e u n d i á m e t r o p r i m i t i v o de S** y 24 d i e n t e s , -tendrá 4 d i e n t e s p o r c a d a ^ u l g ^ d a e n su diámetro p r i m i t i v o p o r que 24/6 = 4, ésto e s un e n g r a n e d e pase d i a m e t r a l 4. E s t e er.gra_ ne sólo engranará c o n o t r o s de p a s o 4. t 213 ESQUEMA REPRESENTATIVO PASO DIAMETRAL Ñ = 24 d i e n t e s D = 6" (DIAMETRAL P I T C H ) . 4 Dientes p o r pulgada e n s u diámetro p r i m i t i v o Un e n g r a n e d e p a s o d i a m e t r a l 6, sólo engranará c o n o t r o s de p a s o d i a m e t r a l 6; Un e n g r a n e d e p a s o d i a m e t r a l 8, sólo engranará c o n o t r o s d e p a s o 8, y así s u c e s i v a m e n t e , n o s e d e b e n a c o p l a r e n g r a — nes de d i f e r e n t e paso d i a m e t r a l . Definición. MODULO.- Es l a relación d e l diámetro p r i m i t i v o a l número de d i e n t e s e x p r e s a d o e n m i l í m e t r o s , o s e a q u e e l módulo r e p r e s e n t a u n a l o n g i t u d q u e e s e l número d e milímetros d e l diámetro p r i m i t i v o por d i e n t e . E j e m p l o . Cuando u n e n g r a n e t i e n e 54 mm d e diámetro p r i m i t i v o y 18 d i e n t e s , s u módulo e s 3, p o r q u e 5 4 / 1 8 = 3 mm. de diámetro p r i mitivo por diente. E s t e e n g r a n e s o l o engranará c o n o t r a s d e módulo 3. Ruedas d e d i f e r e n t e módulo n o d e b e n a c o p l a r s e . FORMULAS PARA CALCULAR LAS DIMENSIONES DE ENGRANES RECTOS DE ENVOLVENTE, POR EL SISTEMA PASO DIAMETRAL. NO. 1 2 3 ,4 5 6 PARA HALLAR Paso d i a m e t r a l • ii Paso •i ii ii circular ii Diámetro p r i m i t i v o o de - CONOCIENDO Paso circular ti •i e n t r e e l paso Paso d i a m e t r a l Diámetro p r i m i t i vo y núm. de d i e n tes Número de d i e n t e s y paso d i a m e t r a l circu P = IT P' Núm. de d i e n t e s y diámetro e x t e r i o r entre e l P N D D i v i d i r e l núm. de d i e n t e s m á s 2 e n t r e e l diámetro e x t e r i o r P . N +2 Sí Dividir tral Pi 3.1416 e n t r e e l p a s o d i a m e 4- M u l t i p l i c a r e l diámetro p r i m i t i v o p o r 3.1416 y d i v i d i r e l p r o d u c t o e n t r e e l número de d i e n t e s / d i v i d i r e l núm. de d i e n t e s e n t r e e l / paso d i a m e t r a l P D i _ * P D TT N N P \ ii Número d e d i e n t e s ii Distancia entre 2 centros p a s o Diámetro y 9 3.1416, D i v i d i r e l núm. de d i e n t e s diámetro p r i m i t i v o y 8 Dividir lar FORMULA Núm. de d i e n t e s y diámetro p r i m i t i vo p a s o 7 REGLA c i r c u l a r exterior suplemento Núm. de d i e n t e s de l o s d o s e n g r a nes y e l paso d i a metral e l número de d i e n t e s — e l paso c i r c u l a r y d i v i d i r e l p r o d u c t o e n t r e 3.1416 D Restar 2 veces e l diámetro e x t e r i o r D - 0-2 S M u l t i p l i c a r por s u p l e m e n t o del — N P' TT Sumar e l núm. de d i e n t e s de l o s d o s e n g r a n e s y d i v i d i r l a suma e n t r e 2- C veces e l paso d i a m e t r a l N + Np 2P No. PARA HALLAR 1Q Suplemento 11 Base 12 Claro PasO it ii diametral ti n m 13 14 15 16 17 18 19 20 Profundidad t o t a l del diente ti H ti ii P r o f u n d i d a d -útil de d i e n t e ¡i •i Diámetro rior ii ii ti extett REGLA CONOCIENDO •i Paso it circular FORMULA D i v i d i r e l número u n o e n t r e diametral e l paso D i v i d i r e l número u n o e n t r e diametral e l paso D i v i d i r e l número c o n s t a n t e e n t r e e l paso d i a m e t r a l 0.157 - D i v i d i r e l número c o n s t a n t e e n t r e e l paso d i a m e t r a l 2.157 - S 1 p B 1 p C 0^157 P W 2.157 P M u l t i p l i c a r e l número c o n s t a n t e 2.157 p o r e l p a s o c i r c u l a r y d i v i d i r e l p r o d u c t o e n t r e 3.1416 W S u p l e m e n t o y cía ro M u l t i p l i c a r por 2 e l suplemento y a l p r o d u c t o sumar e l c l a r o W = 2 S + c Paso D i v i d i r e l número 2 e n t r e diametral W diametral e l paso - Suplemento Multiplicar plemento Paso M u l t i p l i c a r e l número 2 p o r e l p a s o c i r c u l a r y d i v i d i r e l producto e n t r e 3.1416. circular e l número 2 p o r e l s u - número de d i e n t e s y paso d i a m e t r a l D i v i d i r e l número d e d i e n t e s / e n t r e e l paso d i a m e t r a l Número de d i e n t e s y paso c i r c u l a r Sumar e l número de d i e n t e s m á s 2, y m u l t i p l i c a r p o r e l paso c i r c u l a r , \ e l p r o d u c t o d i v i d i r l o e n t r e 3.1416 2.157 P' TT w w 2 P = 2 S 2 P' TT N + 2 P m á s 2, à (N+2) P ' TT PARA HALLAR No. CONOCIENDO REGLA e x t e — Diámetro p r i m i t i v o y suplemento 21 Diámetro rior 22 Diámetro de f o nP r o f u n d i d a d t o t a l y diámetro e x t e — do • rior Se m u l t i p l i c a p o r 2 l a p r o f u n d i d a d t o t a l y e l p r o d u c t o se r e s t a d e l — diámetro e x t e r i o r Df Diámetro de claro M u l t i p l i c a r 2 p o r e l suplemento, y e l p r o d u c t o se r e s t a d e l diámetro primitivo De = D - 2 S l y ~ primitivo M u l t i p l i c a r e l paso d i a m e t r a l p o r e l diámetro p r i m i t i v o N = PD Diámetro p r i m i t i v o y paso c i r c u l a r M u l t i p l i c a r .3.1416 p o r e l diámetrop r i m i t i v o y d i v i d i ó , e i t/iioducto c u t r e e l paso c i r c u l a r »* _ ¿i • — D i v i d i r e l número c o n s t a n t e entr'e e l p a s o d i a m e t r a l E = 23 24 25 26 27 28 — Número de d i e n tes ii ii Espesor d e l — d i e n t e y espacio entre dien tes ti ti L o n g i t u d de -una c r e m a l l e r a Diámetro p r i m i t i v o y suplemento a Paso 4 i diámetro m e t r a Paso d i a m e t r a l Paso A l diámetro p r i m i t i v o ces e l s u p l e m e n t o FORMULA sumar d o s v e - D i v i d i r e l paso c i r c u l a r circular 1.5708- entre 2 M u l t i p l i c a r 3.1416 p o r e l número de d i e n t e s d e l a c r e m a l l e r a , e l — p r o d u c t o se d i v i d e e n t r e e l p a s o diametral Número d e d i e n t e s de l a cremalléray paso d i a m e t r a l i D + 2 S = 0 - 2 W P' _ 1.5708 P T E = L = P' 2 = NC TT P _ 217 Aplicación de l a s fórmulas p a r a un e n g r a n e i n e p t o p o r e l s i s t e m a Paso D i a m e t r a l . Ejemplo: C a l c u l a r l a s d i m e n s i o n e s de u n e n g r a n e t r o e x t e r i o r y e l número de d i e n t e s . r e c t o , conocidos e l di&ae Datos: 0 = 1.750" N = 12 N + 2 ^ 1 2 + 2 Sr 1.750 F D w = • P W = - f - = S = -±- = P 14 1.750 _ = 1.500" 8 - °' -i- = 8 °- 2 5 1 2 5 °" " Df = JÍ - 2 W = 1.750 - 2 x 0.2696 = 1.750 - 0.5392 = 1.2108" De = D - 25 = 1.500 - 2 x 0.125 = 1.500 - 0.250 = 1.250" 218 ESQUEMA REPRESENTATIVO DE MODULO Fórmulas : Módulo = 3 mm p o r d i e n t e e n e l diámetro Un e n g r a n e c o n módulo 3 y 4 0 , d i e n t e s , de diámetro primitivo. Primitivo tendrá 3 x 40 = 120 mm. FORMULA PARA CALCULAR LAS DIMENSIONES DE ENGRANES RECTOR DE ENVOLVENTE POR EL SISTEMA MODULO (METRICOS) No. 1 2 3 4 PARA HALLAR Paso Modulo •i tt Paso circular 5 6 Diámetro mitivo pri- 7 8 •i ti 9 a CONOCIENDO circular | REGLA Dividir e l paso c i r c u l a r FORMULA entre Diámetro p r i m i t i v o y número de -dientes D i v i d i r diámetro p r i m i t i v o m e r o de d i e n t e s Diámetro e x t e r i o r y número d e d i e n tes d i v i d i r e l diámetro e x t e r i o r e l número de d i e n t e s m á s 2 Módulo Multiplicar Diámetro p r i m i t i v o y número de -dientes M u l t i p l i c a r 3.1416 p o r e l diámetro p r i m i t i v o y d i v i d i r e l p r o d u c t o en t r e e l número de d i e n t e s Número de d i e n t e s y módulo Multiplicar de d i e n t e s Número de d i e n t e s y paso c i r c u l a r M u l t i p l i c a r número d e d i e n t e s p o r paso c i r c u l a r y d i v i d i r e l p r o d u c t o e n t r e 3.1416 Diámetro e x t e r i o r y número d e d i e n tes M u l t i p l i c a r e l número de d i e n t e s p o r e l diámetro e x t e r i o r y d i v i d i r e l p r o d u c t o e n t r e e l número d e d i e n t e s m á s 2. Diámetro y módulo M u l t i p l i c a r p o r 2 e l módulo y r e s t a r e l p r o d u c t o d e l diámetro e x t e rior exterior P' 3.1416 M TT e n t r e núM entre - 3.1416 p o r e l módulo e l módulo p o r e l número ' D N 9 N + 2 M P' = TT M P P D N D = M N D = D = N P' TT • N ÇS N + 2 D = g - 2 M : NO .• PARA HALLAR io.. Diámetro t M u l t i p l i c a r e l módulo p o r e l número de d i e n t e s m á s d o s 0 = M i Diámetro p r i m i t i v o y módulo . M u l t i p l i c a r p o r 2 e l módulo y sumar e l p r o d u c t o a l diámetro p r i m i t i v o V Número d e d i e n t e s y paso c i r c u l a r m u l t i p l i c a ) ? e l número d e d i e n t e s — más 2 p o r e l p a s o c i r c u l a r y d i v i — d i r e l p r o d u c t o e n t r e 3.1416 0 Diámetro p r i m i t i v o y paso c i r c u l a r M u l t i p l i c a r p o r 2 ex paso c i r c u l e n d i v i d i r e l p r o d u c t o e n t r e 3.1416 s u mar e l c o c i e n t e a l diámetro p r i m i t a vo Diámetro p r i m i t i v o y módulo D i v i d i r e l diámetro p r i m i t i v o e l módulo Diámetro p r i m i t i vo y paso c i r c u — lar M u l t i p l i c a r 3.1416 p o r e l diámetro p r i m i t i v o y d i v i d i r e l producto e n t r e e l paso c i r c u l a r E s p e s o r d e l -diente, y espacio entre dien tes Paso Dividir Suplemento y — base Módulo E l s u p l e m e n t o ( c a b e z a de d i e n t e ) e s i g u a l a l a base (pie. de diente.) ye s t o e s i g u a l ál módulo S = B = M Paso circular Dividir 3.1416 entre S = B - ' Paso circular D i v i d i r e l paso c i r c u l a r número v e i n t e entre e l - C = P-' •i H 12 . 11 13 i n I I 14 • Número de d i e n . t e s ,•'• 17 it n H 18'. 19 FORMULA Número d e d i e n t e s y módulo il T 6 REGLA exte- . rr i o r 15 CONOCIENDO Claró d e e n g r a naje.. .... circular e l paso c i r c u l a r e l paso c i r c u l a r entre entre 2 D + 2 M -. N (N+2) P* 7T 2P ' — ïï D + 0 N (N + 2) m. D M D P' TT 1 E = P 2 - P U 20 No. PARA HALLAR CONOCIENDO. C = 0.157 M Profundidad t o — j t a l y diámetro + exterior M u l t i p l i c a r por 2 l aprofundidad t o t a l y restar e lproducto a l diámetro exterior Df Módulo M u l t i p l i c a r e n número c o n s t a n t e 2.157 p o r e l módulo W = 2.157 M Paso M u l t i p l i c a r e l número c o n s t a n t e 0.68666 por. e l p a s o c i r c u l a r W = 0.68666P' C l a r o de e n g r a naje Módulo. 21 Diámetro d e fondo 22 23 24 25 Profundidad t o tal- d e l diente M it P r o f u n d i d a d -útil d e l d i e n t e •i ii FORMULA M u l t i p l i c a r e l número c o n s t a n t e 0.157 p o r e l módulo 20 — REGLA X, circular Módulo Multiplicar Paso M u l t i p l i c a r dos p o r e l paso c i r c u lar y d i v i d i r e l producto entre — 3.1416 circular d o s p o r e l módulo W = SS - 2W = 2 M 2 P' 22c Aplicación de l a s fórmula p a r a c a l c u l a r l a s d i m e n s i o n e s de un -e n g r a n e r e c t o p o r e l s i s t e m a d e l Módulo. Ejemplo: C a l c u l a r l a s p a r t e s de u n e n g r a n e número d e d i e n t o s y e l m ó d u l o . métrico r e c t o , c o n o c i e n d o e l - - Datos: ¡ N M i = 50 = 3 P' D = TT x M = 3. 1416 x 3 = 9.4248 = MN = 3 < 50 = 150 Sí = M W = 2.157 M W = .2 M = 2 x 3 = 6 (N + 2) = 3 ( 5 0 + 2) = 3 x 52 •= 156 - 2.157 x 3 = 6 . 4 7 1 D f = fif - 2 W = 156 - 2 x 6 1 4 7 1 = 156 - 12.942 • 1 4 3 . 0 5 8 C = 0.157 M = 0.157 x 3 = 0 . 4 7 1 _ _ _ _ P* ~~2 9.4248 ~ . = 4.7124 2 S = B = M = 3 N o t a . " L o s r e s u l t a d o s están e n m i l í m e t r o s . Por e j e m p l o : C a l c u l a r l o s d a t o s n e c e s a r i o s p a r a e l t a l l a d o de u n e n g r a n e q u e t i e n e u n módulo 2 c o n 40 d i e n t e s : D = N M = 2 x 4 0 = 8 0 m m 0 = (N f~2^\M = P' = E (40+ 2)2 = 4 2 x 2 = 84 mm M = 2 x 3.14 = 6.28 mm c = P' = 6.28 4 3.14 mm 2 2 / E S..14 0.314 = 10 10 W = + 2M = 10 3 , 1 4 10 + 2 x 2 = 0.314 + 4 = 4.314 mm 223 J u e g o de c o r t a d o r e s o f r e s a s p a r a so d i a m e t r a l . . Cortador No. 1 C o r t a de cremallera. M it ti 2 ti tt ti 3 ii n 4 " ii tt 5 ii 6 " H H 7 ii ti 8 II II II M II II 135 tallar engranajes envolventes para cada pa- dientes a la 55 35 26 21 17 14 12 " ti 134 •i 54 ii 34 tt 25 n .20 ti 16 ii 13 E s t a s e r i e de c o r t a d o r e s g e n e — raímente s o n l o s mas u s u a l e s , 8 para c a d a p a s o d i a m e t r a l . Como l o s que a p a r e c e n en l a f Lgura siguiente: Elección d e l c o r t a d o r f a r a s a r un e n g r a n e . Ejemplo. :' fre- Se d e s e a t a l l a r un e n g r a n e de 24 d i e n t e s p a s o d i a m e t r a l 4. - En l a t a b l a a n t e r i o r , L e o b s e r v a que e l c o r t a d o r No. 5, p u e d e c o r t a r de 21 a 25 d i e n t e s ; p o r lo tanto, e l cortador s e l e c c i o nado, tendrá l a s s i g u i e n t e s ca_ racterísticas. No. 5 - 4 Dp - 21 To 25 TD E n donde: 5 = Nogo. 4 Dp= de c o r t a d o r en e l jue_ Paso d i a m e t r a l 21 To 25 TD J u e g o de c o r t a d o r e s paso d i a m e t r a l . 4. - P a r a t a l l a r de a 25 d i e n t e s . 21 de E n forma s i m i l a r a l ejemplo a n t e r i o r , s e determina e l c o r t a d o r p a r a e l s i s t e ma que e m p l e a e l m ó d u l o . En l a página s i g u i e n t e s e dan t a b l a s de e s t o s c o r t a dores . E x i s t e ura s e r i e de c o r t a d o r e s p a r a c a d j i j p a s o d i a m e t r a l c o n m e d i o s números, c u a n do e s n e c e s a r i o una mayor perfección y e x a c t i t u d en l o s d i e n t e s de l o s e n g r a najes. A continuación s e p r o p o r c i o n a Cortador ti ii ii ii ti ii No. •i ii tt •t ti ti i 2 3 4 5 6 7 1/2 c o r t a de 80 1/2 " " 42 1 /2 30 23 1/2 19 1/2 " " 1/2 15 1 /2 13 No s e r e c o m i e n d a t a l l a r l a m i e n t o en l a r a i z . dicha tabla a 134 d i e n t e s w / ' a 54 ii a 34 tt a 25 tt 20 a ti a 16 ti e n g r a n e s m e n o r e s de 12 d i e n t e s , p u e s s u f r e n estrangu- 224 T a b l a de c o r t a d o r e s MODULO. p a r a e n g r a n e s métricos p o r e l s i s t e m a de — P a r a m ó d u l o s m e n o r e s de 10 Cortador No. •i II M II • « II II II II •1 II II ti 1 2 3 4 5 6 7 8 corta ii . •i ti M II II 12 14 17 21 a a a a a 35 a 55 a 135 a 13 d i e n t e s -•i 16 • 20 •i 25 •i .34 54 134 la cremallera IIII P a r a m ó d u l o s m a y o r e s de 1 0 , e s n e c e s a r i o u t i l i z a r una s e r i e de 15 c o r t a d o r e s p o r c a d a módulo, ésto e s d e b i d o a l a i m p o r t a n c i a de l a c u r v a t u r a de l o s d i e n t e s de l o s e n g r a n e s . P a r a m ó d u l o s m a y o r e s d e 10 Cortador If •1 ti •1 II II tl II * II II tl tl •1 No. 1 II 1 II 2 II 2 II 3 II 3 II 4 II 4 II 5 tl 5 II 6 II 6 II 7 II 7 It 8 c o r t a 12 •1 13 II 14. .11 15. 1/2 II < 17 n ' 19 1/2 ii 21' ii ,23 1/2 it r 26 ti 30 1/2 it 35 ti 42' 1/2 tt "55 •i 80 1/2 ii 135 dientes It 1/2 ; r •1 tt a: 16 tl a 18 tt a 20 tt 22 II a 25 II a 29 II a 34 II a 41 II a 54 •» a .79 II a 134 a la cremallera T a b l a de p a s o s d i a m e t r a l e s -Pasos Diametráje**Numero- y módulos mas Módulos . * Número 1 3.2 .0.5 1 1/2 i 4 7 . 0.75 2 1*6 ; 1 3 18 •• '1.25 . 4 '-2CÍ $ 1.5 1.75 5 24 2 6 30 2.25 7 8 ••*•«- 2.5 9 . - 2.75^ .3 í 10 3.25 3.5 3.75 4 4.25 4.5 4.75 5 5.25 5.5 5 6.5 7 7.5 8 8.5 9 9.5 10 11 12 13 14 15 16 18 20 22 usuales.