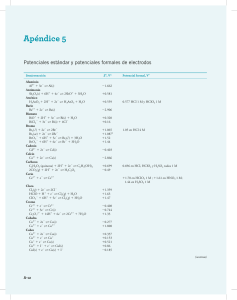
πε πε πε - U

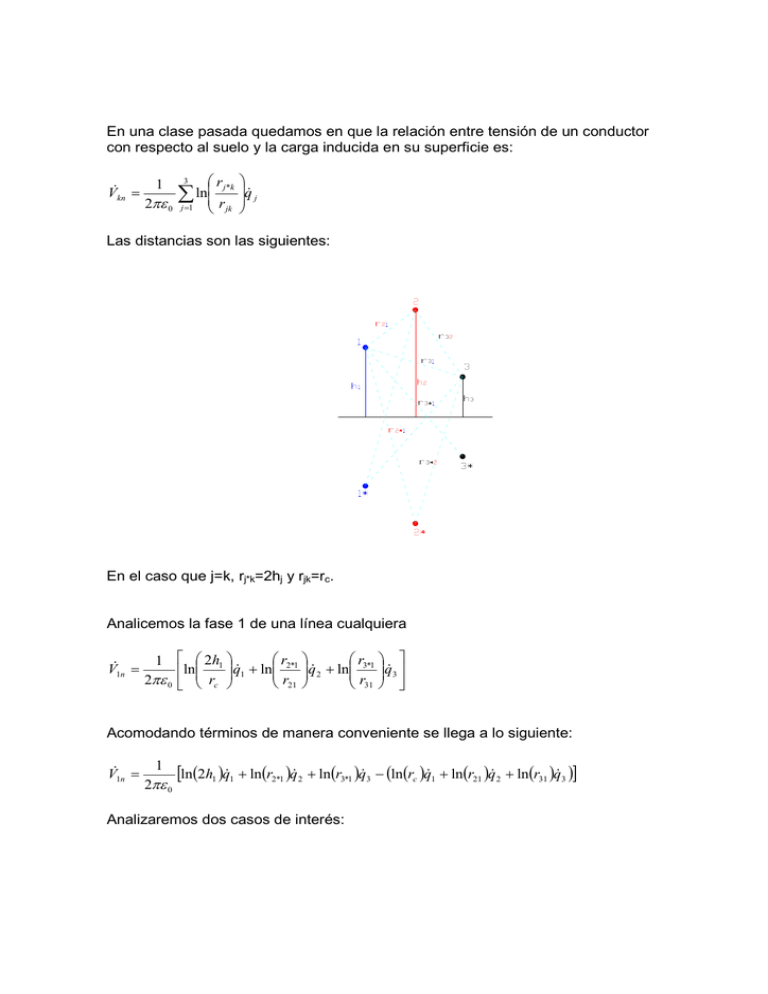
En una clase pasada quedamos en que la relación entre tensión de un conductor
con respecto al suelo y la carga inducida en su superficie es:
Vkn =
1
2πε 0
3
 r j *k 
q j

jk


∑ ln r
j =1
Las distancias son las siguientes:
En el caso que j=k, rj*k=2hj y rjk=rc.
Analicemos la fase 1 de una línea cualquiera
V1n =
r  
r 
1   2h1 
q1 + ln 2*1 q 2 + ln 3*1 q 3 
ln
2πε 0   rc 
 r21 
 r31  
Acomodando términos de manera conveniente se llega a lo siguiente:
V1n =
1
2πε 0
[ln(2h1 )q1 + ln(r2*1 )q 2 + ln(r3*1 )q 3 − (ln(rc )q1 + ln(r21 )q 2 + ln(r31 )q 3 )]
Analizaremos dos casos de interés:
1.-
Línea trifásica con disposición de fases en triángulo equilátero:
La expresión para la fase 1 será:
V1n =
1
2πε 0
[ln(2h1 )q1 + ln(r2*1 )q 2 + ln(r3*1 )q 3 − (ln(rc )q1 + ln(D )q 2 + ln(D )q 3 )]
En un sistema trifásico balanceado se debe cumplir que q1 + q 2 + q 3 = 0 .
Luego:
V1n =
V1n =
1
2πε 0
[ln(2h1 )q1 + ln(r2*1 )q 2 + ln(r3*1 )q 3 − (ln(rc ) − ln(D ))q1 ]
D 
1 
ln(2h1 )q1 + ln (r2*1 )q 2 + ln (r3*1 )q 3 + ln q1 
2πε 0 
 rc  
Si además suponemos que la línea está suficientemente alejada del suelo
se tendrá que r2*1 ≈ r3*1 ≈ 2h1
Ejemplo numérico:
Por reglamento eléctrico, lo mínimo que se debe tener un conductor de una
línea de 220 kV sobre el suelo son 7,32 [m]. Si consideramos una
separación entre fases de 5 [m], se tendrá que:
(14,64
(14,64
r2*1 =
r3*1 =
)
2
+ 2,5 2 = 14,85[m]
2
+ 5 2 = 15,47[m]
2h1 = 14,64[m]
)
Propuesto dejo rehacer el cálculo cuando la distancia al suelo es mayor (con 10 m
ya las cantidades se parecen más entre ellas). Lo importante es que las distancias
entre conductores sean menores que la altura de estos sobre el suelos.
Luego:
V1n =
D 
1 
(q1 + q 2 + q 3 ) ln (2h1 ) + ln q1 
2πε 0   rc  
0

D
1
V1n =
ln q1
2πε 0  rc 
Finalmente, la capacitancia es C1n =
2πε 0
D
ln 
 rc 
Lo mismo se tendrá para las demás fases.
Con esta expresión se puede tener el modelo de línea de transmisión con
un equivalente monofásico. La expresión anterior no significa que no
existan capacitancias entre fases (de hecho, las hay, y basta con escribir en
forma matricial la primera ecuación de este texto)
2.-
Línea trifásica con espaciamientos asimétricos
Volviendo a la expresión general de la fase 1:
1
ln ( 2h1 ) q1 + ln ( r2*1 ) q2 + ln ( r3*1 ) q3 − ( ln ( rc ) q1 + ln ( r21 ) q2 + ln ( r3*1 ) q3 ) 
V1n =
2πε 0 
En este caso no podemos factorizar nada de lo que está con signo menos
en paréntesis redondo. Si bien el resto de los términos que aproximamos
como iguales en la expresión anterior podríamos eliminarnos, los dejaremos
ahí por un momento.
Una transposición es una técnica constructiva que hace que cada fase
ocupe todas las posiciones en una línea, durante un tercio del recorrido.
Para llegar a una expresión útil para nuestro propósito, se hace el supuesto
que la carga es constante en cada conductor de fase (o al menos presenta
pequeñas variaciones), independiente de la posición que ocupa en la línea
durante un ciclo completo de transposición.
Considerando lo anterior, la tensión en cada fase será un promedio:
V Tramo1 + V1Tramo 2 + V1Tramo 3
V1nTranspuesto = 1
3
Es decir, la tensión de la fase 1 es el promedio de la tensión promedio del
conductor de la fase “azul”. Luego:
V1nTranspuesto =
( ln ( r2*1 ) + ln ( r3*2 ) + ln ( r3*1 ) ) q
1  ( ln ( 2h1 ) + ln ( 2h2 ) + ln ( 2h3 ) )
q1 +

2
2πε 0 
3
3
( ln ( r3*1 ) + ln ( r2*1 ) + ln ( r3*2 ) ) q − ln r q − ( ln ( r21 ) + ln ( r32 ) + ln ( r31 ) ) q
+
( c) 1
3
2
3
3
( ln ( r3*1 ) + ln ( r2*1 ) + ln ( r3*2 ) ) 
+

3

Factorizando y ordenando:
V1nTranspuesto =
(
)
1 
ln 2 3 h1h2 h3 q1 + ln
2πε 0 
(
3
r2*1r3*2 r3*1
) ( q
2
+ q3 ) − ln ( rc ) q1 − ln
(
3
r21r32 r31
) ( q
Y considerando que −q1 = q2 + q3 :
1   3 r21r32 r31
V1nTranspuesto =
ln 
rc
2πε 0  

 3 r2*1r3*2 r3*1
 − ln 

 23 h h h
1 2 3



  q1


Definiendo la distancia media geométrica como DMG = 3 r21r32 r31
 3 r2*1r3*2 r3*1
1   DMG 
V1nTranspuesto =
 ln 
 − ln  3
2πε 0   rc 
 2 h1h2 h3

La expresión anterior muestra cómo la
disminuye la capacitancia de una línea.

  q1


presencia de un plano de tierra
Si se considera nuevamente una línea con sus conductores alejados de la
tierra, se tendrá que r2*1 ≈ r3*1 ≈ r3*2 ≈ 2h1 ≈ 2h2 ≈ 2h3 . Luego
V1nTranspuesto =
 DMG 
2πε 0
ln 
 q1 ⇒ C1n =
2πε 0  rc 
 DMG 
ln 

 rc 
1
2
+ q3 ) 
