chuleta ch
Anuncio

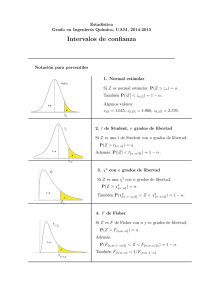
CONTRASTES SOBRE LA MEDIA: Rechazamos H0 a un nivel de significación α si: H0 H1 µ [ µ0 µ > µ0 µ µ µ0 µ < µ0 µ = µ0 µ γ µ0 σ2 conocida σ2 desconocida σ zα n σ x ≤ µ0 + z1−α n σ | x − µ0 | ≥ zα / 2 n s t n −1,α n s x ≤ µ0 + t n −1,1−α n s t n −1,α / 2 | x − µ0 | ≥ n x ≤ µ0 + x ≥ µ0 + CONTRASTES SOBRE LA VARIANZA: Rechazamos H0 a un nivel de significación α si: H0 H1 σ µ σ0 σ < σ0 µ conocida µ desconocida ∑ (x i − µ) 2 ≤ χ 2n ,1−α σ02 σ 02 2 χ s ≤ n − 1 n −1,1−α σ2 s 2 ≥ 0 χ2 n − 1 n −1, α n i =1 n σ [ σ0 ∑ (x σ > σ0 i =1 σ = σ0 σ γ σ0 n i − µ) 2 ≥ χ 2 σ 02 n ,α σ 02 ( x i − µ) 2 ≤ χ 2 ∑ − α n , 1 / 2 i =1 ó n 2 σ 02 ( x i − µ) ≥ χ 2 ∑ α n , / 2 i =1 2 2 σ 02 2 χ s ≤ n − 1 n −1,1− α / 2 ó 2 2 σ0 2 s ≥ n − 1 χ n −1, α / 2 CONTRASTES SOBRE DIFERENCIA DE MEDIAS: Rechazamos H0 a un nivel de significación α si: σ12 σ12 y σ22 desconocidas pero σ12=σ22 2 y σ2 conocidas H0 H1 µ1 - µ2 [ δ µ1 - µ2 > δ x − y ≥ δ + zα R p x − y ≥ δ + t n1 + n 2 − 2 , α S p µ1 - µ2 ≥ δ µ1 - µ2 < δ x − y ≤ δ − zα R p x − y ≤ δ − t n1 + n 2 − 2 , α S p µ1 - µ2 = δ µ1 - µ2 γ δ | x − y − δ | ≥ zα / 2 R p | x − y − δ |≥ t n1 + n 2 − 2 ,α / 2 Sp Rp = σ12 σ 22 + n1 n 2 Sp = (n1 − 1) S12 + (n 2 − 1) S22 n1 + n 2 − 2 1 1 + n1 n 2 S1 y S2 son las cuasivarianzas CONTRASTES SOBRE LA DIFERENCIA DE VARIANZAS: Rechazamos H0 a un nivel de significación α si: H0 µ1 y µ2 conocidas H1 n1 2 σ1 [ σ22 σ12 > σ2 2 ∑ (x i − µ1 ) 2 ∑ (y i − µ2 )2 ∑ (y i − µ2 )2 ∑ (x i − µ1 ) 2 i =1 n2 i =1 n2 σ1 2 ≥ σ2 2 σ12 < σ22 i =1 n1 i =1 σ1 2 = σ2 2 σ12 γ σ22 µ1 y µ2 desconocidas n ≥ 1 Fn1 ,n 2 ,α n2 s12 ≥ Fn1 −1,n 2 −1,α s 22 n2 Fn ,n ,α n1 2 1 s 22 ≥ Fn 2 −1,n1 −1,α s12 ≥ n1 2 ∑ ( x i − µ1 ) in=1 ≥ 2 2 ∑ ( yi − µ 2 ) i =1 ó n2 ∑ ( yi − µ 2 ) 2 i =1 ≥ n1 2 ∑ ( x i − µ1 ) i =1 n1 Fn ,n ,α / 2 n2 1 2 n2 Fn ,n ,α / 2 n1 2 1 s12 2 2 2 ≥ Fn1 −1,n 2 −1,α / 2 si s1 ≥ s 2 s2 ó 2 s2 2 2 s 2 ≥ Fn 2 −1,n1 −1,α / 2 si s1 < s 2 1