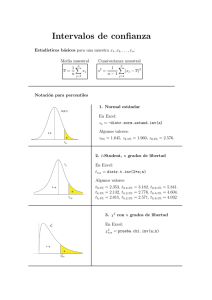
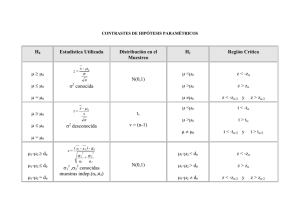
Contrastes de hipótesis paramétricos (Regiones de rechazo)
Anuncio

ESTADÍSTICA APLICADA Y MODELIZACIÓN. I.T. DISEÑO INDUSTRIAL. Contrastes de hipótesis paramétricos (Regiones de rechazo) Contrastes para la media µ de una distribución normal N (µ, σ) Varianza H 0 : µ = µ0 H 0 : µ = µ0 H 0 : µ = µ0 Ha : µ < µ0 Ha : µ 6= µ0 Ha : µ > µ0 σ x < µ0 − zα √ n σ |x − µ0 | > z α2 √ n σ x > µ0 + zα √ n S x < µ0 − zα √ n S |x − µ0 | > z α2 √ n S x > µ0 + zα √ n S x < µ0 − tα,n−1 √ n S |x − µ0 | > t α2 ,n−1 √ n S x > µ0 + tα,n−1 √ n Muestras conocida desconocida grandes n > 30 desconocida pequeñas n ≤ 30 Contrastes para la varianza σ 2 de una distribución normal N (µ, σ) H0 : σ 2 = σ02 H0 : σ 2 = σ02 H0 : σ 2 = σ02 Ha : σ 2 < σ02 Ha : σ 2 6= σ02 Ha : σ 2 > σ02 (n − 1)S 2 < χ21−α,n−1 σ02 i (n − 1)S 2 h 2 2 α α ∈ / χ ; χ 1− ,n−1 ,n−1 2 2 σ02 (n − 1)S 2 > χ2α,n−1 σ02 Inmaculada de las Peñas Cabrera. Dpto de Matemática Aplicada 1 ESTADÍSTICA APLICADA Y MODELIZACIÓN. I.T. DISEÑO INDUSTRIAL. Contraste bilateral para la diferencia de medias (µ1 − µ2 ) de dos distribuciones normales N (µ1 , σ1 ) y N (µ2 , σ2 ) H0 : µ1 = µ2 Ha : µ1 6= µ2 Varianzas Muestras Varianzas Región de rechazo s σ12 σ22 + n1 n2 s S12 S22 + n1 n2 |x1 − x2 | > z α2 Conocidas Grandes |x1 − x2 | > z α2 n1 +n2 > 30 n1 ' n2 s Desconocidas Iguales |x1 − x2 | > t α2 ,n1 +n2 −2 Sp 1 1 + n1 n2 Pequeñas n1 +n2 ≤ 30 s |x1 − x2 | > t α2 ,f Distintas S12 S22 + n1 n2 Contraste unilateral para la diferencia de medias (µ1 − µ2 ) de dos distribuciones normales N (µ1 , σ1 ) y N (µ2 , σ2 ) H0 : µ1 = µ2 Ha : µ1 < µ2 Varianzas Muestras Varianzas Región de rechazo s σ12 σ22 + n1 n2 s S12 S22 + n1 n2 x1 < x2 − zα Conocidas Grandes x1 < x2 − zα n1 +n2 > 30 n1 ' n2 s Desconocidas Iguales x1 < x2 − tα,n1 +n2 −2 Sp 1 1 + n1 n2 Pequeñas n1 +n2 ≤ 30 s Distintas x1 < x2 − tα,f Inmaculada de las Peñas Cabrera. Dpto de Matemática Aplicada S12 S22 + n1 n2 2 ESTADÍSTICA APLICADA Y MODELIZACIÓN. I.T. DISEÑO INDUSTRIAL. Contraste unilateral para la diferencia de medias (µ1 − µ2 ) de dos distribuciones normales N (µ1 , σ1 ) y N (µ2 , σ2 ) H0 : µ1 = µ2 Ha : µ1 > µ2 Varianzas Muestras Varianzas Región de rechazo s σ12 σ22 + n1 n2 s S12 S22 + n1 n2 x1 > x2 + zα Conocidas Grandes n1 +n2 > 30 x1 > x2 + zα n1 ' n2 s Desconocidas Iguales x1 > x2 + tα,n1 +n2 −2 Sp 1 1 + n1 n2 Pequeñas n1 +n2 ≤ 30 s Distintas donde Sp2 = x1 > x2 + tα,f (n1 − 1)S12 + (n2 − 1)S22 n1 + n2 − 2 f es el natural más próximo a S12 S22 + n1 n2 1 n1 + 1 S12 n1 !2 S12 S22 + n1 n2 y !2 1 + n2 + 1 S22 n2 !2 − 2 Contrastes para la razón de varianzas σ12 /σ22 de dos poblaciones normales N (µ1 , σ1 ) y N (µ2 , σ2 ) H0 : σ12 = σ22 H0 : σ12 = σ22 H0 : σ12 = σ22 Ha : σ12 < σ22 Ha : σ12 6= σ22 Ha : σ12 > σ22 S12 < F1−α;n1−1,n2−1 S22 S12 ∈ / [F1− α2 ;n1−1,n2−1 , F α2 ;n1−1,n2−1] S22 S12 > Fα;n1−1,n2−1] S22 Inmaculada de las Peñas Cabrera. Dpto de Matemática Aplicada 3 ESTADÍSTICA APLICADA Y MODELIZACIÓN. I.T. DISEÑO INDUSTRIAL. Contrastes para el parámetro p de una distribución binomial B(1, p) H0 : p = p 0 H0 : p = p 0 H0 : p = p 0 H a : p < p0 Ha : p 6= p0 H a : p > p0 s p̂ < p0 − zα s p0 (1 − p0 ) n |p̂ − p0 | > z α2 s p0 (1 − p0 ) n p̂ > p0 + zα p0 (1 − p0 ) n Contrastes para la diferencia de parámetros (p1 − p2 ) de dos distribuciones binomiales B(1, p1 ) y B(1, p2 ) H0 : p 1 = p 2 s 1 1 p (1 − p) + n1 n2 p̂1 < p̂2 − zα Ha : p 1 < p 2 H0 : p 1 = p 2 s |p̂1 − p̂2 | > z 1 1 + p (1 − p) n1 n2 α 2 Ha : p1 6= p2 H0 : p 1 = p 2 s p̂1 > p̂2 + zα 1 1 p (1 − p) + n1 n2 Ha : p 1 > p 2 siendo p= n1 p̂1 + n2 p̂2 n1 + n2 Contrastes para el parámetro λ de una distribución de Poisson P (λ) H0 : λ = λ0 H 0 : λ = λ0 H 0 : λ = λ0 Ha : λ < λ 0 Ha : λ 6= λ0 Ha : λ > λ 0 s s x < λ0 − zα λ0 n |x − λ0 | > z α2 λ0 n s x > λ0 + zα Inmaculada de las Peñas Cabrera. Dpto de Matemática Aplicada λ0 n 4