1 - Uprm

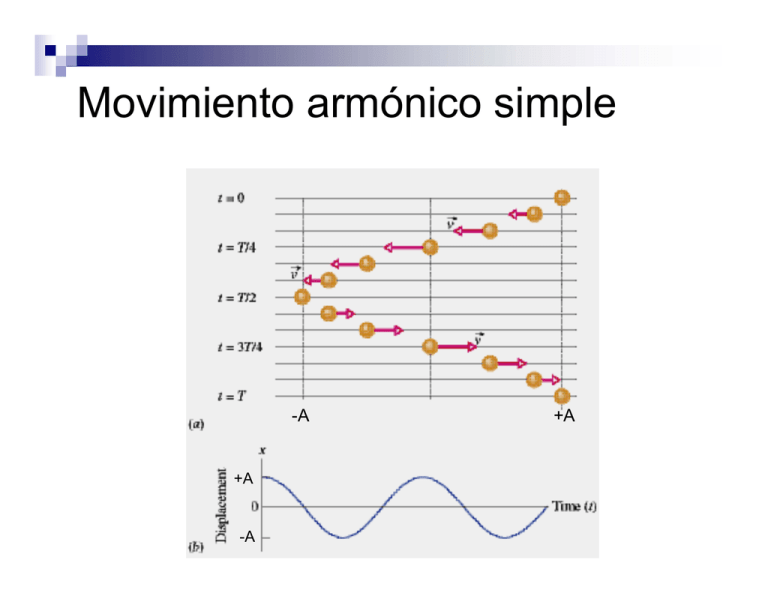
Movimiento armónico simple
-A
+A
-A
+A
Desplazamiento
fase
x(t ) = Acos(ω t + δ )
amplitud
desplazamiento
en tiempo t
tiempo
frecuencia angular
constante de fase o
ángulo de fase
Periodo, frecuencia angular y lineal
T
T
2π
ω (t + T ) + δ = ω t + δ + 2π ∴ ω =
= 2π f
T
Velocidad y aceleración en MAS
dx
v=
dt
v = −ωA sin (ω t + δ )
dv
a=
dt
2
a = −ω A cos(ω t + δ )
a = −ω x
2
Bloque atado a un resorte
F = −kx = ma
F = −kx
k
k
2
a = − x = −ω x ⇒ ω =
m
m
m
T = 2π
k
En MAS el periodo y la frecuencia no
dependen de la amplitud
Ejemplo:
Un objeto oscila con frecuencia angular ω=8 rad/s. Cuando
t=0, el objeto se encuentra en x0=4 cm con una velocidad
inicial v0=-25 cm/s. Calcula la amplitud y la constante de fase.
Escribe la posición x del objeto en función de t.
En general la posición y la velocidad están dados por
x(t ) = A cos(ω t + δ )
v = −ωA sin(ω t + δ )
2
⎛ v0 ⎞
A= x +⎜ ⎟ ,
⎝ω ⎠
2
0
v0
tan δ = −
ω x0
Ejemplo
Un bloque de 680 gramos es atado a un resorte de constante
elástica k=65 N/m. El bloque es movido a una distancia de 11
cm a la derecha del punto de equilibrio y soltado de reposo.
Calcula (a) la frecuencia angular, la frecuencia lineal y el
periodo del movimiento, (b) la amplitud de la oscilación, (c) la
magnitud de la velocidad máxima (en que lugar ocurre?), (d)
la magnitud de la aceleración máxima, (e) la constante de
fase y (f) el desplazamiento para cualquier tiempo t.
Relación entre movimiento circular y MAS
ω
Supongamos que la
partícula completa una
vuelta en tiempo T. La
velocidad angular es:
∆θ 2π
=
ω=
T
∆t
En el tiempo T, la sombra
de la partícula completa
una oscilación.
Si la sombra completa una
oscilación en T segundos,
cuántas oscilaciones
completa en 1 segundo?
Haz una proporción.
1 osc en T seg
f osc en 1 seg
f osc 1 osc
=
1 seg T seg
1 ω
f = =
T 2π
t;0
δ
x
t=0
2π
ω = 2π f =
T
x = A cos θ
∆θ θ − δ
=
ω=
∆t
t −0
θ = ωt + δ
∴ x = A cos (ω t + δ )
Energía en MAS
1 2 1 2
2
U = kx = kA cos (ω t + δ )
2
2
1 2 1
2 2
2
K = mv = mω A sin (ω t + δ )
2
2
1 2 2
K = kA sin (ω t + δ )
2
E total
1 2
= kA
2
En MAS la energía es
proporcional al cuadrado de
la amplitud.
1 2
Etotal = K + U = kA
2
1 2 1 2 1 2
mv + kx = kA
2
2
2
k 2
2
v=±
A −x )
(
m
v = ±ω A − x
2
2
Ejemplo
Un bloque de 0.5 kg es conectado a un resorte de constante
elástica k=20 N/m y puesto a oscilar en una mesa horizontal
sin fricción con una amplitud de 3 cm. Calcula (a) la energía
total del sistema, (b) la velocidad del bloque cuando x=2 cm y
(c) la energía cinética y la potencial cuando x=2 cm.
Péndulo Simple
2
d s
Ft = − mg sin φ = m 2
dt
s = Lφ
d φ
g
= − sin φ
2
L
dt
2
Si el ángulo es menor de 1 radian,
entonces
sin φ ≈ φ
Péndulo Simple
Con esta aproximación, la
ecuación de movimiento es
d φ
g
=− φ
2
dt
L
g
2
α = − φ = −ω φ
L
g
L
∴ω =
, T = 2π
L
g
2