Econometría final junio 8
Anuncio

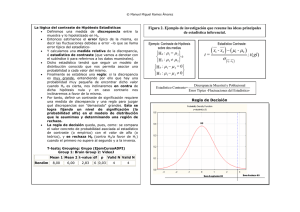
EXAMEN ECONOMETRIA L.A.D.E. 1º y 2º SEMESTRE 1 DESCRIPCIÓN DEL EXAMEN La duración del examen es de 2 horas y media. TEORÍA: 2 preguntas a desarrollar. PRÁCTICA: 1 problema. TEORÍA PARTE I: TEORÍA. 1) Incumplimiento de hipótesis básica del modelo de regresión lineal. Desarrolla, de forma detallada, causas, problemas que genera y contrastes para el Cambio de estructura. 2) Exprese la forma desarrollada del modelo de series temporales, estimado con datos trimestrales: ARIMA (1,2,1) SARIMA 4 (1,1,0) PARTE II: PRÁCTICA. Se ha estimado el siguiente modelo para explicar la evolución el número de MUERTOS en accidente de automóvil, en función de las variables: - Conductor NOVEL - Conductores DENUNCIADOS - Antigüedad del automóvil PARQUE Con la información proporcionada, analizar la bondad del modelo y contraste el cumplimiento de las diferentes hipótesis básicas. d s = 1´54 di = 0´98 C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid Tel.: 91 371 92 83 EXAMEN ECONOMETRIA L.A.D.E. C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid 1º y 2º SEMESTRE 2 Tel.: 91 371 92 83 EXAMEN ECONOMETRIA L.A.D.E. 1º y 2º SEMESTRE 3 Solución:________________________________________________________________________ MUERTOSt = β0 + β1 ⋅ NOVELESt + β2 ⋅ PARQUEt + ut ; ∀ t = 1, 2,⋯,16 - Los coeficientes βi son individualmente significativos pues t − Statistic > 2 . - Los coeficientes (pendientes) conjuntamente son significativos pues F − statistic > 4 . - El modelo posee un R 2 = 0´859498 el cual nos indica que la regresión explica el 85´94% de la variación de la variable endógena. C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid Tel.: 91 371 92 83 EXAMEN ECONOMETRIA L.A.D.E. - 1º y 2º SEMESTRE 4 Contraste F-statistic de variable omitida: Omitted Variable: DENUNCIAS H 0 :La variable DENUNCIAS no es relevante o significativa. H1 :La variable DENUNCIAS es relevante o significativa. Como el estadístico F − statistic > / 4 no rechazamos Ho luego la variable está bien omitida no incurrimos en Error de Especificación. - Contraste F-statistic de variable irrelevante: Redundant Variable: PARQUE H 0 :La variable PARQUE es irrelevante o no significativa. H1 :La variable PARQUE no es irrelevante o es significativa. Como el estadístico F − statistic > 4 rechazamos Ho luego la variable está bien incluida no incurrimos en Error de Especificación, esto ya se sabia con el contraste individual de significación del parámetro β2 . - Contraste Ramsey RESENT Test: H 0 :El modelo es lineal. H1 :El modelo no es lineal. Como el estadístico F − statistic > 4 rechazamos Ho luego el modelo no es lineal por ello incurrimos en un Error de Especificación. Detectada la no linealidad, la solución conllevaría determinar cuáles son las potencias y productos cruzados concretos de las variables explicativas que mejor recogen sea no linealidad. - Contraste Chow Breskpoint Test: 1997 H 0 :No existe cambio estructural β1Submuestra = β2 Submuestra H1 : Si existe cambio estructural β1Submuestra ≠ β2 Submuestra Como el estadístico F − statistic > / 4 no rechazamos Ho luego el modelo no posee cambio de estructura. - White Heteroskedasticity Test: H 0 :No existe Heterocedasticiadad (Var = cte) H1 : Si existe Heterocedasticiadad (Var = / cte) Como el estadístico Obs * R − squared posee una probabilidad superior a 0´05 (0´121098 > 0´05) no rechazamos Ho luego el modelo no presenta Heterocedasticidad. C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid Tel.: 91 371 92 83 EXAMEN ECONOMETRIA L.A.D.E. A) 1º y 2º SEMESTRE 5 Contrastes para estudiar la existencia o no de autocorrelación en l modelo: Contraste de Durbin Watson H 0 :No existe autocorrealción de primer ordencambio estructural (ρ = 0) H1 : Si existe autocorrealción de primer ordencambio estructural (ρ ≠ 0) 4 Autocorrelación negativa de primer orden 4-di Zona de duda 4-ds 2 Ausencia de autocorrelación de primer orden ds = 1´54 Zona de duda di= 0´98 Autocorrelación positiva de primer orden 0 Como el estadístico dw se sitúa entre di y ds Zona de duda no sabemos si posee o no autocorrelación el modelo, esto es una de las dificultades que presenta el contraste DW. Se han propuesto diversos perfeccionamientos para reducirlas o eliminarlas. Para poder afirmar o no la existencia de autocorrelación nos proporciona el correlograma de los errores y el test de Breusch-Godfrey. B) Correlograma fijándonos en el como ninguna de la barras sobrepasan las bandas de confianza podemos decir que el modelo no presenta autocorrelación de primer orden pero como es un test grafico y son poco potentes no ayudamos del siguiente tes. C) Bresuch-Godfrey Serial Correlation LM Test: H 0 :No existe autocorrelacion de primer orden (ρ = 0) H1 : Si existe autocorrelacion de primer orden (ρ ≠ 0) C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid Tel.: 91 371 92 83 EXAMEN ECONOMETRIA L.A.D.E. 1º y 2º SEMESTRE 6 Como el estadístico Obs * R − squared posee una probabilidad superior a 0´05 (0´548956 > 0´05) no rechazamos Ho luego el modelo no presenta autocorrelación de primer orden conclusión a la que llegábamos con el correlograma. - Nos fijamos en el Histograma: 1. Mean 5´12e-13 ≈ 0 luego la media del error es cero. 2. Skewness -0´615776 < 0 El coeficiente de asimetría nos indica que la distribución es asimétrica a la izquierda. 3. Kurtosis 2´597875 ≈ 3 lo cual nos indica que los errores siguen una Normal, pero como este coeficiente no es del todo seguro no ayudamos del estadístico Jarque.Bera. 4. Estadístico Jarque-Bera H 0 :Los errores siguen una distribucion Normal (ut ∼ Normal ) H1 :Los errores NO siguen una distribucion Normal (ut ∼ / Normal ) • Estadístico JB= 1´118949 • Valor Crítico: 6 • Decisión: como el Estadístico es menor que 6 no rechazamos Ho, por ello los errores siguen una Normal, conclusión a la que llegábamos con el coeficiente de Curtosis. C/ Villardondiego, 17 y 19 (Posterior). VICALVARO 28032 Madrid Tel.: 91 371 92 83