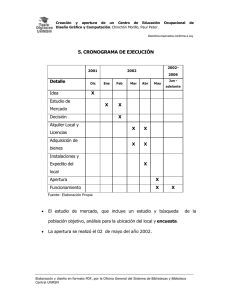
capitulo ii marco teorico
Anuncio

Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley CAPITULO II MARCO TEORICO 2.1.- ENFERMEDADES Y VIAS DE TRANSMISIÓN SEXUAL El SIDA (Síndrome de Immuno Deficiencia Adquirida) es causado por el virus VIH (Virus de Inmunodeficiencia Humana). El SIDA es la etapa final de un largo proceso de destrucción del organismo humano por el lentivirus, mal llamado VIH. Este virus destruye el sistema inmunológico del cuerpo humano porque tan pronto entra al cuerpo humano ataca al sistema nervioso central, el cerebro y la médula espinal. Aún antes de inutilizar a las células T4, que controlan el sistema de inmunidad y defensa que el cuerpo posee para luchar contra las infecciones, convierte a las T4 en aliadas para diseminar la enfermedad a través de todo el organismo. El virus del SIDA destruye las células del cerebro causando un deterioro mental progresivo. Todos los órganos importantes son blancos de este virus mortal, el corazón, los pulmones, los riñones, el hígado, el páncreas, los músculos, la piel, etc. La gran tragedia es que no hay forma de sacar al virus del SIDA una vez que el individuo es infectado, ya que al formar parte de su DNA la persona queda genéticamente estampada para siempre como un portador del virus. No hay droga que pueda separar al virus de los genes de las células que ha penetrado. Para ello sería necesario matar todas las células infectada matando al individuo. Otra terrible característica del virus de SIDA es que una vez dentro del cuerpo nunca está en estado durmiente o inactivo, sino que se mantiene desde el principio mutando y replicándose constantemente a través de todas las fases de la enfermedad. No se trata simplemente de un proceso infeccioso, sino de una enfermedad infecciosa degenerativa con una tasa de mortalidad del 100%. El VIH se transmite por tres vías: a) Vías de Transmisión Sexual: Por el intercambio de fluidos como el semen o el flujo vaginal. Estas vías se produce durante las relaciones sexuales sin protección, sin el uso de condones, el VIH puede entrar al cuerpo por relaciones sexuales a través del ano, la vagina, el pene o la boca. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley En el sexo anal hay riesgo tanto para el que penetra (activo) como para el que es penetrado (pasivo). El virus no puede cruzar la barrera del látex del condón, si este se usa de vez en cuando, la seguridad no es 100%. El VIH se puede transmitir sin que no haya eyaculación, por lo que es necesario usar el condón desde el inicio de la penetración. La mayoría de los hombres gay infectados con VIH lo adquirieron por el sexo penetrativo sin protección. El sexo oral es menos riesgoso que el sexo anal. Existen formas de reducir el riesgo de VIH por esta vía, lo más seguro es usar condón para esta práctica. b) Vías de Transmisión Sanguínea: Se origina mediante las transfusiones de sangre, que pasa directamente al torrente sanguíneo. Al compartir agujas o jeringas para medicamentos o drogas, es decir al entrar la aguja a la piel pasando directamente a la vena de la persona. Las transfusiones de sangre son examinadas desde 1987, la sangre que se encuentra contaminada es desechada. c) Vías de Transmisión Vertical: La madre infecta al niño durante el embarazo, durante el parto o al amamantarlo. Durante la lactancia, el bebé puede adquirir el virus. A diferencia de otros virus como el de la gripe, resfriado, el VIH no se transmite por el aire, al tocarse, o por el contacto diario. En algunas ocasiones, no sabemos si la persona con la que mantenemos o vamos a tener relaciones sexuales vive con el VIH, incluso puede que no lo sepa ni él ni ella. Por ello, durante la penetración vaginal o anal es importante el uso correcto del preservativo ya que éste evitará el contacto, a través de pequeñas heridas que se producen durante las relaciones sexuales, con el semen o flujo vaginal infectados. Además, con el condón podemos evitar otras enfermedades de transmisión sexual. 2.1.1.- ENFERMEDADES DE TRANSMISIÓN SEXUAL Las enfermedades de transmisión sexual (ETS), son infecciones que pueden ser transmitidas de una persona a otra ya sea por el contacto sexual oral, anal o vaginal; algunas de estas enfermedades son curables si se tratan a tiempo. Este tipo de infecciones se dan en un importante número de hombres con vida sexual activa. Entre la extensa lista se encuentran aquellas que pueden ser tratadas Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley • Como sífilis, gonorrea, clamidia y otras infecciones en la zona púbica • Y otras ante las que no se conoce cura alguna (VIH, Hepatitis A, B o C, HPV, etc.). No caben dudas en que la mejor forma de prevención ante estos virus consiste en la protección en contactos sexuales que vayan desde la simple frotación de miembros, el sexo oral hasta la penetración. Las ETS se pueden prevenir: a) Al abstenerse de todo tipo de contactos sexual: Oral, anal o vaginal b) Usando condón cada vez que tenga relaciones sexuales. Los síntomas de las ETS son: a) Secreciones anormales del pene, ano o vagina. b) Dolor o ardor al orinar o al defecar . c) Llagas, protuberancias o ampollas en los genitales. d) Comezón en el área genital. Los tratamientos, varían dependiendo de la ETS, si se detecta alguna de las enfermedades de transmisión sexual, es importante visitar el médico, para el tratamiento adecuado. Las ETS son infecciones que pueden tener serias consecuencias para ambos sexos. Si no se les trata a tiempo pueden causar: daños en los órganos sexuales, en el sistema nervioso o producir ceguera. 2.1.2.- TIPOS DE SEXUALIDAD • BISEXUAL: Persona (hombre o mujer) que tiene potencialmente una atracción sexual por individuos de ambos sexos. • HOMOSEXUAL: Persona (hombre o mujer) que tiene potencialmente una atracción sexual por individuos del mismo sexo. • HETEROSEXUAL: Persona (hombre o mujer) que tiene potencialmente una atracción sexual por individuos del sexo opuesto. • GAY: Hombre homosexual. Traducido al español: "Alegre", originalmente usaban este término los homosexuales que se mostraban a la sociedad como tales, sintiéndose orgullosos y alegres por su orientación sexual. • LESBIANA: Mujer homosexual. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley a) BISEXUALIDAD Bisexualidad es el potencial de estar erótica o románticamente atraído por personas de cualquier sexo. Así mismo, un bisexual es aquella persona que siente una atracción erótica por individuos de ambos sexos. Sin embargo, definir la identidad sexual de cada individuo no es tarea fácil. Definirla es algo muy personal, muchos individuos que mantienen relaciones sexuales con miembros de ambos sexos pueden no considerarse o llamarse bisexuales; quizás se consideren más como heterosexuales, o más como gays o lesbianas. Para entender esto podemos ejemplificarlo de la siguiente manera: el hecho de que un hombre tenga contacto sexual con una mujer, no significa necesariamente que ella en particular le atraiga sexualmente; puede ser que él únicamente quiera guardar apariencias o demostrarse a sí mismo algo. Ahora bien, en el caso de la bisexualidad, se aplica lo mismo: una persona que se sienta ya sea homosexual o heterosexual y tenga relaciones con ambos sexos no es necesariamente bisexual. Esta persona tendrá la identidad que internamente mejor le venga, con la que se sienta más a gusto. Sucede algo similar en el caso contrario. Puede ser que una persona se considere así misma bisexual debido a sus sentimientos por ambos géneros, pero que mantenga relaciones con persona(s) de un mismo género. Aquí se aplica nuevamente lo de la identidad: esta persona se siente bisexual, y aunque tiene una predilección o interés por involucrarse con un solo sexo, su sentir es para con ambos sexos a fin de cuentas. Aquí podría entrar el caso de un bisexual monógamo, lo cual es perfectamente válido, siempre y cuando así lo quiera y decida la persona. Ahora bien, un bisexual no se siente forzosamente atraído por hombres y por mujeres de igual manera. Una persona bisexual (hombre o mujer) puede preferir las relaciones con mujeres por encima de las relaciones con hombres, o preferir las relaciones con hombres por sobre las relaciones con mujeres, o bien, tener la misma preferencia por ambos sexos, concibiendo el amor erótico en este último caso, como un estado donde no importa el sexo de la pareja, sino su carácter. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley b) HOMOSEXUALIDAD Una persona homosexual es aquella persona que siente una atracción erótica por individuos del mismo sexo. Nuevamente aquí sucede lo mismo a la hora de que una persona se define como persona homosexual. El hecho de que una persona mantenga contacto sexual o erótico con personas de su mismo sexo, no significa forzosamente que sea homosexual. Muchos hombres y mujeres auténticamente heterosexuales llegan a tener este tipo de relaciones con individuos de su mismo sexo por el simple hecho de probar o demostrar algo, pero esto únicamente pudiera representar para ellos una simple experiencia, sin que ello repercuta en su orientación sexual básica. c) HETEROSEXUALIDAD Expertos de la universidad californiana de Berkley, Estados Unidos, concluyen que partiendo de la longitud de los dedos del feto, se puede determinar su orientación sexual. Según un estudio publicado en la revista Nature, la inclinación sexual de los seres humanos puede tener su origen en la exposición a los andrógenos u hormonas masculinas en el útero materno. Los autores del estudio, el doctor Marc Breelove y sus colaboradores, señalan que las mujeres heterosexuales pueden haber estado sometidas a menor hormonas masculinas en el útero, resultados similares en el caso de los hombres. Según Los Dedos: Los investigadores basan sus resultados en un patrón poco común: la longitud de los dedos del feto. En su opinión, las mujeres tienen menor diferencia entre sus dedos índice y anular que los hombres, quienes suelen tener el índice más corto que el anular debido a la mayor exposición a andrógenos en el útero. Por otra parte, los científicos han establecido otro patrón más a la hora de prever la orientación sexual del bebé. Según el equipo investigador, cuantos menos hermanos tenga un hombre, mayor tendencia a la heterosexualidad mostrará. La causa, en su opinión, es que el útero ha estado expuesto menores veces a las hormonas masculinas en los embarazos previos. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 2.2.- CONCEPTOS BÁSICOS DE ANÁLISIS FACTORIAL DE CORRESPONDENCIAS 2.2.1.- ANÁLISIS FACTORIAL DE CORRESPONDENCIAS SIMPLES 2.2.1.1.- INTRODUCCION El Análisis Factorial de Correspondencia (AC), es una técnica exploratoria del Análisis Multivariante especialmente para analizar tablas de contingencia. Técnica originaria de la escuela estadística francesa. El Análisis Factorial de Correspondencia permite estudiar las relaciones de interdependencia entre variables categóricas (no métricas), por tanto guarda cierta analogía con la prueba Chicuadrado y el coeficiente de concordancia de Kendall. Es una técnica de composición, que se ha ido haciendo mas popular para la reducción dimensional y la elaboración de mapas perceptuales; debido a que el mapa perceptual se basa en la asociación entre objetos y un conjunto de características descriptivas o atributos especificados por el investigador. Esta técnica tiene la ventaja que para su uso no se hace ninguna conjetura respecto a la distribución de probabilidad de la población de la cual se extrajo la muestra multivariante. Esta técnica va más allá de analizar la relación existente entre las variables, porque permite determinar cómo está estructurada esta asociación, describiendo “proximidades” que permiten identificar “categorías causa de asociación” . Entre las técnicas de composición, el Análisis Factorial es el mas parecido; pero el Análisis de Correspondencia va mas allá del Análisis Factorial. Su aplicación mas directa es la representación de la “correspondencia” de categorías de variables, particularmente aquellas medidas con escalas nominales. Esta Correspondencia es la base de desarrollo de mapas perceptuales. Los beneficios del Análisis se basa en sus capacidades únicas para presentar filas y columnas, por ejemplo etiquetas y atributos en un mismo espacio. Los resultados se presentan gráficamente sobre ejes de coordenadas, el cual ayuda en la interpretación de los resultados. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 2.2.1.2.- ANTECEDENTES HISTORICOS Su origen y autoría es difícil de determinar, por que es una conjunción de métodos estadístico matemáticos descubiertos y redescubiertos bajo ópticas distintas por diferentes autores. Entre ellos, podemos citar a Richardson y Kuder en 1933, Horst en 1935, Hirschfeld en 1935, Fisher en 1940, Guttman en 1941 o Hayashi en 1952. Así, J. P. Benzécri en su libro Historia y Prehistoria del Análisis de Datos dice en relación a los trabajos de Guttman, Fisher y Hayashi: “La priorité de ces auteurs est certaine: la seule originalité que puissent revendiquer les chercheurs français est d’avoir conjugué, avec une méthode découverte indépendamment plusieurs auteurs, des idées et des problèmes multiples dont la synthèse n’était pas faite.” Es en 1962 cuando aparece por primera vez el nombre de Análisis de Correspondencias en los primeros trabajos de Benzécri, quien en 1965 dirige la tesis de B. Escofier en la Facultad de Ciencias de Rennes (se muestran todas las propiedades algebraicas y geométricas). El término “correspondencia” fue usado para denotar el sistema de asociaciones entre los elementos de dos conjuntos, las filas y las columnas de una tabla de contingencia. Actualmente, debido a la facilidad operacional aportada por las computadoras, se aplica a diversas tablas de grandes dimensiones. El AC es muy empleado en todas las ciencias, en especial en las Ciencias Sociales. En investigación de mercados (posicionamiento de productos, imagen de marca, eficacia publicitaria, etc.) 2.2.1.3.-ANALISIS DE CORRESPONDENCIAS Y OTROS METODOS Tradicionalmente, la asociación entre variables categóricas se realizaba con métodos bivariantes. El Análisis de Correspondencia nos aportará información que de ningún modo nos da la Chi-cuadrado (X2 ) u otra medida de asociación en términos de existencia o no de relación entre las variables, de la intensidad de la misma. El AC calculará perfiles, inercias, contribuciones, etc., de las filas y/o columnas de la tabla de contingencia y permite analizar la posible relación entre las variables de modo gráfico en un espacio multidimensional tal que, previo cálculo por filas y columnas de las puntuaciones de Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley la tabla, las diversas categorías de las variables estarán representadas gráficamente más próximas o alejadas en las diversas dimensiones en función de su grado de similitud o diferencias. Los métodos multivariantes más conocidos para variables métricas son: Análisis de Componentes Principales (ACP), Análisis Factorial (AF) y Análisis Canónico. Mientras que cuando se trata de variables categóricas no métricas el Análisis de Correspondencia es el idóneo y mas eficaz. En una tabla de contingencia, la semejanza entre dos filas, por una parte, y entre dos columnas, por otra, se expresa de manera totalmente simétrica. Dos filas se consideran próximas, si se asocian del mismo modo al conjunto de las columnas, es decir, si ellas se asocian demasiado (o demasiado poco) a las mismas columnas; considerando "demasiado" y "poco" con respecto a la situación de independencia. Simétricamente, dos columnas están próximas si se asocian del mismo modo al conjunto de las filas. 2.2.1.4.- OBJETIVOS En el Análisis de Correspondencias Simples (ACS) se analizan dos variables categóricas. • Reducir la dimensión en el estudio de las relaciones de interdependencia entre variables categóricas, presentadas en forma de tablas de contingencia. • Convertir las categorías de la tabla de frecuencias (filas y columnas) en un menor número de dimensiones. • Analizar cómo está estructurada esta asociación (relación), describiendo “proximidades” que permitan identificar “categorías causas de asociación”. • Procesar datos de encuestas (variables o items categóricos) (Aplicación). 2.2.1.5.-TABLAS DE CONTINGENCIA Y DE FRECUENCIAS E INDEPENDENCIA DESCRIPTIVA EL Análisis Factorial de Correspondencia de una tabla de contingencia persigue cuatro objetivos fundamentales los que son importantes detallar para justificar este método: • Analizar toda la información contenida en una tabla de contingencia. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley • Representar gráficamente la estructura de una tabla de contingencia. • Producir estadísticas de control complementarias. • Analizar la estructura de una tabla de contingencia respetando el hecho que la misma resume una relación simétrica entre los caracteres observados. Una tabla de contingencia es una tabla estadística que resume la observación simultánea de dos características dadas de dos conjuntos de unidades de observación (población observada). Si el objetivo de lo observado es describir la manera en que esas características se asocian entre ellas a través de las co-ocurrencias observadas, esa tabla estadísticas constituye un resumen adecuado de la observación. Consideremos una población o muestra con n.. unidades (respuestas) sobre los que se pretende analizar simultáneamente dos variables categóricas, digamos X que tiene I categorías y la variable Y que tiene J categorías; la tabla de frecuencias bidimensional que describe a estas n.. unidades (respuestas) se llama tabla de contingencia (doble entrada): TABLA DE CONTINGENCIA TABLA T(I , J) Categorías 1 1 n11 : : variable i ni1 x : : I nI1 total n.1 ..... ..... ..... ..... ..... variable y j ..... J n1j ..... n1J : : nij ..... niJ : : nIj ..... nIJ n.j ..... n.J total n1. : ni. : nI. n.. NOTACIONES: • nij : Frecuencia Bidimensional Corresponde a la cantidad de individuos observados que presentarán simultáneamente la modalidad i de la variable X y la modalidad j de la variable Y. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley • ni. : Es el i- esimo elemento del margen derecho de la tabla T (no depende de J), corresponde a la cantidad de individuos observados que presenta la modalidad i de la variable X, este elemento esta definido por la expresión: ni . = • J ∑n ij j =1 n.j : Es el j-esimo elemento del margen inferior de la tabla T (no depende de I), corresponde a la cantidad de individuos observados que presentan la modalidad j de la variable Y, este elemento queda definido por la expresión: I = ∑ nij .j n • i =1 n.. : Es la suma de todas las celdillas de la tabla T, corresponde al total de individuos observados. Este elemento es definido así: I J I J i =1 j =1 n.. = ∑∑ nij = ∑ ni. = ∑ n. j i =1 j =1 Frecuentemente se considera la tabla de frecuencias relativas, esta tabla indica el porcentaje de elementos que simultáneamente tiene dos categorías, así: TABLA DE FRECUENCIAS RELATIVAS TABLA F(I , J) Categorías variable X 1 : i : I total 1 f11 : fi1 : fI1 f.1 ..... ..... ..... ..... ..... variable Y j ..... f1j ..... : fij ..... : fIj ..... f.j ..... J f1J : fiJ : fIJ f.J total f1. : fi. : fI. f.. NOTACIONES: Definimos los elementos de una tabla (I , J): • Frecuencia Relativa Conjunta: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley f ij = n n ij .. En una tabla de frecuencias, cada celdilla es una proporción. El valor de cada celdilla corresponde a la proporción de individuos observados en la población que presentan simultáneamente el carácter Xi de la variable X y el carácter Yj de la variable Y. • Frecuencias Marginales: = i. f f .j = n n n n .j .. • i. n ∑ n J = j =1 .. I =∑ i =1 n n ij ∑ f j =1 .. = ij J = I ∑f i =1 .. ij ∀ i ∈ i = ⟨1, 2 , ...... I ⟩ ij ∀j ∈ j = ⟨1, 2,......... J ⟩ La suma total o la suma de los márgenes es evidentemente igual a 1, puesto que la tabla de frecuencias relativas se obtiene dividiendo la tabla de contingencia por n.. f .. = I J ∑∑ i =1 j =1 n n ij .. = 1 n I J ∑∑n .. i =1 j =1 ij = n n .. =1 .. En el caso particular de la observación, sobre n unidades, de dos características (variables cualitativas) compuestas de tres niveles o modalidades (atributos) cada una, se resume lo observado mediante una tabla de tres líneas y tres columnas, cuya notación general presentamos a continuación: TABLA T(3 , 3) Características Variable X X1 X2 X3 n.j Y1 n11 n21 n31 n.1 Variable Y Y2 Y3 n12 n13 n22 n23 n32 n33 n.2 n.3 ni. n1. n2. n3 . n.. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley En ese caso decimos que la tabla T es de dimensión (3 , 3). Dividiendo las celdillas de la tabla T(3 , 3) entre n.. , obtenemos la tabla F(3 , 3), cuyos elementos se designan de la siguiente manera: TABLA F(3 , 3) Características Y1 f11 f21 f31 f.1 X1 X2 X3 f.j Variable X Variable Y Y2 Y3 f12 f13 f22 n23 f32 n33 f.2 f.3 fi. f1. f2. f3 . f.. Las variables son independientes si se cumplen una de las siguientes condiciones: 1) 2) f f ij = i/ j f f = f i. .j ∀ i, j f i. j/i = f .j ∀i, j 2.2.1.6.- DEFINICIÓN DE LOS PERFILES DE LOS ELEMENTOS DE LA TABLA F Los perfiles en línea y en columna de dicha tabla se obtienen dividiendo los valores de cada celdilla por el valor marginal correspondiente. Se puede analizar perfiles filas o perfiles columnas, ambos planteamientos producen los mismos resultados, filas y columnas juegan un papel simétrico en el análisis. Se denomina perfil de la fila i a la distribución de frecuencias de las categorías de la variable Y condicionada a las categoría de la variable X: H H i i f = f = H i1 i. i1 f f ,H , i2 i. i2 f f ,....., H ,....., i. iJ iJ i = 1,2,....., I i = 1,2,....., I Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley TABLA DE PERFILES FILA Categorías 1 H11 : Hi1 : HI1 1 : i : I Variable X variable Y j ..... H1j ..... : Hij ..... : HIj ..... ..... ..... ..... ..... J total H1J 1 : : HiJ 1 : : HIJ 1 Se denomina perfil de la columna j a la distribución de frecuencias de las categorías de la variable X condicionadas a las categorías de la variable Y: F F j j = = f f F 1 j , . j 1 j , f f F 2 j , ...., . j 2 j , ...., f f F Ij j = 1 , 2 , ...., J . j Ij j = 1, 2 , ...., J TABLA DE PERFILES COLUMNA Categorías variable X 1 1 F11 : : i Fi1 : : I FI1 total 1 variable Y ..... j ..... ..... F1j ..... : ..... Fij ..... : ..... FIj ..... ..... 1 ..... J F1J : FiJ : FIJ 1 2.2.1.7.- ESPACIO DE REPRESENTACION La representación analógica que hemos dado de una tabla de contingencia nos conduce a una apreciación visual de la posición relativa de puntos en un espacio deformado por los efectos de perspectivas. Esto puede producir proximidades o alejamientos ficticios entre los puntos, Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley es decir relaciones inexistentes. Podemos evitar esos errores de lectura completando esos gráficos con una relación digital de la posición relativas de esos puntos en esos espacio. Podemos también evaluar la posición relativa de una serie de puntos de esos espacios, calculando la suma de esas distancias, dos a dos, de esos puntos. Recordando el teorema de Pitágoras, podemos calcular fácilmente las distancias entre dos puntos de un plano. Consideremos la figura I: FIGURA I Y A” A D(A , B) B” C B A’ B’ X La distancia entre A y B esta dada entonces por la expresión : d ( A ,B ) = ( B '− A ') + ( B "− A") 2 2 Como veremos mas adelante esta relación se generaliza al caso de puntos representados en espacios de tres o mas dimensiones. La distancia entre dos puntos A y B, en un espacio de tres dimensiones, esta dada por la relación siguiente: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley d 2 ( B '− A ') + ( B ''− A '') + ( B "'− A "') = ( A ,B ) 2 2 La expresión general de esta distancia entre dos elementos líneas de una tabla T(I , J) es la siguiente: d (i ,i ') = ∑ (nij − ni ' j ) J 2 ∀i , i ' j =1 La distancia entre dos elementos columna de una tabla T(I, J) es la siguiente: d ( j , j ') = ∑ (n ij− n ij ') I 2 ∀j , j ' i =1 Cuando comparamos dos elementos línea (o columna) de una tabla establecemos una relación de similitud de diferencias entre ellos. En términos de distancias en un espacio euclidiano, esas similitudes y diferencias se expresan por el hecho que los puntos-elementos del espacio se superponen (distancia nula) o no (muestran una distancia entre ellos). La distancia entre dos puntos de un espacio euclidiano no puede ser mas que nula o de valor positivo. Es decir que para todo par de elementos de la tabla: d ( i , i ') ≥ 0 ∀i , i ' d ( j , j ') ≥ 0 ∀j , j ' a) DISTANCIAS DE LA TABLA F(I , J) La expresión general de la distancia en el caso de la comparación de dos elementos líneas de una tabla F(I , J) es la siguiente: d (i ,i ') = nij ni ' j ∑ − n.. n.. J j =1 2 = ( ∑ f ij − f i ' j J j =1 ) 2 ∀i , i ' Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley De la misma manera, la distancia entre dos elementos columnas de una tabla F(I, J) es la siguiente: d ( j , j ') n ij n ij ' ∑ − n.. n.. I = 2 = i =1 ( ∑ f ij− f ij ' J j =1 ) 2 ∀j , j ' b) INDEPENDENCIA ENTRE DOS VARIABLES CATEGÓRICAS: LA DISTANCIA Chi2 Tradicionalmente para determinar si dos variables categóricas son independientes, se usaba la prueba Chi-cuadrado, cuya estadística evalúa globalmente la independencia. Contrasta cada frecuencia relativa conjunta con el producto de sus respectivas marginales, no informa nada respecto a los perfiles sea de fila o columna, de ahí la debilidad de esta prueba. Dos variables categóricas son independientes si, por ejemplo, los perfiles líneas son iguales. En este caso, todos los perfiles líneas son iguales al perfil línea mediano. n n ij = i. n ( =f n ) i = 1, 2, ....., I j = 1, 2, ....., J ) i = 1, 2, ....., I j = 1, 2, ....., J .j .j .. Además podemos decir: n n = ij .j n (= f n i. i. .. Es decir la igualdad de todos los perfiles columnas. En resumen la independencia de las dos variables X e Y puede traducirse por: n ij = nn n i. .j i = 1, 2, ....., I j = 1, 2, ....., J .. O bien de manera equivalente, por: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley f ij = f f i. .j i = 1,2,....., I j = 1,2,....., J Se define el Chi2 de independencia por: nn n ij − i. . j n.. x = ∑∑ nn n 2 2 I J i =1 j =1 i. .j .. Este coeficiente puede interpretarse como el cuadrado de la distancia de la tabla de ni . n. j contingencia observada (nij) y la tabla de independencia n .. Este índice próximo de 0 traduce la independencia de las dos variables. Se puede demostrar que: x 2 =n ( ∑∑ I J i =1 j =1 f ij − f i . f f f i. .j . j ) 2 I = n∑ i =1 ( ) ∑ J j =1 f 2 ij f f i. . j − 1 2 Si planteamos que: θ = xn 2 , el índice θ2 depende únicamente de las frecuencias relativas y no del tamaño n de la población (o de la muestra). 2.2.1.8.- COMPARACION PONDERADA DE PERFILES Cuando aplicamos la distancia entre dos perfiles-línea que hemos definido anteriormente, establecemos la suma de los cuadrados de las diferencias de frecuencias condicionales de cada una de las modalidades de la variable en columna. Llamamos “contribución del atributo j a la comparación de dos perfiles-líneas” al valor de cada termino de esa suma. De la misma Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley manera, llamamos “contribución del atributo i a la comparación de dos perfiles columnas ” al valor de cada termino de la suma de los cuadrados de las diferencias de frecuencias condicionales de cada una de las modalidades de la variable en línea. La importancia de cada elemento de la tabla F, expresada por su frecuencia marginal, la llamaremos en adelante el peso de cada elemento. Para neutralizar la distorsión de la información de la tabla F que persiste cuando comparamos los perfiles de la misma, debemos considerar la “contribución del atributo j (atributo i) a la distancia entre dos perfiles-líneas (columnas)” no ya en valor absoluto, sino en términos relativos al peso del atributo j (atributo i). Procediendo así hacemos que una diferencias entre perfiles sea tanto mas “contributiva” a la relación que queremos establecer entre dos perfiles líneas (columna) cuanto mas raro, menos frecuente, sea el atributo (modalidad) en columna (línea) considerado. Para ello se pondera las contribuciones de cada atributo j (atributo i) a la comparación de dos líneas (columnas) con el valor de la inversa del peso de la columna j (línea i). a) COMPARACIÓN DE PERFILES CON LA DISTANCIA Chi2 Modificando la distancia definida anteriormente entre perfiles, definimos otra expresión de un índice de evaluación de similitudes entre perfiles de una tabla F que respeta la exigencia de comparación que hemos explicado. Ante la desventaja de la prueba Chi-cuadrado se define la distancia Chi-cuadrado entre dos filas (o entre dos columnas) como una distancia euclidiana, al cuadrado, entre sus perfiles, ponderado con las inversas de las frecuencias marginales (MASA) de las columnas. Esta ponderación evita que las columnas más frecuentes tengan más peso en la distancia. En el caso de comparación de dos perfiles líneas i e i’ de F, la distancia entre esos elementos es definida de la siguiente manera: d (i ,i ') = 1 f ij f i ' j ∑ − f f i. f i '. J j =1 .j 2 = 1 f ij f i ' j ∑ − p f i. f i '. J j =1 2 ∀i , i ' ∈ I j Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley En el caso de la comparación de dos perfiles de dos perfiles columnas j e j’ esa distancia es definida de la siguiente manera: d ( j , j ') = f ij f ij ' 1 ∑ − f f . j f . j' I i =1 i. 2 = f ij f ij ' 1 ∑ − p f . j f . j' I i =1 2 ∀j, j ' ∈ J i Esta distancia es llamada “distancia del Chi2 “ o “distancia de Benzecri “ Decimos entonces que la distancia del Chi2 es un índice de evaluación de la información de las tablas de contingencia que neutraliza todas las distorsiones que presentan esa información cuando tratamos de leerla sobre el resumen bruto de una observación: Las tablas T. La menor o mayor distancia entre los puntos indica el grado de similitud o disimilitud entre los perfiles. El objetivo del AC es reducir la dimensión de estos espacios para facilitar la interpretación del grado de similitud de las distintas categorías. Importante: Se puede analizar los perfiles fila o los perfiles columna, ambos planteamientos producen los mismos resultados, filas y columnas juegan un papel simétrico en el análisis. b) PROPIEDAD DE EQUIVALENCIA DISTRIBUCIONAL Estas distancias tienen la PROPIEDAD DE EQUIVALENCIA, Benzécri (1963). Brevemente, este principio establece que: Si dos filas son idénticas (equivalencia distribucional), entonces esas dos filas de la tabla de contingencia original pueden juntarse en una sola fila, sin afectar la geometría de los perfiles columna. Lo mismo ocurre con las columnas. Podemos formular esta propiedad de la siguiente manera : Si dos líneas (o columnas) de una tabla de contingencia son proporcionales (es decir que presentan el mismo perfil), se las puede remplazar por una sola línea (o columna), suma de las dos líneas (o columnas) proporcionales, sin que esto altere las distancias relativas de los puntos-columnas(o líneas) en el espacio de representación correspondiente. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 2.2.1.9.- REPRESENTACIÓN EN TERMINOS DE INERCIA DE UNA NUBE DE PUNTOS Una tabla de contingencia puede ser leída sin distorsiones si expresamos esa información por medio de: • Dos espacios euclidianos de representación de los perfiles asociados a la tabla, dotado de sus respectivos pesos. • Un índice de evaluación de la similitud entre perfiles ponderados asociados a la tabla F (o la tabla T), que llamamos distancia del Chi2 . Ahora bien, puesto que la representación analógica de la información se presenta ahora bajo la forma de una cierta distribución de masas en dos espacios euclidianos, no podemos “leer” en ello la forma de la información de la tabla F, o la tabla T, en términos de la posición relativa de punto-perfiles, puesto que el peso asociado a esos puntos modifica sus posiciones relativas. Evocando el concepto físico de inercia veremos que la forma de la información de la tabla F debe ser leída ahora en términos de dispersión de esos puntos masas con respecto a un punto de referencia. a) INERCIA DE UNA NUBE DE PUNTOS CON REPECTO A UN PUNTO DE REFERENCIA Llamamos inercia de una nube puntos perfiles N(I) dotados de pesos con respecto a un punto cualquiera m, a la dispersión de esa nube de puntos con respecto al punto m tomado como referencia. Sea un conjunto de puntos definido así: I = (1, 2, 3, ...........I), dotados de pesos, pI = (p1 , p2 , p3 , ............pI), que llamamos nube de puntos N(I). En esta figura, esos puntos están ubicados en el espacio mediante sus coordenadas en los ejes α y β. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley FIGURA II β p1 mβ m D(I , G) 1β .1 .2 .I .3 .i p3 Pi mα p2 pI α 1α La dispersión de esa nube de puntos con respecto a un punto m cualquiera de ese espacio esta evaluada por la expresión siguiente: I Im=∑ i =1 2 p d( i i, m) ∀i ∈ I Decimos entonces que la inercia, con respecto a m, de una nube de puntos N(I) es igual a la suma de los productos del cuadrado de la distancia a m de cada punto de la nube multiplicada por el peso asociado a cada punto. Llamamos contribución del punto i a la inercia con respecto a m de la nube de puntos N(I) al termino correspondiente del punto i en esa suma. La contribución del punto i a la inercia con respecto a m de la nube de puntos es definida así: Contribucion I ( i ) = p d m i 2 ( i ,m ) ∀i ∈ I Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Consideremos ahora el mismo sistema de masas en un plano y veamos la dispersión de esos puntos con respecto a un punto particular del plano: El punto en torno ala cual esas masas están en equilibrio. Decimos que esos puntos están en equilibrio en torno al punto G por que consideramos que la rotación del sistema de masas en torno a G es nula. Como vemos en el siguiente grafico: FIGURA III P2 β 1β P1 D(i , G) .2 .1 Gβ G .I .3 .i pI P3 Pi Gα 2α α Los tres puntos ubicados a la derecha del punto G imponen una cierta cantidad de movimiento (en el sentido señalado por la flecha que parte del punto i) que se compensa, teniendo en cuenta los pesos relativos de esos puntos con el movimiento (en el sentido señalado por la flecha que parte del punto 3) impuesto por los dos puntos ubicados a la izquierda de G, tomando en cuenta sus pesos relativos. Definiendo así la condición de equilibrio de ese sistema de masas, diremos que el punto G es el centro de gravedad del sistema, o bien el punto baricentro. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley S i G es el centro de gravedad del sistema, una fuerza impuesta en G (paralela a las fuerzas que representan los pesos de cada punto del espacio pero de sentido contrario) y de magnitud igual a la suma de los pesos de cada punto del espacio, mantiene el sistema de punto “suspendido” en el espacio, sin alterar la forma del sistema de masas. S i el punto G es el baricentro del sistema de masas, las coordenadas de G sobre cada eje del referencial de ese espacio es igual a la media ponderada de las coordenadas de los puntosmasa en el mismo referencial. Llamando “Inercia” esa dispersión, así evaluada, de los puntos de N(I) con respecto a un punto m cualquiera “evocamos” el concepto físico de “cantidad de movimiento” de un conjunto de masas en torno a un punto de referencia. Sin embargo no podemos considerar que la dispersión de puntos dotados de masas en los espacios de representación que hemos creado, cumplen con las mimas leyes, formuladas en física, que rigen los equilibrios de masas reales. b) INERCIA DE LOS PUNTOS PERFILES PONDERADOS CON RESPECTO A LOS CENTROS DE GRAVEDAD b.1) INERCIA DE LOS PUNTOS PERFILES LINEAS PONDERADOS (N(I)): La contribución de la fila i a la inercia de la nube de puntos N(I) con respecto a GI es definida así: 2 ( i ) = p ContribucionI i d ( i ,G ) ∀i ∈ I I GI La inercia de las nubes N(I) con respecto a GI es entonces igual a la suma de las contribuciones a esa inercia de todas las filas: I IG I (N ( I ) ) = ∑ p i d 2( i ,G i =1 I ) ∀i ∈ I Por otra parte, sabemos que las coordenadas del punto i en el espacio de representación de los puntos perfiles fila dotados de pesos son las siguientes: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley f f i1 f 1. , .1 f f i2 f 2. , .......... , .2 f f iJ f i. .J Las coordenadas del punto GI en ese mismo espacio de representación son las siguientes: f f .1 f f , .1 .2 f f , .........., .2 = .J .J [ f .1 f , .2 f , ..........., .J ] b.2) INERCIA DE LOS PUNTOS PERFILES COLUMNAS PONDERADOS (N(J)): La contribución de la columna j a la inercia de la nube de puntos N(J) con respecto a GJ es definida así: 2 ( j ) = p Contribuci on I j d ( j ,G GJ J ∀j ∈ J ) La inercia de las nubes N(J) con respecto a GJ es entonces igual a la suma de las contribuciones a esa inercia de todas las columnas: J I G (N ( J ) ) = ∑ p d j =1 J j 2 G) ( j, ∀j ∈ J J Por otra parte, sabemos que las coordenadas del punto j en el espacio de representación de los puntos perfiles columna dotados de pesos son las siguientes: f f .1 1j f , 1. f f .2 2 j f , .......... 2. f f .j Ij f I. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Las coordenadas del punto GJ en ese mismo espacio de representación son las siguientes: f f 1. f f , 1. 2. f f , .........., 2. = I. I. [ f 1. f , 2. f , ..........., ] I. b.3) LOS PUNTOS PERFILES MARGINALES G SON LOS BARICENTROS DE LAS NUBES DE PUNTOS N(I) Y N(J) Las coordenadas de los puntos perfiles columnas en el eje i del referencial de ese espacio son las siguientes: f f 1. i1 f , .1 f f i2 f 2. f , .......... , f .2 iJ f i. .J De modo que la media ponderada por el peso de esos perfiles de esas coordenadas es la siguiente: X= ∑ n . j n.. j =1 1 f J f .j ij J 1 J = ∑ n. j ∑ f i. n.. j=1 j =1 J f f .j = ij f f ∑ f f J 1 j =1 i. i. ij = .j ∑f 1 j =1 ij J f ∑f i. j =1 .j = f f i. = i. Vemos que la media ponderada de las coordenadas de los puntos-perfiles columnas sobre el eje i es igual a la coordenada del perfil marginal en columna sobre ese mismo eje. Las coordenadas de los puntos-perfiles línea en el eje j del referencial de ese espacio son las siguientes: f f .1 1j f , 1. f f .2 2 j f , .......... 2. f f .j Ij f I. Siendo la media ponderada de esas coordenadas: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM f i. Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 1 I X= ∑ n i. n .. i=1 f f i. ij f .j I 1 I = ∑ ∑ ni. i=1 n .. i =1 I f f i. f f ∑f f I 1 = ij ij i =1 .j = i. .j ∑f 1 i =1 I ij i =1 i. f ∑f .j = f f .j = .j Vemos también que la media ponderada de las coordenadas de los puntos perfiles línea sobre el eje j es igual a la coordenada del perfil marginal en línea sobre ese mismo eje. De modo entonces que el punto perfil marginal G de cada uno de esos espacios de representación es el baricentro de esas nubes de puntos. 2.2.1.10.- REPRESENTACIÓN FACTORIAL DE LA INFORMACION DE UNA TABLA DE CONTINGENCIA a) LOS FACTORES DE UNA NUBE DE PUNTOS-PERFILES: Las coordenadas de los puntos perfiles (en línea y en columna) en el nuevo referencial se obtienen por simple proyección ortogonal de los puntos-perfiles (centrados en G) sobre las rectas del nuevo referencial de cada espacio. Esas coordenadas están definidas así: J F α (i ) = ∑ Z j U α j j =1 I y Gα ( j ) = ∑ K iW αi i =1 Decimos entonces que: F1 (i) es la coordenada de la i- esima línea de la tabla T sobre el primer eje factorial; F2 (i) es la coordenada de la -i esima línea de la tabla T sobre el segundo eje factorial; etc... Por otra parte, G1 (j) es la coordenada de la j-esima columna de la tabla T sobre el primer eje factorial; G2 (j) es la coordenada de la j- esima columna de la tabla T sobre el segundo eje factorial; etc... b) PROPIEDADES DE FACTORES DE LAS NUBES DE PUNTOS-PERFILES (INDICES DE AYUDA A LA INTERPRETACION) b.1) COORDENADAS DEL CENTRO DE GRAVEDAD Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM f .j Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Los centros de gravedad de las nubes de puntos N(I) y N(J), respectivamente, están ubicados por construcción, en el origen de esos nuevos sistemas de ejes de referencia que son los factores de esas nubes de puntos-perfiles. En consecuencia sus coordenadas de sus espacios factoriales de representación son nulas. Es decir: F (G ) = 0 α L ∀α = 1, 2, ......, p G (G ) = 0 y α C ∀α = 1, 2, ......, p Sabemos que las coordenadas del centro de gravedad de una nube de puntos-perfiles se obtienen haciendo la media (ponderada por el peso asociado a cada punto de la nube) de las coordenadas de los puntos de la nube. Lo cual podemos expresar de la siguiente manera: ∀i ∈ I y ∀α , ∑ f F (G ) = 0 = ∑ f G (G ) I J i. i =1 α L j =1 .j α ∀j ∈ J y ∀α C De modo entonces que los “factores” de las nubes de puntos-perfiles constituyen una serie de p variables (cuantitativas, a valores de R) de media nula, es decir una serie de p variables centradas. b.2) VARIANZA DE LOS FACTORES DE UNA NUBE DE PUNTOS-PERFILES Considerando las variables cuantitativas que llamamos “factores” de una nubes de puntosperfiles, podemos calcular la varianza de las mismas. _ Tratándose de variables centradas, hemos visto que S 2 α I =∑ i =1 X α =0 p (xαi − x α) = ∑ p (F α(i )− 0) = ∑ p (F α(i )) 2 i I i =1 2 i I i =1 2 i ∀α = 1, 2, ......, p En esa expresión: Fα(i) es la coordenada del punto i sobre el eje α, es decir la distancia del origen del eje (que corresponde al centro de gravedad GL) de la proyección ortogonal del punto i sobre el eje α; y pi es peso asociado al punto perfil i. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley De modo que la varianza del factor α es igual a la inercia de la nube de puntos N(I) a lo largo de ese eje. Pero se puede verificar (y demostrar) que la inercia a lo largo de cada eje factorial de una nube de puntos-perfiles esta dada por el valor propio asociada a cada eje. Podemos entonces establecer la relación siguiente: S 2 α I = λα = ∑ i =1 p (F α(i)) 2 i ∀α = 1, 2, ......, p b.3) VALORES PROPIOS PERTINENTES DE UN ANÁLISIS Si un valor propio es muy pequeño (próximo a cero), concluimos que la parte de la asociación observada entre las variables de la tabla de contingencia que es asumida por el eje correspondiente es ínfima. El complemento de información que aporta ese eje a la in formación de representación global de la tabla es insignificante o despreciable. En la practica del empleo de este método de análisis, sobre tablas de contingencia de grandes dimensiones, el valor propio limite puede ser fijado calculando el valor propio medio. Es decir que: λ= I G ( N (I )) ; L p I o bien λ = G C (N ( J ) ) p No debemos utilizar esta regla de manera absoluta cuando procedemos a la interpretación de los resultados de un análisis. Si se analiza, por ejemplo, una tabla de contingencia de grandes dimensiones cuya inercia global no sea muy elevada, el valor propio medio será ya muy próximo a cero. Los valores propios próximos precedentes pueden también ser casi nulo, es decir que aportan una información complementaria que es ya despreciable. La traza de la matriz inercia de una nube puntos-perfiles es la medida de la inercia global de esa nube de puntos con respecto al centro de gravedad de la misma. La inercia global de esa nube de puntos con respecto al centro de gravedad, es igual al índice ϕ2 de asociación de las variables que componen la tabla de contingencia. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley p De modo que: I G = ∑ λα = ϕ 2 α =1 b.4) TAZA DE INERCIA DE UN FACTOR Sabiendo que la inercia IG de la nube de puntos-perfiles N(I) (o N(J)) es igual a la suma de los p valores propios λα no nulos, podemos expresar el aporte de cada eje a la inercia total de la nube por medio del índice τα , que expresa la taza de inercia del factor y que definimos a continuación: τ α = λ ∑λ × 100 = λα × 100 α p I α α =1 G Siendo, claro esta: p ∑τ α =1 α = 100% b.5) TAZA DE INERCIA DE UN PLANO FACTORIAL: Si nos interesamos en la inercia de una nube de puntos perfiles proyectada sobre un plano definido por dos ejes factoriales α i y α i+k , sabemos que la inercia de la nube sobre ese plano esta medida por: λαi + λα(i+k) (puesto que el eje α i al eje α i+k ), de modo que la taza de inercia asociada al plano (i , i+k) es definida así: τ = plano ( i , i+ k ) (λα λα ) ×100 i+ k i p ∑λ α =1 α La taza de inercia expresa la parte de inercia global que es representado a lo largo de un eje factorial o sobre un plano factorial. Pero el índice ϕ2 de asociación entre las variables que Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley sirve de referencia al índice τα , no constituye una medida significativa de la información que aporta la tabla de contingencia. b.6) CONTRIBUCION DE LOS PUNTOS PERFILES A LA INERCIA A LO LARGO DE UN EJE FACTORIAL Contribución del punto i al eje α : p (F α(i)) × 100 CTR (i) = λ i α ∀i ∈ N ( I ) α Contribución del punto j al eje α : CTR ( j ) = α p (Gα( j)) × 100 λ j ∀j ∈ N ( J ) α La contribución de un punto-perfil a la inercia de un factor es un índice que juega un rol determinante cuando se trata de interpretar los resultados del análisis de la información aportada por una tabla de contingencia. La contribución de un punto-perfil conjuga el peso y la coordenada ligados a cada punto. Esto permite evitar los errores de interpretación que produciría una lectura “inocente” de los gráficos de los ejes factoriales que tome en cuenta solamente las coordenadas de los puntosperfiles, olvidando que cada punto tiene asociado un peso (no representado) y que el objetivo del grafico del eje factorial es rendir cuenta de una parte de la inercia global de la nube de puntos-perfiles. b.7) CALIDAD DE REPRESENTACIÓN DE LOS PUNTOS PERFILES Podemos entonces expresar por medio de un índice de calidad de representación del punto en cada eje, la parte de la distancia de un punto i (o del punto j) al centro de gravedad, que es representada por la coordenada del punto i (o del punto j)sobre cada eje factorial. Calidad de representación del punto i sobre el eje α : Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley ( (i) ) (i ) = F α 2 COR α d ∀ α = 1, 2, ......, p 2 p Siendo : ∑ COR α (i ) = 1 ∀i ∈ N ( I ) α =1 (i ,G ) Calidad de representación del punto j sobre el eje α : ( ( j) ) ( j ) = Gα 2 COR α d 2 ∀α = 1, 2, ......, p ( j, G) p Siendo : ∑ COR α ( j ) = 1 ∀j ∈ N ( J ) α =1 S i un punto-perfil i presentara un CORα(i) = 100% para un eje α dado, esto significa que el eje α “representa” perfectamente el punto perfil i puesto que Fα(i) = d(i , 0) . Decimos entonces que el punto perfil i esta completamente “explicado” por el eje α. Considerando solamente ese eje, podemos explicar completamente la posición del punto i con respecto a todos los otros puntos-perfiles de la nube N(I). En cambio, si un punto-perfil i presentara un CORα(i) = 0% para un eje α, esto significa que Fα(i) = 0, es decir que ese punto esta situado en un sub-espacio ortogonal al eje α. Ese eje no esta asociado a ese punto. De modo entonces que el coeficiente CORα(i) (CORα(j)) se interpreta como un coeficiente de correlación múltiple entre cada variable de la tabla T y el conjunto de p variables factoriales construidas por el Análisis Factorial de Correspondencias de la tabla T. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 2.2.2.- ANALISIS DE CORRESPONDENCIAS MÚLTIPLES El análisis Factorial de Correspondencias Múltiples es un instrumento de investigación interesante cuando se trata de analizar la información aportada por tablas de contingencia de grandes dimensiones. Pero pocas son las áreas de investigación en ciencias humanas en las cuales se hace uso de ese tipos de tablas. En efecto muy a menudo los investigadores proponen estrategias de observación de una población dada (conjuntos de unidades de observación), a fin de relevar sobre ese conjunto numerosas características, cada una de ellas compuesta de un pequeño numero de modalidades. Por medio “Encuestas”, se elaboran tablas que resumen las p características observadas sobre n unidades de observación. El análisis Factorial de Correspondencias Múltiples es un instrumento particularmente adaptado al tratamiento estadístico de los datos producidos por esos tipos de observaciones. Este método de análisis estadístico responde a la doble exigencia de objetividad en ese proceso de reducción y de exploración de lo observado y de tratamiento de la información con el nivel de síntesis de lo adecuado al cuadro conceptual utilizado. El análisis Factorial de Correspondencias Múltiples responde a esa exigencia metodológica de analizar la información aportada por la observación de diferentes dimensiones cualitativas u ordinales de una población, respetando el nivel de síntesis que impone el cuadro conceptual con el cual el investigador concibe su problemática de estudio y diagrama el dispositivo de observación. Esta adecuación metodológica del Análisis Factorial de Correspondencias Múltiples explica su rápida difusión en diferentes campos de investigación en ciencias humanas, como también el hecho que el método del Análisis Factorial de Correspondencias Binarias es empleado solamente en ciertos sectores de investigación que elaboran regularmente tablas de contingencia de grandes dimensiones. Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley 2.2.2.1.- TABLAS DE CONTINGENCIA MÚLTIPLE DE ESTADÍSTICAS DE RESUMEN DE LO OBSERVADO a) TABLA DE CODIGOS CONDENSADOS Presentamos aquí el modelo general de una tabla de códigos condensados y las principales características de las mismas: TABLA DE CODIGOS CONDENSADOS TCC(n , p) Individuo 1 2 . . . i . . . n 1o 1 2 . . . ki1 . . . kn1 Código de la característica 2o (…) j-esima (…) p-esima 2 … 2 … 4 1 … 1 … 3 . . . . . . . . . . . . . . . ki2 … kij … kip . . . . . . . . . . . . . . . kn2 … knj … knp En esta tabla cada línea contiene todos los códigos correspondientes a las modalidades atribuidas a un individuo para cada una de las características observadas. En una tabla TCC(n , p), en la intersección de la i- esima línea y de la j- esima columna figura el valor kij , es decir el código numérico que fue dado a la modalidad “atribuida” al -i esimo individuo a propósito de la j-esima característica observada. De modo que podemos leer lo resumido en esa tabla de la siguiente manera: El i-esimo individuo presento la modalidad codificada kij de la j-esima característica... Tratándose de una tabla de códigos la tabla TCC(n , p) no posee propiedades numéricas. Las sumas en líneas y en columnas de los valores de la misma (márgenes de tabla) no tienen sentido. b) TABLAS LOGICAS A partir de una tabla de códigos condensados podemos generar una tabla numérica capaz de resumir la misma información. Conoceremos la primera columna de la tabla TCC(n , p) que presentamos anteriormente. Esa columna nos permite asociar a cada individuo de la muestra Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley (y solo una) una modalidad de la primera características observada. Podemos asociar a esa columna una tabla que, para cada individuo de la muestra, indique cual es la modalidad de esa característica que le fue atribuida. Presentamos a continuación la tabla asociada a esa columna: TABLA TCC(n , 1) Correspondiente a la primera columna de la tabla TCC(n , p) Individuos 1 2 . . . i . . . n Código de la Primera Característica Observada 1 2 . . . ki1 . . . kn1 TABLA TL(n , 3) Asociada a la primera columna de tabla TCC(n , p) Individuo 1 2 . . . i . . . n Modalidades de la primera característica observada Codigo Codigo Codigo 1 2 3 1 0 0 0 1 0 . . . . . . . . . 0 xi1 0 . . . . . . . . . 0 0 xn1 1 1 . . . 1 . . . 1 Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley En la tabla TL(n , 3) asociada a la primera columna de la tabla TCC(n , p): xi1 = 0 , si y solo si ki1 = 2 ⇒ xi1 = 1 xn1 = 0 , si y solo si kn1 = 2 ⇒ xn1 = 1 De modo que, si al i- esimo individuo le corresponde, en la tabla TCC(n , p), el valor código de modalidad “2” en la primera característica observada, la tabla asociada a esa columna indica que el i-esimo individuo presentó esa modalidad para esa característica, dando el valor 1 al segundo elemento de la i-esima línea y dando el valor cero a los otros dos. A la primera columna de la tabla TCC(n , p) le hemos asociado así una tabla TL(n , 3) por que esa primera columna de la tabla TCC(n , p) comporta tres modalidades mutuamente exclusivas. La tabla TL(n , 3) contiene las tres “variables indicadoras” de las modalidades de la primera característica observada. Esas variables afectan, a cada modalidad de la primera característica observada: el valor 1 al i- esimo individuo si este presento esa modalidad; y el valor 0 si el iesimo individuo no presento esa modalidad. Esas variables son llamadas también “variables de presencia-ausencia” de una modalidad dada. Notemos también, que el margen inferior de la tabla TL(n , 3) corresponde a la distribución de frecuencias de la primera característica observada en la muestra de n individuos. El margen derecho de esa tabla es constante e igual a 1. Si repetimos esa operación para cada columna de la tabla TCC(n , p), podemos asociar a ella una tabla TL(n , k), es decir una tabla de tantas variables indicadoras como modalidades presenten las p características que configuran la tabla TCC(n , p). Se construye así la tabla lógica correspondiente a la tabla TCC(n , p): Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley TABLA LOGICA TL(n , k) Correspondiente a la tabla TCC(n , p) Individuos 1 2 3 . . . i . . . n Margen 1 racaracteristica Modalidades 1 (…) 0 … 1 … 0 … . . . 0 … . . . 1 … n1 1 … 0 … 1 … . . . 1 … . . . 0 … … k1 0 0 0 . . . 0 . . . 0 n k1 … j-esima característica Modalidades … … … … . . . … . . . … … Kj-1 +1 (…) k j-1 +k j 1 … 0 … 0 … 0 … 0 … 1 … . . . . . . 0 … xij … . . . . . . 0 … xnj … n ((Kj-1)+1) … 0 1 0 . . . 0 . . . 0 n Kj-1+Kj … … … … … . . . … . . . … … p-esima característica Modalidades Kp-1 +1 (…) 1 … 0 0 … 1 0 … 0 . . . . . . 1 … 0 . . . . . . 0 … 1 N((Kp-1)+1) k … 0 … 0 … 1 . . . … 0 . . . … 0 … nK Margen P P P . . . p . . . p np Siendo K =ΣKm el total de modalidades de las p características observadas. Las K columnas de la tabla T(n , k) son las variables indicadoras de las K modalidades de las p características observadas. De modo entonces que la suma en línea de esa tabla define un margen constante, igual a p. Cada bloque de variables indicadoras correspondiente a una característica define, por suma en columna, un margen que corresponde a la distribución de frecuencias brutas de la características. De modo que el margen inferior de la tabla TL(n , k) expresa la distribución de frecuencias brutas de todas las características observadas. La suma de sus márgenes es, evidentemente, igual a np. Una tabla TL(n , k) es una tabla de correspondencia de tipo particular que resulta de la yuxtaposición de las tablas de presencia-ausencia correspondiente a cada característica considerada en el estudio. 2.2.2.2.- ANÁLISIS FACTORIAL DE CORRESPONDENCIAS DE UNA TABLA LOGICA TL(n , k): a) OBJETIVOS DEL ANÁLISIS Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley • El primer objetivo específico del Análisis Factorial de Correspondencias Múltiples es de facilitar la construcción de esas tipologías de individuos permitiendo la comparación de todas las unidades de observación a través de todas las modalidades de las características observadas . Para obtener una representación grafica de esas comparaciones, debemos de definir un espacio de representación de los individuos cuyo referencial sean las K modalidades consideradas en las p características observadas. Como un espacio de representación esta definido por la distancia entre los elementos que lo caracterizan, debemos dotarnos de una distancia euclidiana entre los individuos. La distancia propia ha ese espacio debe corresponder con el siguiente criterio de comparación: Dos individuos que presentaron un gran numero de modalidades en común deben ser incluidos en una misma clase de la tipología de individuos. • El segundo objetivo específico del Análisis Factorial de Correspondencias Múltiples es estudiar la relación existente entre las características observadas. • El tercer objetivo específico del Análisis Factorial de Correspondencias Múltiples es resumir el conjunto de características observadas en un pequeño numero de variables cuantitativas relacionadas con el conjunto de variables cualitativas estudiado. • El cuarto objetivo específico del Análisis Factorial de Correspondencias Múltiples es permitir la comparación de modalidades de las características observadas. b) DISTANCIA ENTRE INDIVIDUOS (LINEAS) DE UNA TABLA LOGICA El cuadrado de l distancia del Chi2 entre los puntos de individuos i e i’ esta dada por la suma de los cuadrados de las diferencias de coordenadas, es decir que: d 2 ( i ,i ' ) = K x ij x i' j − ∑ j=1 nj p nj p np np 2 = x ij x i ' j − ∑ j=1 n j p p K np 2 = 1 p K n j =1 nj ∑ (x ij − x i ' j ) 2 La distancia entre los puntos i e i’ queda entonces definida de la siguiente manera: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley d (i ,i ') = np xij x i' j ∑ − n p p 2 K j =1 j = 1 K n ∑ p j =1 n j (x ij − x i' j ) 2 Cuando se calculan todos los términos de la sumatoria que establece las distancias entre dos individuos i e i’, es evidente que la distancia entre los mismos crece a medida que aumentan las diferencias de modalidades presentadas por los individuos i e i’. Cuando dos individuos divergen a propósito de modalidades raras (de bajo peso), la distancia entre los mismos será mas grande que en el caso en que los mismos individuos presenten el mismo numero de divergencias, pero a propósito de modalidades muy frecuentes (de gran peso). De modo entonces que la distancia Chi2 entre individuos de una tabla lógica respeta el criterio de comparación de individuos que hemos adoptado. c) DISTANCIA ENTRE MODALIDADES (COLUMNAS) DE UNA TABLA LOGICA Sean por ejemplo dos modalidades j y k de la tabla lógica TL(n , k), sus coordenadas en el referencial de los individuos son los siguientes: x1 j x2 j xij xnj np np np np Modalidad j : ; ; .....; ;.....; nj p nj p nj p nj p np np np np np np np np x1k x x x 2k ik nk np np np np Modalidadk : ; ; .....; ;.....; nk p nk p nk p nk p np np np np np np np np Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley De modo que el cuadrado de la distancia entre esas dos modalidades (tratándose de un espacio euclidiano) esta definido así: xij xik x np np ij x ik = n xij x ik = ∑ = − − ∑ − n j 1 nk 1 ∑ 1 1 n j nk nk nj n n np n np n 2 2 2 d 2 ( j ,k ) n n n i =1 i =1 i =1 La distancia Chi2 entre dos modalidades es entonces la siguiente: d 2 ( j, k ) = xij xik ∑ n − n j nk 2 n i =1 Desarrollando esa expresión podemos mostrar claramente la significación de la distancia entre dos columnas de la tabla lógica. Podemos escribir esa expresión de la siguiente manera: x2ij n 2 + d ( j, k ) = ∑ n i =1 j 2 n 2 x n ik 2 k −2 x x n n ij j k ik d) INERCIA TOTAL CON RESPECTO AL CENTRO DE GRAVEDAD DE LA NUBE DE PUNTOS N(J) Calculemos en primer lugar la contribución de un modalidad a la inercia global de la nube de puntos N(J): En el caso de una tabla de contingencia, hemos visto que la contribución de la j-esima modalidad a la inercia global con respecto al centro de gravedad GC esta definida de la siguiente manera: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Contribuci on I ( j ) = p d j GC ∀j ∈ J 2 GJ) ( j, Tratándose de una tabla lógica, la contribución de la j- esima modalidad a la inercia global con respecto al centro de gravedad GC es definida así: Contribuci on I ( j ) = p d j GC ∀j ∈ J 2 GC ) ( j, Calculemos el cuadrado de la distancia de la j-esima modalidad al centro de gravedad GC: d x ij 1 np = ∑ − nj 1 n np n 2 n 2 G ( j, C ) i =1 1 x ij = ∑ − n 1 nj n n i =1 2 x ij 1 = ∑ n n −n j 2 n i =1 Desarrollando el termino entre paréntesis obtenemos que: xij 1 − nj n 2 n d ( j ,G ) = ∑ i =1 n 2 C La inercia global con respecto a GC de la nubes de puntos N(J) es definida así: K ∑ Contribuci j=1 on I ( j) = G C K ∑ j=1 1 p 1 − = n n j K ∑ j=1 1 − n j np P = K ∑ j=1 1 − p n ∑ np K j j =1 Es decir que: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley IG C ( N ( J )) = K −1 p De modo entonces que la inercia global de la nube de puntos N(J) de una tabla lógica no depende mas que del numero de características observadas (p) y del numero total de modalidades que presentan esas características (K). decimos entonces que la inercia global de una tabla lógica no depende mas que de su “forma”. 2.2.2.3.- TABLA DE BURT (ANEXO III) La tabla de Burt TB(K , K) es una tabla simétrica que presenta el conjunto de las tablas de contingencia que pueden ser construida cruzando dos a dos las p características observadas. Si llamamos, como en el caso de la tabla lógica, K la suma de las modalidades de la p características observadas sobre los n individuos, la tabla de Burt presenta: • A la intersección de la j-esima línea y la j-esima columna, el valor njj es decir el numero de individuos que presentaron la j-esima modalidad de una característica dada. • A la intersección de la j- esima línea y de la k-esima columna, el valor njk = 0 si la jesima modalidad y la k-esima modalidad pertenecen a una misma característica observada. • A la intersección de la p-esima línea y de la k-esima columna, el valor nqk , es decir el numero de individuos que presentaron, simultáneamente, la p-esima modalidad de una característica dada y la k-esima modalidad de otra característica observada. Tratándose de una tabla simétrica, construida con la yuxtaposición de todas las tablas de contingencia definidas por las p características observadas (tomadas dos a dos) de todas las variables cualitativas contenidas en ella. La diagonal de la tabla TB(K , K) esta constituida por la distribución de frecuencias brutas de todas las modalidades, de todas las variables cualitativas que componen la tabla. a) ANALISIS FACTORIAL DE CORRESPONDENCIAS DE UNA TABLA DE BURT Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Considerando la tabla TB(K , K) como una tabla de correspondencias, la información aportada por esta tabla TB(K , K) resulta de la comparación de todas las modalidades que la constituyen. Es necesario entonces, definir el criterio de comparación con el cual debemos tratar la información de dicha tabla. Cada variable cualitativa realiza una partición de los n individuos observados en tantas clases como modalidades constituyan la variable. Dos clases dadas (dos modalidades) serán consideradas cuando presenten distribuciones de frecuencia equivalentes de las variables cualitativas consideradas. Dicho de otra manera, dos clases de individuos serán semejantes cuado presenten perfiles equivalentes de distribución del conjunto de variables cualitativas consideradas. Podemos definir un espacio euclidiano de representación de la información aportada por una tabla de Burt. Representamos los puntos-perfiles ponderados de las k modalidades de la tabla en un referencial de k dimensiones. Dotando ese espacio de la distancia Chi2 entre modalidades, se puede verificar que respeta el criterio de comparación de las mismas que hemos adoptado. Tratándose de una tabla simétrica, la representación de una sola de las dos las nubes de puntos perfiles ponderados N(I) o N(J) es suficiente para representar toda la información contenida en una tabla de Burt. La distancia del Chi2 entre dos modalidades i e i’ esta definida entonces de la siguiente manera: n n ij n ni' j =∑ p × n i.n. j − p × n i'.n. j 2 d 2 (i ,i ' ) K j =1 1 K n n ij ni ' j = ∑ × − p j =1 n. j n n 2 i. i '. Expresando esa distancia en términos de perfiles-ponderados, la distancia del Chi2 entre dos líneas i e i’ de una tabla de Burt queda definida de la siguiente manera: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley f ij f i' j 1 1 × ∑ f − f p p f i. i '. 2 K d (i ,i ') = 2 j =1 .j Centrando ese espacio de representación en el centro de gravedad de esa nube de puntosperfiles ponderados, y calculando la matriz de inercia de la nube centrada de puntosmodalidades, podemos determinar sus direcciones principales de alargamiento y definir un nuevo referencial de representación: los ejes factoriales. El análisis factorial de Correspondencias de una tabla de Burt produce una buena representación grafica de la información aportada por dicha tabla. b) COEFICIENTES DE AYUDA A LA SELECCION DE EJES FACTORIALES b.1) VALORES PROPIOS Estudiando la relación entre una variable cualitativa y un eje factorial, sabemos: n k − k j − 1+ k j (G α , j ) = p K = ∑ + 1 k j −1 2 p G k 2 α ( ) j k ∀ j = 1, 2 , . . . . . , p Entonces los valores propios de un Análisis Factorial de Correspondencias Múltiples, están comprendidos en el intervalo [0 , 1] . Si: λ α 1 = p p ∑ n (G j =1 2 α ,j , cuando ) se v e r i f i c a q u e : λ α 2 n (G α ,j )= 1 ∀ j = 1,2,....., p =1 b.2) TAZA DE INERCIA DE UN FACTOR La taza de inercia de un factor no es mas que una proporción cuyo denominador carece de significación en términos de “información total” aportada por la tabla: τ α = λ ∑λ α p α =1 α × 100 = λα I G Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Los valores propios y las tazas de inercia de los ejes factoriales que resulta del Análisis Factorial de Correspondencias Múltiples de una tabla de “individuos-variables cualitativas” no son índices de naturaleza tal que permitan decidir la importancia relativas de los ejes factoriales. En cambio, el diagrama de la taza de la inercia de los valores propios no nulos pueden darnos ciertas indicaciones generales que permiten hacer una primera selección indicativa del numero de ejes factoriales “interesantes” que merecen ser considerados. El diagrama de la taza de inercia de los primeros valores propios no nulos resultantes de la descomposición de la inercia global de una tabla lógica (o de la tabla de Burt correspondiente) presenta la forma de una curva en S, cuyo punto de inflexión se procesa en torno a la taza de inercia correspondiente al valor propio “medio”, el cual es definido así: p − λ= ∑λ I = i i =1 p G p En situación de independencia (nube de puntos-modalidades de forma esférica) la descomposición de la inercia global de una tabla lógica produce una serie de valores propios que presentan un decrecimiento regular. La forma del diagrama de la taza de inercia de dichos valores propios es entonces una curva en S regular. Vemos entonces que, aunque los valores propios y las tazas de inercia de los factores no son índices aptos para seleccionar los ejes factoriales que deben ser interpretados, el diagrama de las tazas de inercia de los factores nos permiten identificar las principales deformaciones de las nubes de puntos-modalidades y en consecuencia hacer una primera selección indicativa de los factores que merecen ser analizados en la etapa de interpretación de resultados de un Análisis Factorial de Correspondencias Múltiples. c) COEFICIENTES DE AYUDA A LA INTERPRETACION DE LOS EJES FACTORIALES c.1) ESTUDIO DE LOS EJES FACTORIALES EN RELACION CON LAS VARIABLES: Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM Aplicación del Análisis Factorial de Correspondencias a Mapas Perceptuales de los pacientes Infectados por enfermedades de Transmisión Sexual. Chumpitaz Ramos, Domingo Derechos reservados conforme a Ley Los programas de aplicación editan no solamente las contribuciones la inercia a lo largo de cada eje factorial del conjunto de modalidades presentes en la tabla lógica (o en la tabla de Burt) estudiada, si no también la suma de esas contribuciones para el conjunto de modalidades de una misma variable cualitativa. De modo entonces que los programas de aplicación aportan los elementos necesarios para el calculo del índice de correlación n2 entre cada variable cualitativa de la tabla y cada eje factorial . c.2) CONTRIBUCION DE LOS INDIVIDUOS Y DE LAS MODALIDADES A LA INERCIA A LARGO DE UN EJE FACTORIAL: GRADO DE GENERALIDAD DE UN EJE FACTORIAL En el caso del Análisis Factorial de Correspondencias Múltiples de una tabla lógica, los programas de aplicación calculan y editan las contribuciones de los puntos-individuos y de los puntos-modalidades a la inercia proyectada a lo largo de los ejes factoriales. Las contribuciones de esos elementos son definidas de la siguiente manera: 1 CRT α (i) = n ( Fα(i )) ×100 n 2 λ α .j ∀i ∈ N( I ) ; CRT α ( j ) = n (Gα( j )) ×100 2 λ ∀j ∈ N(J ) α Este índice nos permite definir el “grado de generalidad” de cada eje factorial. Decimos que un eje factorial representa un alto grado de generalidad cuando la inercia proyectada a lo largo del mismo resulta de la contribución de una gran cantidad de elementos (individuos o modalidades). Si un eje factorial esta asociado por un gran numero de modalidades, es decir si presenta un alto grado de generalidad, el eje resume una información muy rica. Al contrario, un eje factorial que presenta un grado de generalidad muy bajo aporta una información demasiado especifica (se trata de un eje hecho, por una sola modalidad). Elaboración y diseño en formato PDF, por la Oficina General del Sistema de Bibliotecas y Biblioteca Central UNMSM