3.1. Introducción a) Objetivo : b) Resumen gráfico : c) Componente
Anuncio

3. ALGUNOS MÉTODOS DE CLASIFICACIÓN
JERÁRQUICA ASCENDENTE
3.1. Introducción
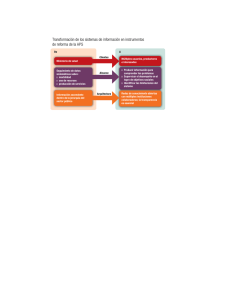
a) Objetivo :
Los métodos de clasificación jerárquica están destinados
a producir una representación gráfica de la información
contenida en la tabla de datos.
Los métodos de clasificación jerárquica representan de
manera sintética el resultado de las comparaciones entre
los objetos de una tabla T(n, p) observada, considerando
en esas comparaciones las p variables.
Una clasificación jerárquica (ascendente o descendente)
es una serie de particiones encajadas.
b) Resumen gráfico :
La representación gráfica del resultado de las comparaciones
entre los individuos observados está dada por :
- «árbol de clasificación» o «dendrograma».
c) Componente analógica del resultado de
una clasificación jerárquica ascendente :
- «índice de nivel de agregación».
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°14
d) Ejemplo: resultados de una clasificación
jerárquica ascendente
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°15
e) Definiciones : A partir del ejemplo precedente
La familia H de partes del conjunto I de seis objetos, construida por ese algoritmo de clasificación es la siguiente:
i la clase asociada al Obj.i, " i = 1, K ,6 .
Llamamos :{}
{1}; {2}; {3}; {4}; {5}; {6}; {1,2}; {3,4}; {3,4,5};
{1,2,3,4,5}; {1,2,3,4,5,6}
✔ La familia H contiene :
F El conjunto {1,2,3,4,5,6} que contiene todos los objetos del conjunto I.
F
Todos los conjuntos de cardinal 1, correspondientes
F
Los otros conjuntos de H son todos desjuntados, o
bien están inclusos unos en otros.
a cada objeto del conjunto I. Si i Î I Þ {}
i ÎH.
Si {}
i e {i'}Î H Þ {}
i Ç {i'} = f
o bien,
{}
i Ì {i'}, es decir que : {}
i Ç {i'} = {}
i .
✔ La familia H de partes del conjunto I construida con un
algoritmo ascendente forma una jerarquía ascendente.
✔ Una jerarquía ascendente produce una cadena de n
particiones encajadas compuestas de n a 1 clases.
✔ Los objetos a clasificar son los elementos terminales
de la jerarquía.
✔ Las clases encajadas de la jerarquía son los nudos del
árbol de clasificación.
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°16
✔ La jerarquía se llama «indiciada» si :
"{}
i Î H , existe un valor v(i ) ³ 0 ,
tal que si {}
i Ì {i'} Þ v(i ) £ v(i').
✔ El índice de agregación de una clase queda definido por
la «distancia» que determina el agrupamiento de los
objetos en la clase.
✔ El índice de agregación puede también ser normado. En
ese caso, cuando todos los elementos se encuentran ligados
entre ellos, a ese nudo del dendrograma le corresponde el
índice de valor 1.
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°17
f) Verificación : el índice utilizado en el ejemplo
anterior satisface las
propiedades de una distancia
ultramétrica.
1. La distancia entre dos objetos es siempre positiva o nula.
d({x},{y}) ³ 0 "x ; "y
ejemplos :
d({2},{5}) = 0.8
d({3},{6}) = 1
2. La distancia entre dos objetos idénticos es nula.
d({x},{x}) = 0 "x
ejemplo :
d({4},{4}) = 0
3. La distancia entre dos objetos es simétrica.
d({x},{y}) = d({y},{x}) "x ; "y
ejemplo :
d({1},{3}) = d ({3},{1}) = 0.8
4. La distancia evaluada entre dos objetos respeta
la desigualdad triangular.
d({x},{z}) £ d({x},{y}) + d({y},{z}) "x ; "y ; "z
ejemplo :
d ({1},{5}) < d ({1},{3}) + d ({3},{5})
0.8 < 0.8 + 0.6 = 1.4
5. La distancia evaluada entre dos objetos respeta la
desigualdad ultramétrica.
d({x},{z}) £ max d({x},{y}); d({y},{z}) "x, y , z
(
ejemplo :
)
d({1},{6}) £ max(d({1},{3}); d ({3},{6}) )
1 £ max( 0.8 ; 1 )
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°18
g) Equivalencia entre ultramétricas y
jerarquías indiciadas
A toda jerarquía indiciada le corresponde
una distancia ultramétrica d
Siendo:
*
H : una jerarquía de clases desjuntadas, o bien ligadas
por una relación de inclusión.
*
h : la clase más pequeña de H, tal que
{x} Ì h, {z} Ì h Þ h : {x, z}.
* d(x, z ) :
*
h’ :
el índice de agregación de la clase h.
la clase más pequeña de H, tal que
{y} Ì h' , {z} Ì h' Þ h': {y , z}.
* d(y , z ) :
el índice de agregación de la clase h’.
Como h Ç h' = {z}, se verifica que h Ì h' , o bien que
h' Ì h . De modo que : d (x, y ) £ d (x, z ), o bien
d (x, y ) £ d(y , z ).
Entonces d verifica la desigualdad ultramétrica:
d(x, y ) £ Max(d(x, z ), d(y , z ))
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°19
Sea :
A toda ultramétrica le corresponde una
jerarquía indiciada cuyo índice de
agregación es d.
h Î H ; h : {x, y}.
{z}Î H , un elemento aún no agregado.
Para agregar {z} en h es necesario calcular la distancia
ultramétrica de d(z , h ).
Pero d (z , x ) ³ d (x , y ) y d (z , y ) ³ d (x, y ). Caso contrario, los
elementos {z} y {x} o bien {z} e {y} hubieran sido agregados en
h antes que {x}e {y}.
Siendo d una ultramétrica :
d (z , x ) £ Max (d(x, y ), d(y , z ))
Þ d(z , x ) £ d (y , z )
d (z , y ) £ Max (d(x, y ), d(x, z ))
Þ d (z , y ) £ d (x , z )
de modo que : d (z , y ) = d(z , x )
Para una ultramétrica, todos los triángulos son isósceles,
con el lado más pequeño en la base.
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°20
h) ¿Qué significa clasificar un grupo de objetos ...?
Se trata de construir un «dendrograma» para un conjunto
de objetos sobre los cuales podemos evaluar el grado de similitud
por medio de una distancia.
i) ¿Cómo «transformar» la distancia empleada
en una distancia ultramétrica?
Si podemos transformar una distancia en una distancia
ultramétrica, modificando lo menos posible la distancia original
entre los objetos, entonces es posible construir un árbol de
clasificación indiciado.
j) La «transformación» se hace utilizando los
algoritmos de agregación de clases de objetos
Existen diferentes algoritmos (procesos iterativos) de
agregación que son utilizados corrientemente, por ejemplo :
✔ El método del vecino más cercano.
✔ El método de los centroides o de la distancia media.
✔ El método basado en el crecimiento mínimo del momento
de orden dos de las clases de particiones encajadas.
¿cómo proceden esos algoritmos y cuáles son sus
principales propiedades...?
Programa PRESTA - 1999 - Eduardo CRIVISQUI
Tr. N°21