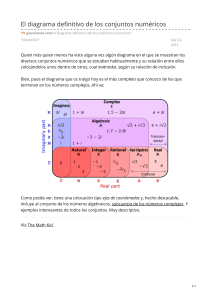
2- PRACTICO RELACIONES
Anuncio

Llamaremos par ordenado a una lista de dos objetos (a; b) donde a es un elemento de un
conjunto A y b es un elemento de un conjunto B .
(a1; b1) = (a2; b2) ↔ a1 = a2 y b1 = b2:
Dados dos conjuntos A y B se define el producto cartesiano A × B como el conjunto de todos los pares
ordenados.
A × B = {(a; b) ⁄ a ∈ A, b ∈ B}
Llamaremos RELACIÓN de A en B a un subconjunto del producto cartesiano, R ⊆ A × B.
Si (a; b) ∈ R se dicen que a y b están relacionados y se representa a R b en caso contrario se representa
a R/ b.
Propiedades de las relaciones:
Dados a, b y c ∈A y la relación R sobre A diremos que:
R es REFLEXIVA si ∀ a, aRa.
R es SIMÉTRICA si aRb→bRa
R es TRANSITIVA si ∀a, b, c; aRb y bRc →aRc.
EJERCICIOS
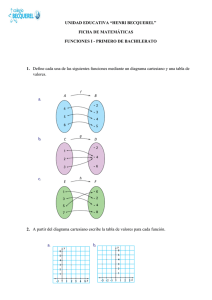
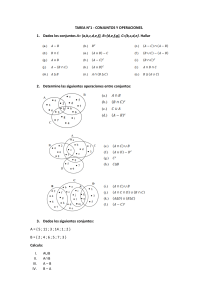
1.- Dados los conjuntos A= {a, b, c, d}; B= {1, 2, 3}; C= {a, c, 2, 3}
R1 = {(a, 2), (a, 1), (b, 3)};
R2 = {(a, 1), (c, 1)};
R3 = {(2, a), (3, c), (2, c)};
R4 = {(x, y) / x = y, x∈N, 0 < x ≤ 3}
a) Investigue si las siguientes son relaciones en los conjuntos que se indican:
R1: A→B ;
R1: A→C ;
R3: B→C ;
R2: A→B ;
R3: C→B ;
R2: A→C ;
R4: B→B ;
R3: A→B ;
R3: B→A ;
R4: B→C ;
b) Represente mediante diagrama las relaciones de la parte a).
2.- Dado el conjunto A= {a, b, c, d, e}, define tres relaciones diferentes en A y represente cada una de
ellas mediante: diagrama de flechas, diagrama cartesiano y en forma tabular.
Página 1
3.- Sea: A={a, b, c}, los siguientes diagramas representan relaciones de A×A.
Construye las tablas correspondientes de cada gráfico.
4.-Se consideran los siguientes conjuntos A= {x∈N / x(x+1) = 0}; B= {0, 1, 2} C= {3, 4, 5}
a) Halle A×B, C×A y B×C.
b) Determine las siguientes relaciones por extensión:
R1: A→B / R1= {(x, y) / x = y}
R2: C→A / R2= {(x, y) / x > 3y}
R3: B→C / R3= {(x, y) / x + y= 2}
5.- a) Nombre por extensión los siguientes conjuntos:
P = {x∈R/ x2-10x = -9};
Q = {x∈N / x es impar y o <x < 15};
S = {x∈Z / -2 ≤ x < 2 }
b) Sea A= Q ∩ P, B= S-P. Escribe A×B
6.- Dado: A= {1, 2, 3, 4, 5}
a) determine A×A
b) determine R={(x, y)∈ A×A / x es múltiplo de y}
c) escribe el D(R), Imag(R) y R-1.
d) ¿R es una relación de equivalencia?
7.- Dado A = {1, 2, 3, 4}, se consideran las siguientes relaciones definidas en A :
R1 ={(1, 1), (1, 2), (1, 3), (2, 2), (2, 1), (2, 3), (3, 3), (3, 1), (3, 2), (4, 4)}
R2={(1, 1), (1, 3), (2, 3), (3, 3), (3, 1), (3, 2), (4, 4) }
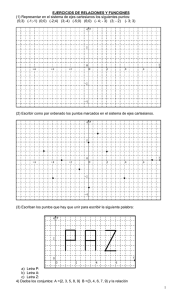
a) Represente cada una en un sistema de ejes cartesianos.
b) Indique en cada caso si la relación representada corresponde o no a una relación de equivalencia.
Justifique.
Página 2