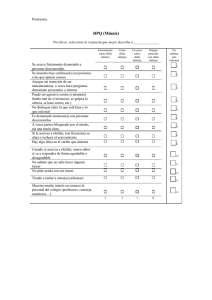
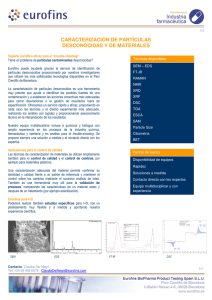
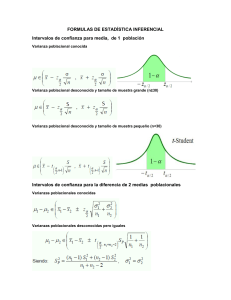
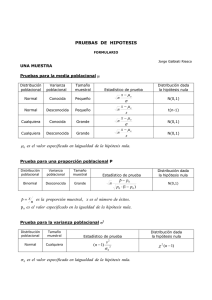
n s tx n s tx + ≤ ≤ −

Intervalos de confianza para la media o diferencia entre dos medias poblacionales, al nivel 1- . GH
confiabilidad
Poblaciones infinitas o muy grandes
Número de Suposición
Suposición sobre
poblaciones
sobre
desviación estándar
parámetro
muestra
Una población Grande
(n> 30) ó
pequeña
normal
Una población Pequeña
(n ” normal
1 FRQRFLGD
Dos
poblaciones
x - y
Dos
poblaciones
x - y
Una población
p
(proporción)
Grandes
(nx y ny> 30) ó
pequeñas
normal
Pequeñas
(nx ó ny ”
normal
1 GHVFRQRFLGD
n
Grande (n>
30, np>5 y
nq>5)
∑ (x
i
− x)
2
i =1
n −1
x −t
σ
n
s
n
α
( n −1),
2
1x 1y conocidas
≤ µ ≤ x + zα
2
≤ µ ≤
x +t
σ
n
( n−1),
2
α
2
s
n
2
σ x2 σ y
+
nx n y
2
σ x2 σ y
+
≤ µ x − µ y ≤ ( x − y) + zα
nx n y
2
( x − y) − zα
1x 1y desconocidas
sp =
Pequeñas
(nx ó ny ”
normal
x − zα
2
s=
Dos
poblaciones
x - y
Intervalo de confianza
(nx − 1) s x2 + (n y − 1) s 2y
nx + n y − 2
( x − y) − t
α
( nx + n y −2 ),
2
sp
1 1
1 1
+
≤ µ x − µ y ≤( x − y ) − t
+
α sp
( n x + n y −2 ),
nx n y
nx n y
2
df = nx + ny -2
1x  1y desconocidas
2
 s x2 s 2y 
 + 
 nx n y 

df = 
2
2
 s 2y 
 ss2 
 
 
 
n
 x  +  ny 
nx − 1 n y − 1
( x − y) − t
Número de éxitos
Número de repeticiones
α
2
s x − y ≤ µ x − µ y ≤( x − y ) + t
sx − y =
Estimador de p es f:
f=
df ,
f − zα
2
f (1 − f )
n
df ,
α
2
sx−y
2
s x2 s y
+
nx n y
≤ p ≤
f + zα
2
f (1 − f )
n