7.3 Árboles
Anuncio

Matemáticas Discretas
Tc1003
Teoría de Grafos
7.3 Árboles
•
•
Definición. Sea A un grafo. A recibe el nombre de árbol sí y sólo si:
A es conexo.
A no contiene circuitos.
Ejemplos:
Definición. Sea A un árbol. Un vértice de grado 1 se llama una hoja. Un vértice de
grado mayor que 1 se llama rama.
De las definiciones anteriores se desprenden las siguientes propiedades:
• Existe una trayectoria única entre dos vértices cualesquiera de un
árbol.
• El número de vértices es mayor en 1 al número de aristas.
• Un árbol con dos o más vértices tiene al menos dos hojas.
Ejemplo
Un grupo de ajedrecistas que luchan por un campeonato. Cada
ajedrecista tiene una única oportunidad para enfrentar al campeón vigente, y que el
perdedor de cualquier encuentro será eliminado de la contienda.
• Sea A = (V, E) un grafo no dirigido donde los vértices de V representan los
ajedrecistas y las aristas de E representan los encuentros.
• Sea V = { v1, v2, v3, v4, v5, v6, v7, v8, v9 }
Al inicio, v1 es el campeón vigente y que se dan los siguientes encuentros:
- v1 venció a v2, v3 y v4 y pierde con v5.
- v5 venció a v6 y v7 y pierde con v8.
- v8 pierde con v9.
El árbol que detalla esta situación, es el siguiente:
Los vértices v2, v3, v4, v6, v7, v9 son hojas.
Los vértices v1, v5, v8 son ramas.
Ngj/v2008
7.3 Árboles
230
Matemáticas Discretas
Tc1003
Teoría de Grafos
Definición. Sea G un grafo dirigido. Se dice que G es un árbol dirigido si se
convierte en un árbol cuando se ignoran las direcciones de sus aristas.
Definición. Un árbol con raíz es un árbol dirigido que posee exactamente un
vértice cuyo grado de entrada es 0 y los grados de entrada de todos los demás
vértices es 1.
El vértice con grado de entrada 0 se llama raíz de árbol. Un vértice cuyo
grado de salida es 0 se llama hoja. Un vértice cuyo grado de salida es diferente de 0
se llama rama.
Definición. Sea vi una rama de un árbol con raíz. Se dice que Vk es un hijo de Vi si
existe una arista dirigida de Vi a Vk , además se dice que vi es padre de Vk .
En un árbol con raíz se dice que los vértices son hermanos si son hijos del
mismo vértice.
Ejemplo
Un hombre que tiene dos hijos, de los cuales uno no tiene hijos y el otro tiene tres
hijos.
Solución
Ngj/v2008
7.3 Árboles
231
Matemáticas Discretas
Tc1003
Teoría de Grafos
Definición. Sea A un árbol con raíz. Se dice que A es un árbol binario si cada rama
tiene exactamente dos hijos.
Ejemplo
•
•
•
•
•
•
El árbol anterior muestra el número de encuentros en un torneo de
eliminación simple con 8 competidores.
Se juegan un total 7 encuentros a saber:
Cuatro encuentros en la primera ronda.
Dos encuentros en la segunda ronda.
El encuentro final.
En total son 7 encuentros.
En este árbol binario, las hojas representan a los competidores en el torneo y las
ramas a los ganadores de los encuentros o, equivalentemente los encuentros
jugados en el torneo.
Si se llama r el número de ramas y h el número de hojas en un árbol binario, se
puede demostrar que:
r = h –1.
Ngj/v2008
7.3 Árboles
232
Matemáticas Discretas
Tc1003
Teoría de Grafos
Si un grafo tiene un vértice U o que solo contiene una diferente de U o − U 1 (a sí
mismo) entonces es un árbol
árbol
no es árbol
este vértice tiene dos
trayectorias
En general
Altura = 3 (el nivel mas grande)
raíz = que no tiene padre (inicial)
padre = que tiene hijo(s)
hoja = no tiene hijo(s), tiene padre
Conjunto de árboles = Bosque.
Árbol ordenado: tiene nivel, los hijos de izquierda a derecha.
n-árbol: cuando cada padre tiene a lo más n hijos
árbol binario: cada padre tiene a lo más 2 hijos.
Ngj/v2008
7.3 Árboles
233
Matemáticas Discretas
Tc1003
Teoría de Grafos
Para:
sub - árboles
¿Cuántos subárboles?
Altura = ?
6
5
V0 − V1
Ngj/v2008
V 0 − V3
V1
V0 − V 2
V 2
V4
V6
V8
V13
7.3 Árboles
V3
234
Matemáticas Discretas
Tc1003
Teoría de Grafos
Notación polaca
La evaluación se realiza de derecha a izquierda y de abajo hacia arriba
Ejemplo:
[3 ∗ (1 − x ) ÷ (4 + (7 − ( y + 2)))]∗ [7 + ( y ÷ x )]
Primero: paréntesis interiores
Árbol etiquetado
EJEMPLO:
5
2
6
1
7
3
9
4
8
8= ?
5, 6, 7, 9, 8
4= ?
5, 2, 3, 4
(3 − (2 ∗ x )) + ((x − 2) − (3 + x ))
((2 ∗ x ) − 3) + ((x − 2) − (3 + x ))
Ngj/v2008
7.3 Árboles
235
Matemáticas Discretas
Tc1003
Teoría de Grafos
Árboles de expansión
Un árbol T es un árbol de expansión de un grafo G si T es un subgrafo de G que
contiene todos los vértices de G. [Johnsonbaugh, 392]
Ejemplos:
Grafo:
Árbol de expansión:
Árboles enraizados
En ciencias computacionales los árboles tienen muchas veces vértices principales
que pueden utilizarse para dar a los árboles estructuras dirigidas. En general, se
puede transformar cualquier grafo no dirigido en un grafo dirigido poniéndole
flechas. Si el grafo es un árbol lo que se obtiene es un árbol dirigido. Si todas las
flechas parten de un solo vértice se llama árbol enraizado. [Ross, 451]
Ngj/v2008
7.3 Árboles
236
Matemáticas Discretas
Tc1003
Teoría de Grafos
Actividades colaborativas
Hoja de trabajo
1. Para las siguientes expresiones, construye un árbol con notación polaca.
a) (4 + (7 − ( y + 2))) ∗ (7 + ( y ÷ x ))
b) ((1 − x ) ∗ 3) ÷ ((( y − 2 ) − 7 ) + 4) ∗ (( y ÷ x ) + 7 )
2. Para la siguiente secuencia de números, construye un árbol acomodando los
mayores de lado izquierdo del nodo y los menores de lado derecho del nodo
a. 10, 14, 2, 4, 13, 1, 7, 8, 11, 16, 5, 20
b. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
3. La siguiente matriz muestra una tabla de direcciones (registros) en donde se
encuentra almacenada cierta información. La columna “derecha” contiene el
número de registro de la información antecesora (nodo hijo derecho). La columna
“izquierda” contiene el número de registro de la información sucesora (nodo hijo
izquierdo). Por medio de un árbol binario, representa la tabla de direcciones. El
nodo raíz es el registro número 5.
Número de 1
registro
derecha
información a
izquierda
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
b
13
c
d
2
e
6
f
8
g
7
h
14
i
j
k
12
3
l
4
11
m
n
p
4. El siguiente es el programa analítico del curso de Matemáticas Discretas,
representa en forma de árbol este contenido.
1 Conceptos fundamentales
1.1 Breve historia de las matemáticas
1.1.1 Civilizaciones, historia y matemáticos
1.1.2 Clasificación de las matemáticas
1.2 Aritmética
1.2.1 Introducción
1.2.2 Los números
1.2.3 Definición de los números
1.2.4 Operaciones de los números
• Adición y Sustracción
• Multiplicación y División
• Operación binaria
1.2.5 Propiedades de los números
• Cerradura, inverso y neutro
• Conmutativa y Asociativa
• Distributiva
1.2.6 Propiedades de las operaciones de los números
• Para los números enteros
• Para los números racionales
Ngj/v2008
7.3 Árboles
237
Matemáticas Discretas
Tc1003
Teoría de Grafos
2 Lógica Matemática
2.1 Lógica proposicional
2.1.1 Sintaxis de lógica proposicional
2.1.2 Semántica de lógica proposicional
2.2 Lógica de predicados de primer orden
2.2.1 Sintaxis y lógica de predicados de primer orden
2.2.2 Proposiciones con cuantificadores
2.3 Métodos de demostración
2.3.1 Método del absurdo
2.3.2 Resolución
2.3.3 Deducción natural
3 Los conjuntos
3.1 Definición
3.2 Numerabilidad de conjuntos
3.3 Tipos de conjuntos numéricos
3.4 Operaciones con conjuntos
3.5 Propiedades de los conjuntos
4 Relaciones y funciones
4.1 Relaciones
4.1.1 Definición de relación
4.1.2 Propiedades de las relaciones
4.1.3 Tipos de relaciones
4.2 Funciones
4.2.1 Definición
4.2.2 Tipos de funciones
4.2.3 Operaciones
4.2.4 Iteración y recursividad
5 Estructuras Algebraicas
5.1 Matrices
5.1.1 Definición
5.1.2 Tipos de matrices
5.1.2 Operaciones con matrices
5.2 Estructuras Algebraicas
5.2.1 Introducción
5.2.2 Matemática abstracta
5.2.2.1 Definición
5.2.2.2 Estructuras algebraicas
5.3 Álgebra Booleana
5.3.1 Conceptos
5.3.2 Operaciones booleanas
5.3.3 Leyes
5.3.4 Forma Normal Disyuntiva y Forma Normal Conjuntiva
6 Análisis combinatorio
6.1 Principio de conteo
6.2 Permutaciones
6.3 Combinaciones
6.4 Cuatro conceptos
7 Teoría de grafos
7.1 Definiciones
7.2 Trayectorias y circuitos de Euler
7.3 Trayectorias y circuitos de Hamilton
7.4 Árboles
Ngj/v2008
7.3 Árboles
238
Matemáticas Discretas
Tc1003
Teoría de Grafos
3. La final masculina de Wimbledon es ganada por el primer jugador que gane tres
de cinco sets en un juego. Si C y M detonan a los jugadores, dibuja un diagrama de
árbol que demuestre todas las formas posibles en que se puede decidir el juego.
4. Un rumor se difunde como sigue. El que lo origina llama a dos personas por
teléfono, Cada una de estas personas telefonea a tres amigos, cada uno de los cuales
a su vez llama a otros 5 más. Nadie recibe más de una llamada y nadie llama al que
lo origino. Por medio de un diagrama de árbol, representa como se difunde un
rumor.
Ngj/v2008
7.3 Árboles
239
Matemáticas Discretas
Tc1003
Teoría de Grafos
Actividades de Árboles
Solución
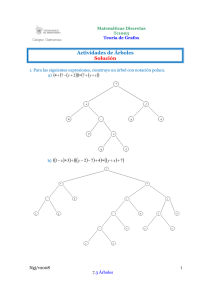
1. Para las siguientes expresiones, construye un árbol con notación polaca.
a) (4 + (7 − ( y + 2))) ∗ (7 + ( y ÷ x ))
b) ((1 − x ) ∗ 3) ÷ ((( y − 2) − 7 ) + 4 ) ∗ (( y ÷ x ) + 7 )
Ngj/v2008
7.3 Árboles
240
Matemáticas Discretas
Tc1003
Teoría de Grafos
2. Para la siguiente secuencia de números, construye un árbol acomodando los
mayores de lado izquierdo del nodo y los menores de lado derecho del nodo
a) 10, 14, 2, 4, 13, 1, 7, 8, 11, 16, 5, 20
b) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Ngj/v2008
7.3 Árboles
241
Matemáticas Discretas
Tc1003
Teoría de Grafos
3. La siguiente matriz muestra una tabla de direcciones (registros) en donde se
encuentra almacenada cierta información. La columna “derecha” contiene el
número de registro de la información antecesora (nodo hijo derecho). La columna
“izquierda” contiene el número de registro de la información sucesora (nodo hijo
izquierdo). Por medio de un árbol binario, representa la tabla de direcciones. El
nodo raíz es el registro número 5.
Número de 1
registro
derecha
información a
izquierda
Ngj/v2008
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
b
13
c
d
2
e
6
f
8
g
7
h
14
i
j
k
12
3
l
4
11
m
n
p
7.3 Árboles
242
Matemáticas Discretas
Tc1003
Teoría de Grafos
4. El siguiente es el programa analítico del curso de Matemáticas Discretas,
representa en forma de árbol este contenido.
3. La final masculina de Wimbledon es ganada por el primer jugador que gane tres
de cinco sets en un juego. Si C y M detonan a los jugadores, dibuja un diagrama de
árbol que demuestre todas las formas posibles en que se puede decidir el juego.
Ngj/v2008
7.3 Árboles
243
Matemáticas Discretas
Tc1003
Teoría de Grafos
4. Un rumor se difunde como sigue. El que lo origina llama a dos personas por
teléfono, Cada una de estas personas telefonea a tres amigos, cada uno de los cuales
a su vez llama a otros 5 más. Nadie recibe más de una llamada y nadie llama al que
lo origino. Por medio de un diagrama de árbol, representa como se difunde un
rumor.
Ngj/v2008
7.3 Árboles
244