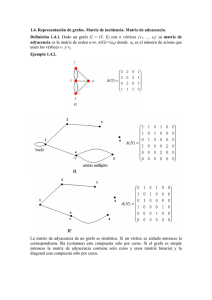
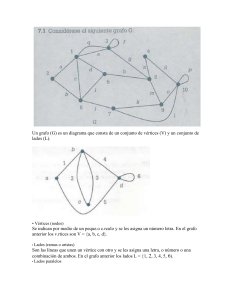
GRAFOS. SOLUCIONES 1. Los vértices A, Z y O pueden estar
Anuncio

GRAFOS. SOLUCIONES D 1. A O Z C Los vértices A, Z y O pueden estar colocados de otra forma, ya que no nos dicen que 2 torres se ven desde C. Pintando D de un color 1, necesitamos pintar A, Z y O de otro color, además los colores de A y Z (O y Z) deben ser distintos, pero podemos pintar Ay O de un mismo color 2 y así Z de color 3, por último podemos pintar C de color 1 o 3, es decir hacen falta 3 colores. Consumata puede ver sólo 1 banderas de colores distintos. La matriz de adyacencia del grafo dibujado es A 0 1 1 0 1 C 1 0 0 1 0 D 1 0 0 1 1 O 0 1 1 0 1 Z 1 0 1 1 0 2. Los grafos primero, tercero y quinto son isomorfos. Los grafos segundo y cuarto también. 3. Ba Bo NY Mi Ma El grado de cada vértice representa el número de vuelos que tienen como salida o destino el aeropuerto correspondiente. 5. Contando los grados de los vértices vemos que hay exactamente 2 de grado impar, así que es posible hacer el recorrido (pero no comenzando y acabando en el mismo vértice). 6. Supongamos que como mucho hay 1 vértice de grado 1, por el teorema fundamental tendríamos entonces que 2n-2=2|V|≥2(n-1)+1=2n-1 (Contradicción) 7. a) NO, es contraible a K5 b) NO, es contraible a K5 c) SI d) NO, es isomorfo a K3,3 9. Un grafo simple debe tener como matriz de adyacencia una matriz simétrica cuyos elementos sean sólo 0’s y 1’s y con elementos nulos en la diagonal principal. Un grafo completo debe tener como matriz de adyacencia una matriz simétrica con 0’s en la diagonal y 1’s en el resto. 10. Para el primer grafo tenemos 0 1 0 0 1 1 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 0 0 0 1 0 1 1 0 0 para el segundo grafo tenemos la misma matriz. 12.a) Tenemos 2|V|≤4·25=100, así el número máximo de aristas será 50. n 12.b) Tenemos ≥ 52 , de donde n≥11 2 13. Representando cada habitación (incluso el exterior) como un vértice y cada puerta como una arista entre los vértices (habitaciones) correspondientes tenemos el grafo Que se observa tiene más de 2 vértices de grado impar, así que no podemos realizar el recorrido.