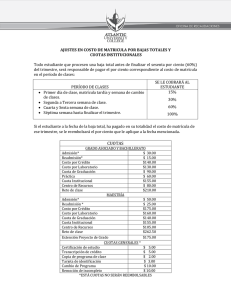
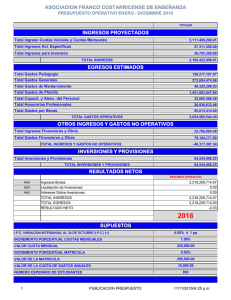
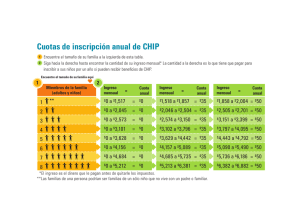
Escuela de Estudios Industriales y Empresariales 2. Una

 Escuela de Estudios Industriales y Empresariales MATEMÁTICAS FINANCIERAS Ing. Edwin Alberto Garavito Hernández TALLER
(Relaciones de equivalencia entre tasas)
1.
Transferir las siguientes tasas:
a. 12% Efectivo anual Æ Nominal anual mes vencido
b. 24% nominal anual trimestre vencido Æ Efectivo Anual.
c. 20% nominal anual trimestre anticipado Æ Nominal anual mes vencido
d. 15% nominal semestral mes anticipado Æ nominal anual semestre anticipado
e. 1.1% nominal mensual quincenal anticipado Æ Efectivo anual anticipado
2. Una entidad financiera me ofrece un crédito por $5.000.000 por seis meses con una tasa nominal
anual del 8% mes anticipado. ¿cuánto tendré que regresar al finalizar los seis meses?
(ANUALIDADES)
3.
Se solicita un préstamo por valor de $10 millones en una entidad que le ofrece el 12% nominal anual
trimestre anticipado, para pagar en cuotas mensuales vencidas durante tres años. ¿Cuál es el valor
de las cuotas?
4.
Cuando Armando cumplió 6 años de edad, su abuelo le obsequió $10’000.000 para que fueran invertidos y,
posteriormente, utilizados en su educación universitaria. Sus padres depositaron el dinero en una cuenta que
paga el 14.4% nominal anual con capitalización quincenal. Si la tasa de interés permanece constante, e inicia
sus estudios al cumplir los 18 años, ¿cuánto podrá pagar semestralmente durante 5 años de
matrícula, si decide retirar la misma cantidad al inicio de cada uno de los semestres?
5.
Un crédito por valor de 100 millones de pesos en una entidad financiera se obtiene con las siguientes
condiciones: Plazo cuatro años, Pagos mensuales iguales vencidos por valor “X” durante los dos primeros años
que se incrementan un 10% para los dos últimos años. Pagos semestrales iguales vencidos por valor
equivalente a 2X por los cuatro años. Un pago adicional por valor de 10 millones al finalizar el segundo año de
cuotas. Calcular el valor de X si el interés cobrado por la entidad es del 15% nominal anual trimestre anticipado.
6.
Necesita retirar dentro de cuatro años una cantidad X, para lo cual comienza ahorrando cada mes
una cantidad A durante los dos primeros años, la cual incrementa para los dos siguientes un 20%. La
entidad donde guarda su dinero le reconoce un interés del 6% nominal anual semestre anticipado.
Una vez usted consigna la cuota correspondiente al mes 22 revisa el saldo y le aparecen ahorrados
$4’250.000.
a. Realice el análisis a partir del diagrama de flujo de caja
b. Plantee las ecuaciones que le permitan llegar al valor de las cuotas y de la cantidad a retirar
X, usando la representación simplificada de los factores
c. Calcule el valor de las cuotas y de X
(SERIES ARITMÉTICAS)
7. Hoy inicia con un ahorro de $X, y cada mes incrementa esa cantidad en $50.000. Si desea retirar el
dinero dentro de 42 meses, y la entidad donde deposita ese dinero le ofrece una tasa del 9% nominal
anual trimestre anticipado, ¿Qué cantidad retira?
8. Un préstamo de $30’000.000 al 15% efectivo anual, es pactado a pagos mensuales iguales vencidos
por 2 años. Sin embargo, por problemas financieros, luego de pagar la cuota número 10, el deudor
acude a la entidad que le hizo el préstamo para solicitar que le ayuden a mejorar su situación, para lo
cual solicita una re liquidación del saldo de la deuda con nuevo plazo de 24 meses para el saldo y un
préstamo adicional de 5 millones de pesos. Además que se le permita no hacer pago alguno durante
ocho meses (período de gracia ocho meses para la nueva deuda). La entidad le acepta las
condiciones, englobando el saldo de la deuda y el nuevo monto de 5 millones en un solo crédito con
Ing. Edwin Alberto Garavito Hernández
INGENIERÍA ECONÓMICA, ………….3/3
una tasa del 18% efectivo anual, y pactando cuotas trimestrales vencidas por los dos años con
incrementos de $100.000 cada trimestre.
•
•
¿Cuál es el valor de cada una de las primeras 10 cuotas mensuales?
¿Cuál es el valor de la primera cuota del nuevo crédito?
(SERIES GEOMÉTRICAS)
9.
Calcular el valor de la primer cuota y de la cuota 20 de un crédito de $ 30 millones con una tasa de
1.2% mensual vencido pagaderos en cuotas mensuales vencidas con incrementos del 0.5% cada
mes durante 3 años.
10. Se establece un plan de ahorro programado con una cuota mensual que inicia con “$M” y se va
incrementando en un 2% cada mes, durante 5 años y un ahorro extraordinario semestral que inicia
con “$S” y se incrementa cada semestre en un 5% durante tres años. Al finalizar el año 5 retira un
total de Y millones de pesos.
a. Cuál será el valor de Y en función de M y S?
b. Si el valor retirado es de $20 millones, y M equivale a la mitad de S, ¿Cuál será el valor de la
cuota que cancelará en el mes 24?
(ANUALIDADES CON CRECIMIENTO GEOMÉTRICO)
11. Calcule el valor de las cuotas del primer año y del último año de pagos de un crédito de $20 millones
el cual se ha pactado a 5 años con cuotas mensuales iguales con crecimiento cada año del 5%. La
tasa de interés cobrada por la entidad financiera es del 18% nominal anual semestre vencido.
12. Un crédito por valor de $50 millones se pagará en cuatro años con cuotas iguales mensuales por
valor $A que se incrementan cada año en un 5%, y cuotas semestrales vencidas por valor $B que se
incrementan cada año en 2%. Luego de pagar la cuota 24, el saldo del crédito es de $35 millones.
Calcular el valor de A y de B si la tasa que cobra la entidad financiera es del 1.5% efectivo mensual
vencido.
13. Desea retirar 50 millones de pesos dentro de cinco años, y se dispone a ahorrar cada trimestre una
cantidad M incrementándola cada año en un 1%, igualmente, cada semestre ahorra una cantidad N
incrementándola cada dos años en un 5%. Luego de hacer la consignación correspondiente al
finalizar el tercer año el saldo que tiene en la cuenta es de $30 millones. La entidad financiera le
reconoce un interés del 0.5% efectivo mensual vencido. Calcular los valores M y N.
14. Se desea adquirir una vivienda sobre planos que será entregada en un año, por un valor de
$180’000.000. Es necesario pagar una cuota inicial correspondiente al 30% del valor total, pagando
5’000.000 para separarla y el resto de la cuota inicial diferido a 12 meses, tiempo que demora la
entrega. Al ser entregada la vivienda, se accede a un crédito en una entidad financiera que le ofrece
una tasa del 14% anual capitalizable cada trimestre anticipado, el cual se pagará en cuotas iguales
mensuales que crecerán cada año en un 5%; adicionalmente cuotas semestrales equivalentes a la
mitad de la mensual (también se incrementan en 5%). También se planea un pago extraordinario de
$10’000.000 en el mes 35 del crédito.
a. Elabore el diagrama de flujo de caja de todo el proyecto (incluyendo cuota inicial).
b. Calcular el valor de las cuotas que se pagarán a la entidad financiera.
15. Para poder realizar un viaje, se dispone a ahorrar por 5 años una cuota fija mensual por valor “Q” que
incrementa cada año un 3% en una entidad que le ofrece un interés del 6% nominal anual semestre
anticipado. También ahorra una cuota semestral “R” la cual incrementa un 5% cada año por cuatro
años y adicionalmente se compromete con un ahorro anual por valor “M” que incrementa en un 5%
cada año pero solo por tres años. En el mes 20 sabe que recibirá el dinero de un CDT que había
establecido por tres años y cuyo monto inicial era de “T” pesos, con una rentabilidad del 3% efectivo
semestral. Al recibir el dinero, lo depositará en el mismo plan de ahorro.
Ing. Edwin Alberto Garavito Hernández
INGENIERÍA ECONÓMICA, ………….3/3
a. Desarrollar el diagrama de flujo de efectivo correspondiente.
b. Calcule el valor que retirará al cabo de los 5 años en función de las variables establecidas
c. Se sabe que en el mes 28 luego de hacer los ahorros respectivos el saldo en la cuenta es
“S”. Plantee la ecuación correspondiente a la relación de este saldo con las variables
establecidas para los ahorros Q, R, M, T
EVALUACIÓN DE ALTERNATIVAS OPERACIONALES.
EVALUACIÓN DE ALTERNATIVAS CON VIDAS IGUALES VPN - VFN
1.
Se tienen tres tipos de máquinas cuyos costos se presentan en la tabla siguiente (en miles de pesos). Se
supone que los ingresos que generan las tres alternativas son iguales. La TMAR (tasa mínima atractiva de
rendimiento, i*)= 10% efectivo anual.
Costo inicial
Costo anual de operación
Valor de salvamento
VIDA ÚTIL (Años)
ENERGÍA
ELÉCTRICA
2.500
900
200
5
GAS
3.500
700
350
5
SOLAR
6.000
50
100
5
EVALUACIÓN DE ALTERNATIVAS CON VIDAS DIFERENTES
2.
Para la ejecución de un proyecto a seis años, se requiere arrendar una oficina en la ciudad, y se tienen dos
alternativas disponibles. Los costos de cada una se muestran a continuación (miles de pesos): (usar TMAR=
15%)
ALTERNATIVA A
ALTERNATIVA B
Costo inicial (adecuaciones)
15.000
18.000
Costo anual de arrendamiento
3.500
3100
Costo mensual de servicios
250
200
Término de Arrendamiento (años)
6
9
TASA INTERNA DE RETORNO.
3. Se desea saber si es atractivo invertir en un negocio para el cual es necesario hacer una inversión inicial para
compra de equipos y adecuaciones locativas por valor de $50 millones de pesos. Los costos de operación
mensual ascienden a 6 millones y se incrementan en un 5% cada año. Adicionalmente hay costo de
actualización de equipos que se genera cada seis meses de operación y equivale a $2. Millones y se incrementa
en 2% cada año. Los ingresos proyectados ascienden a $8 millones mensuales, con incrementos cada año de
5%, y el valor de reposición de los equipos, considerando una vida de 5 años es de $ 6 millones
4.
Se desea estimar la rentabilidad promedio que dejará un proyecto de inversión con las siguientes características
•
Vida útil 10 años
•
Inversión inicial: $50 millones
•
Costos operativos (mensuales): $30% de los ingresos
•
Gastos semestrales por mantenimiento: 2’500.000 crecen un 5% cada año
•
Gastos anuales de impuestos: 3 millones, crece un 3% cada año
•
Ingresos mensuales por ventas: $6.5 millones en promedio, pero su comportamiento es aleatorio siguiendo
una distribución normal con desviación de 0.8 millones