PROGRAMACIÓN LINEAL CONCEPTOS BÁSICOS DE
Anuncio
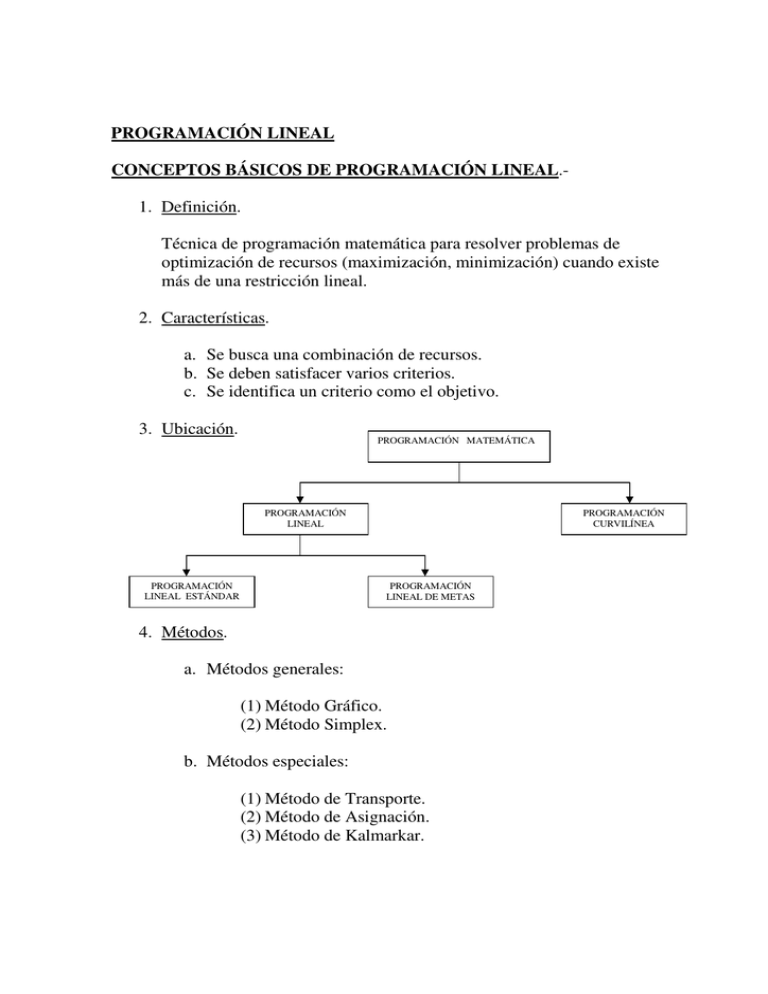
PROGRAMACIÓN LINEAL CONCEPTOS BÁSICOS DE PROGRAMACIÓN LINEAL.1. Definición. Técnica de programación matemática para resolver problemas de optimización de recursos (maximización, minimización) cuando existe más de una restricción lineal. 2. Características. a. Se busca una combinación de recursos. b. Se deben satisfacer varios criterios. c. Se identifica un criterio como el objetivo. 3. Ubicación. PROGRAMACIÓN MATEMÁTICA PROGRAMACIÓN LINEAL PROGRAMACIÓN LINEAL ESTÁNDAR PROGRAMACIÓN CURVILÍNEA PROGRAMACIÓN LINEAL DE METAS 4. Métodos. a. Métodos generales: (1) Método Gráfico. (2) Método Simplex. b. Métodos especiales: (1) Método de Transporte. (2) Método de Asignación. (3) Método de Kalmarkar. 5. Supuestos. a. Linealidad: (1) Todas las variables deben ser lineales (exponente = 1). (2) Todos los coeficientes deben ser constantes. (3) Todas las operaciones son sumas o restas. b. Determinismo: Debe conocerse con certeza el comportamiento de todas las variables y de todos los coeficientes. c. Objetivo único: Debe haber un solo objetivo. 6. Inconvenientes. a. Necesidad de computador electrónico. b. Costos de formulación del problema. METODO GRÁFICO DE PROGRAMACIÓN LINEAL.1. Concepto. Representación en un sistema de ejes coordenados de las zonas del plano definidas por las inecuaciones de restricción para determinar una figura que satisfaga todas y cada una de ellas. 2. Ventajas. a. Conocimiento de los conceptos básicos de la programación Lineal. b. Facilita la comprensión de los métodos más complejos. c. Desventajas. Sólo sirve para problemas con dos variables de decisión. d. Etapas. a. b. c. d. Formulación del problema. Trazado del gráfico. Obtención de la solución óptima. Análisis gráfico de sensibilidad. REPRESENTACIÓN DE VARIABLES. [A] Forma. Carácter que representa un determinado producto. [B] Modalidades. 1. Serie: Dos letras mayúsculas de imprenta (A y B o X e Y). 2. Subíndice: Una letra mayúscula de imprenta con subíndices (X) (1 y 2). 3. Nemotecnia: Dos letras mayúsculas de imprenta representativas. RESTRICCIONES. [A] Concepto de restricción. Conjunto de condiciones exigidas, relacionadas con los recursos involucrados en un problema, que debe satisfacer toda solución. [B] Tipos de restricciones. 1. Restricciones de capacidad: • Se deben a la cantidad disponible de: - Equipo - Espacio - Mano de obra • Ejemplo: Tiempo disponible en la máquina N° 1. 2. Restricciones de mercado: • Son límites de la cantidad de producto (bien o servicio) que puede venderse o usarse. • Puede ser: - Inferior - Superior - Ambos • Ejemplo: No pueden venderse más de 200 litros de gasolina. 3. Restricciones de disponibilidad: • Son límites ocasionados por la escasez de recursos. - Materias primas. - Fuerza de trabajo. - Financiamiento. - Otros. • Ejemplo: La cantidad de litros de combustible para mezcla es de 30.000 litros. 4. Restricciones de calidad: • Son restricciones que limitan la mezcla de ingredientes y que por lo tanto determinan la calidad de los productos resultantes. • Ejemplo: El octanaje que debe tener una mezcla de gasolina de aviación. 5. Restricciones de equilibrio: • Son restricciones de tecnología de producción o equilibrio de materiales. • Determinan la salida de un proceso como una función de las entradas, muchas veces con una pérdida por desperdicios. • Ejemplo: Entradas de troncos de pino y abeto usados para producir hojas de madera contrachapada. 6. Restricciones de definición: • Son restricciones que definen una variable. • Muchas veces provienen de definiciones contables. • Ejemplo: El inventario final de productos terminados debe ser igual a 0. ANÁLISIS DE SENSIBILIDAD A. Concepto de análisis de sensibilidad. Estudio del efecto de los cambios en los parámetros del problema, sobre la solución óptima de Programación Lineal. B. Importancia del análisis de sensibilidad. 1. Los modelos de Programación Lineal son con frecuencia grandes y costosos, debido a lo cual no es eficiente usarlos para un solo caso. 2. Los elementos que se dan como datos para un problema, muchas veces son aproximaciones, debido a lo cual es necesario examinar más de un conjunto de circunstancias. C. Tipos de análisis de sensibilidad. 1. Sensibilidad de la función objetivo: a. Cambios en los coeficientes Determinar la gama de optimalidad para la pendiente de los parámetros de la función objetivo que mantendrá inalterable la solución óptima de un modelo determinado. b. Cambios en el término independiente (LD) 2. Sensibilidad de las restricciones: a. Cambios en los coeficientes de las restricciones. b. Cambios en el término independiente de las restricciones. (LD) c. Adición de nuevas restricciones. 3. Sensibilidad de las limitaciones: a. Cambios en la limitación de las abscisas. b. Cambios en la limitación de las ordenadas. 4. Adición de nuevas variables MÉTODO GRÁFICO DE PROGRAMACIÓN LINEAL Modelo I. FORMULACIÓN DEL PROBLEMA.A. Objetivo. 1. Variables: 2. Enunciado: 3. Función: Z = B. Restricciones. 1. Restricción de ________________ : 2. Restricción de ________________ : n. Restricción de ________________ : C. Limitaciones. 1. Limitación de abscisas: 2. Limitación de ordenadas: II. TRAZADO DEL GRÁFICO.A. Determinación de extremos. 1. __________________ 2. __________________ 3. __________________ 4. __________________ B. Región Factible. En el gráfico C. Líneas de restricción. En el gráfico Gráfico: III. OBTENCIÓN DE LA SOLUCIÓN ÓPTIMA.A. Frontera extrema. En el gráfico B. Puntos de intersección. Punto 1 Punto 2 Punto n C. Coordenadas de los puntos de intersección. 1. Uso de los ejes: Punto ___ = ( Punto ___ = ( , , 2. Reemplazo de valores: Punto ___ = ( , Punto ___ = ( , ) ) ) ) 2. Resolución de ecuaciones simultáneas: Punto ___ = ( , ) Punto ___ = ( , ) D. Sustitución de la función objetivo. 1. Punto 1: 2. Punto 2: 3. Punto n: E. Determinación del valor óptimo. 1. El valor mayor/menor es $ ______/ 2. El punto es el óptimo es ______/. 3. La solución es producir: a. Unidades del producto ____ = _____/ b. Unidades del producto ____ = _____/ IV. ANÁLISIS DE SENSIBILIDAD A. Coeficientes de la función objetivo: 1. C1 = 2. C2 = B. Parámetros de las rectas involucradas: 1. 2. C. Declives de las líneas: 1. 2. ≤ ≤ C1 C2 C2 C1 ≤ /* C2 = = ≤ ≤ /* C1 = = ≤ D. Gama de optimalidad: Disminución N° Variable Coeficiente actual Permitido Mínimo 1 2 Aumento Permitido Máximo PROGRAMACIÓN LINEAL PROBLEMAS DEL MÉTODO GRÁFICO PROBLEMA N° 1 “PROBLEMA DE PRODUCCIÓN” Un fabricante está tratando de decidir sobre las cantidades de producción óptimas para dos artículos: mesas y sillas. Se cuenta con 96 unidades de material y con 72 horas de mano de obra. Cada mesa requiere 12 unidades de material y 6 horas de mano de obra. Por otra parte, las sillas usan 8 unidades de material cada una y necesitan 12 horas de mano de obra por silla. El margen de contribución es el mismo para las mesas que para las sillas: 5 unidades monetarias por unidad. El fabricante prometió construir por lo menos 2 mesas. PROBLEMA N° 2 “PROBLEMA DE DIETA” Un comprador está tratando de seleccionar la combinación más barata de dos alimentos, que debe cumplir con ciertas necesidades diarias de vitaminas. Los requerimientos vitamínicos son por lo menos 40 unidades de vitamina W, 50 unidades de vitamina X y 49 unidades de vitamina Y. Cada onza del alimento A proporciona 4 unidades de vitamina W, 10 unidades de vitamina X y 7 unidades de vitamina Y; cada onza del alimento B suministra 10 unidades de W, 5 unidades de X y 7 unidades de Y. El alimento A cuesta 5 monedas/onza y el alimento B vale 8 monedas/onza. PROBLEMA N° 3 “PROBLEMA DE FABRICACIÓN” Una compañía fabrica palos de jockey y juegos de ajedrez. Cada palo de hockey genera un beneficio de dos unidades monetarias y cada juego de ajedrez entrega una utilidad de cuatro unidades monetarias. Un palo de hockey requiere cuatro horas de procesamiento en el centro de mecanizado “A” y dos horas en el centro de mecanizado “B”. Un juego de ajedrez necesita seis horas en el centro “A”, seis en el “B” y una hora en el “C”. El centro de mecanizado “A” tiene una capacidad máxima diaria de 120 horas, el centro “B” posee 72 horas y el “C” 10 horas. Si la empresa desea optimizar el beneficio, ¿cuántos palos de hockey y cuántos juegos de ajedrez debe fabricar al día? PROBLEMA N° 4 “PROBLEMA DE MEZCLAS” Una empresa que da servicio de limpieza prepara sus propios compuestos mezclando dos ingredientes. Hace esto para obtener un compuesto que tiene lo que considera una combinación apropiada de fosfatos y cloruro. Un ingrediente tiene dos porciones de fosfato y cinco porciones de cloruro y cuesta 5.0 unidades monetarias el litro. El otro ingrediente tiene cinco porciones de fosfato y dos porciones de cloruro y vale 1.5 unidades monetarias el litro. La firma necesita que la mezcla final tenga más de diez porciones de fosfato y diez de cloruro. Determinar la mezcla que optimiza el costo total.