1.20 1.76 2 1.50 x xy zy yz xxz + + = + + = + = 0, 1, 0.75 xyz

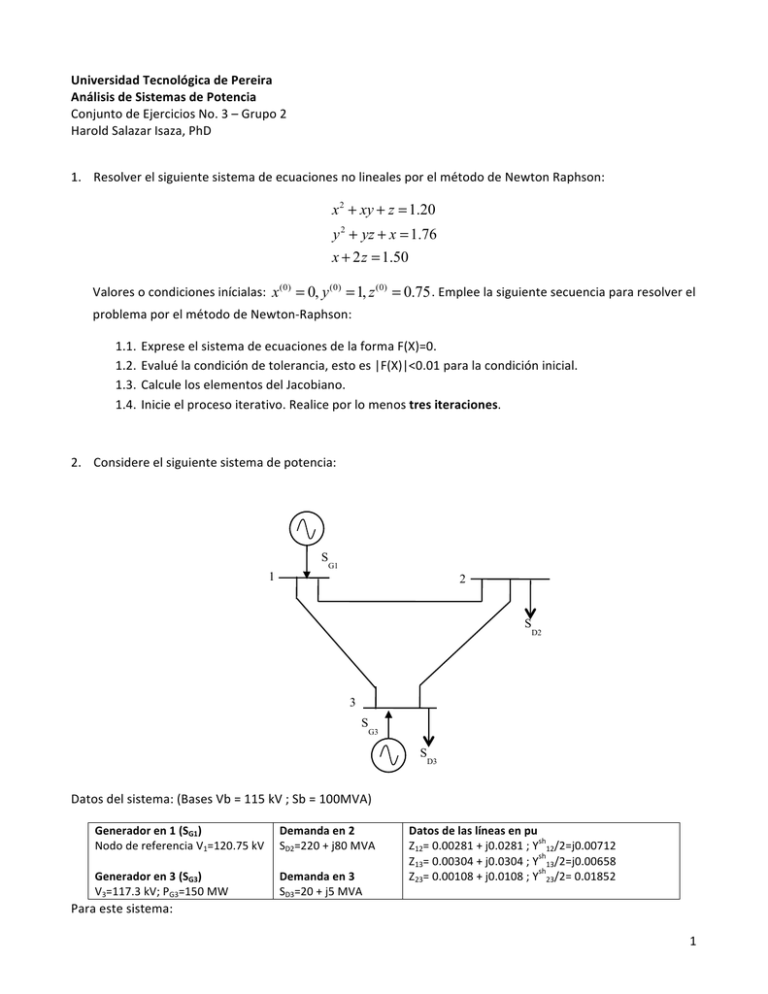
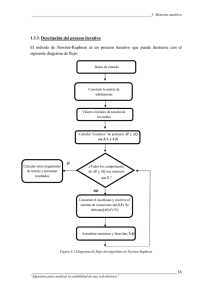
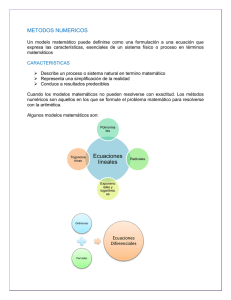
UniversidadTecnológicadePereira
AnálisisdeSistemasdePotencia
ConjuntodeEjerciciosNo.3–Grupo2
HaroldSalazarIsaza,PhD
1. ResolverelsiguientesistemadeecuacionesnolinealesporelmétododeNewtonRaphson:
x 2 + xy + z = 1.20
y 2 + yz + x = 1.76 x + 2 z = 1.50
Valoresocondicionesinícialas: x(0) = 0, y (0) = 1, z (0) = 0.75 .Empleelasiguientesecuenciapararesolverel
problemaporelmétododeNewton-Raphson:
1.1. ExpreseelsistemadeecuacionesdelaformaF(X)=0.
1.2. Evaluélacondicióndetolerancia,estoes|F(X)|<0.01paralacondicióninicial.
1.3. CalculeloselementosdelJacobiano.
1.4. Inicieelprocesoiterativo.Realiceporlomenostresiteraciones.
2. Considereelsiguientesistemadepotencia:
S
1
G1
2
S
D2
3
S
G3
S
D3
Datosdelsistema:(BasesVb=115kV;Sb=100MVA)
Generadoren1(SG1)
NododereferenciaV1=120.75kV
Generadoren3(SG3)
V3=117.3kV;PG3=150MW
Demandaen2
SD2=220+j80MVA
Demandaen3
SD3=20+j5MVA
Datosdelaslíneasenpu
sh
Z12=0.00281+j0.0281;Y 12/2=j0.00712
sh
Z13=0.00304+j0.0304;Y 13/2=j0.00658
sh
Z23=0.00108+j0.0108;Y 23/2=0.01852
Paraestesistema:
1
2.1. ResolverelflujodepotenciaporelmétodoDC.
2.2. ResolverelflujodepotenciaporelmétodoNewton-Raphsoniniciandoconvoltajesplanos.Considere
unatoleranciade1MVA.ConlasrespuestasdelmétododeNewton-Raphsoncontestelassiguientes
preguntas:
a) Determineelflujodepotenciaactivayreactivaquesaledelasubestación2alasubestación3.
b) Determineelflujodepotenciaactivayreactivaquesaledelasubestación3alasubestación2.
c) Expliquelarazónporlacuallasrespuestasalasdospreguntasanterioressondiferentes.
d) Calculeyexpliqueelsignodelapotenciareactivadelgeneradorconectadoenlasubestación3.
2.3. ResolverelflujodepotenciaporelmétodoNewton-Raphsoniniciandoconelresultadosdelflujode
potenciaDC.Considereunatoleranciade1MVA.
2.4. Resolver el flujo de potencia por el método Newton-Raphson desacoplado iniciando con voltajes
planos.Considereunatoleranciade1MVA.
2.5. Resolver el flujo de potencia por el método Newton-Raphson desacoplado rápido iniciando con
voltajesplanos.Considereunatoleranciade1MVA.
2.6. Asuma que el generador de la subestación 3 disminuye su voltaje a 104kV. Resuelva el flujo de
potenciaporelmétodoNewton-Raphsondesacopladoconsiderandoqueelvoltajeenlasubestación
2debeestarentre0.95y1.05pu.Ignoreloslímitesdepotenciareactivadelgenerador3yconsidere
unatoleranciade1MVA.InicieconelresultadodeunflujodepotenciaDC.
2.7. Asumaqueelgeneradordelasubestación3aumentasuvoltajea115kV.Resuelvaelflujodepotencia
por el método Newton-Raphson considerando que el límite inferior de potencia reactiva del
generador3es200MVAr.Ignoreloslímitesdevoltajesdelassubestacionesyconsidereunatolerancia
de1MVA.InicieconelresultadodeunflujodepotenciaDC.
Recuerdelasiguientesecuenciapararesolverunejerciciodeflujodepotencia:
a) Representeelsistemaenporunidad(p.u).
b) EstablezcalamatrizYbus.
RECUERDEQUELOSSIGUIENTESTRESPUNTOSSEPUEDENREALIZARENUNATABLA
c) Clasifiquetodoslosnodos(subestaciones)delsistema.
d) Establezca las variables nodales conocidas y desconocidas para cada nodo según la
clasificacióndelpuntoanterior.
e) Determineelconjuntodeecuacionesútilessegúnlaclasificacióndelosnodos.
f) EstablezcalostérminosdelJacobianoSEGÚNelmétodorequerido.
g) InicieelprocesoiterativoSEGÚNelmétodorequerido.
3. Para el ejercicio anterior, considere que existe un transformador con cambiador de toma (tap) entre las
subestaciones 1 y 2. Determine el valor del tap para sostener el voltaje en la subestación 2 en 0.99pu
empleando el método de Newton-Raphson. Considere que el transformador tiene una reactancia de
j0.05pu.Utilicelaactualizaciónautomáticadeltapdentrodelprocesoiterativo.
2
4. ResolverlossiguientesejerciciosdellibroAnálisisdeSistemasdePotencia–JohnJ.GraingeryWilliamD.
Stevenson,edición1996enespañol.
4.1.
4.2.
4.3.
4.4.
4.5.
Ejercicio9.14porelmétododeNewton-Raphson
Ejercicio9.15
Ejercicio9.18
Ejercicio9.19
Ejercicio9.20
3