Problemas 2 y 3
Anuncio

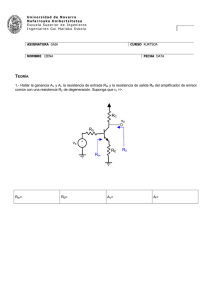
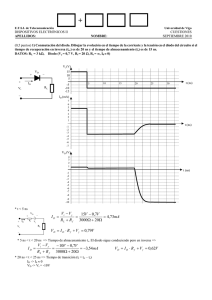
Dispositivos Electrónicos II. E.T.S.I. Telecomunicaciones de Vigo. Diciembre 2009. Problema 3. Dado el siguiente amplificador basado en un transistor FET calcular: a) Su ganancia de tensión a frecuencias medias. b) La repuesta en baja frecuencia. c) La respuesta en alta frecuencia. d) Dibujar el diagrama de bode. Datos: gm= 0.0102 S, CGS= 11.8 pF, CGD= 5.42 pF. Como el polo introducido por CS es el de mayor frecuencia es el que fija la frecuencia de corte inferior, es decir, fL= 987 Hz. Sin embargo, como el cero está a una frecuencia de 249 Hz, que no está muy lejos de 987, esta solución es aproximada. Como se comprueba en la gráfica del resultado de la simulación, la frecuencia exacta sería 912 Hz, que es ligeramente inferior. Para obtener la respuesta en frecuencia a bajas frecuencias, se puede partir de la siguiente figura. RD 2.2 kΩ ZG Rin Vout Rin Vin CG VCC Q1 600 Ω D G vgs RG 2.2 µF g m ⋅ v gs - RG 470 kΩ RS 290 Ω CS 2.2 µF Vo + + vin 12 V CG ZS RD S RS CS Figura 1.1. Circuito amplificador basado en FET en surtidor común. a) A frecuencias medias se cortocircuitan los condensadores CG y CS. Las capacidades parásitas del transistor no se tienen en cuenta. El circuito equivalente de pequeña señal para frecuencias medias es el siguiente: Rin vin G D Vo + + RG vgs g m ⋅ v gs - RD S Figura 1.2. Circuito equivalente a frecuencias medias. v gs = vg = vin ⋅ RG RG + Rin vo = − g m ⋅ v gs ⋅ RD Avm = vo − g m ⋅ v gs ⋅ RD RG = = − g m ⋅ RD ⋅ = RG + Rin vin RG + Rin v gs ⋅ RG = −0.010 2 ⋅ 2 200 ⋅ 1 = 0.153 Hz 2 ⋅ π ⋅ 2.2 ⋅10 −6 ⋅ 470 600 1 1 = = 249.5 Hz f zCS = 2 ⋅ π ⋅ C S ⋅ RS 2 ⋅ π ⋅ 2.2 ⋅10 −6 ⋅ 290 (1.2) v in = v gs ⋅ (1 + g m ⋅ Z S )⋅ (1.3) g m ⋅ RS + 1 0.0102 ⋅ 290 + 1 = = 987.36 Hz 2 ⋅ π ⋅ C S ⋅ RS 2 ⋅ π ⋅ 2.2 ⋅ 10 −6 ⋅ 290 Camilo Quintáns Graña y Miguel Ángel Domínguez Gómez. Av = =− Z in = (1.7) − − g m ⋅ v gs ⋅ RD = R + Z in v gs ⋅ (1 + g m ⋅ Z S ) ⋅ G RG (1.11) (1.12) RS 1 // RS = CS ⋅ s 1 + RS ⋅ C S ⋅ s (1.13) 1 + Rin ⋅ CG ⋅ s CG ⋅ s (1.14) 1 CG ⋅ s Av = − =− (1.6) vo = vin RG + Z in RG (1.10) g m ⋅ RD RG ⋅ 1 + g m ⋅ Z S RG + Z in ZS = (1.5) = f pCS = RG − g m ⋅ v gs ⋅ Z S RG + Z in v gs =v g −v S = vin ⋅ (1.4) Que en decibelios es: Avm = 20 ⋅ log − 22.41 = 27 dB b) Para calcular la respuesta en baja frecuencia no se tienen en cuenta las capacidades parásitas del transistor, de forma que la respuesta a bajas frecuencias viene dada por los condensadores CG y CS. CG introduce un cero en el origen y un polo dado por (1.5). CS introduce un cero en (1.6) y un polo en (1.7). f pCG Las tensiones en el surtidor y en la puerta vienen dados, respectivamente, por (1.8) y (1.9). Por tanto, la tensión puertasurtidor se corresponde con (1.10), de la que se puede despejar la tensión de entrada. A continuación se sustituye en la expresión de la ganancia (1.12), en la que, además, también se sustituyen las expresiones (1.13) y (1.14) de las impedancias de entrada y de surtidor. Finalmente se obtiene la expresión general para bajas frecuencias (1.15). (1.9) v S = g m ⋅ v gs ⋅ Z S (1.8) ; v g = vin ⋅ RG RG + Z in (1.1) 470 000 = −22.41 470 600 1 = = 2 ⋅ π ⋅ C G ⋅ (Rin + RG ) Figura 1.3. Circuito equivalente a baja frecuencia + Rin = RG g m ⋅ RD = ⋅ 1 + Rin ⋅ CG ⋅ s RS 1 + gm ⋅ RG + 1 + RS ⋅ C S ⋅ s CG ⋅ s g m ⋅ RD ⋅ (1 + RS ⋅ C S ⋅ s ) RG ⋅ CG ⋅ s = ⋅ 1 + RS ⋅ C S ⋅ s + g m ⋅ RS RG ⋅ CG ⋅ s + 1 + Rin ⋅ CG ⋅ s (1.15) 1 + RS ⋅ C S ⋅ s g m ⋅ RD ⋅ RG ⋅ CG s ⋅ = ⋅ RS ⋅ C S ( 1 + g m ⋅ RS RG + Rin ) ⋅ CG ⋅ s + 1 ⋅ s +1 1 + g m ⋅ RS = −5.86 ⋅ 1 + 6.038 ⋅ 10 −4 ⋅ s s ⋅ 1.6119 ⋅ 10 −4 ⋅ s + 1 1.035 ⋅ s + 1 1 Dispositivos Electrónicos II. E.T.S.I. Telecomunicaciones de Vigo. Diciembre 2009. k p = 20 ⋅ log − 5.86 = 15.36 dB (1.16) c) Para calcular la respuesta en alta frecuencia se consideran cortocircuitos los capacitares CS y CG y se añaden las capacidades parásitas del transistor, pasando la capacidad puerta-drenador a la entrada y la salida aplicando el teorema de Miller. Los polos que aparecen a altas frecuencias son: 1 = 1.9 MHz 2 ⋅ π ⋅ (Rin // RG ) ⋅ C gs + C gd ⋅ (1 − ( − g m ⋅ RD ) ) f p1 = [ f p2 = ] 1 ⎡ 2 ⋅ π ⋅ RD ⋅ ⎢C gd ⎣ Rin G ⎛ ⎞⎤ 1 ⎟⎥ ⋅ ⎜⎜1 − − g m ⋅ RD ⎟⎠ ⎦ ⎝ RE3 360 Ω RC2 6043 Ω 12 + Q3 Q1 Vo 1⎞ ⎛ C gd ⋅ ⎜1 − ⎟ K ⎝ ⎠ g m ⋅ v gs RG VCC = 12.78 MHz D + vin Problema 2. Dado el siguiente circuito, calcular: a) La ganancia de pequeña señal de tensión diferencial, Av= Vo/Vd. b) La capacidad de un condensador Cbc tal que, si se añade al circuito conectado entre los terminales de base y colector de Q3, haga que la frecuencia de corte superior del amplificador sea de 200 Hz. Datos:VBEQ(Q1, Q2)=0.76 V, hfe= 100, VT=25.8 mV, VoQ= 0 V. Q2 + Vd/2 RD Vo Vd/2 + 12 RC3 2 kΩ REE 10 kΩ + VEE S C gs + C gd ⋅ [1 − K ] Figura 1.4. Circuito equivalente de pequeña señal a altas frecuencias. a) Resultado de la simulación: I E2 = R1 2.2k 1Vac 0Vdc R5 C1 600 2.2u V1 Jbreakn J1 12Vdc V2 R2 470k R4 290 (2.1) 1 12 V − 0.76 V = ⋅ = 562 µA 2 10 kΩ β 100 IC2 = I E2 ⋅ = 562 µA ⋅ = 556.4 µA β +1 101 Vout Vin 1 1 VEE − VBEQ 2 ⋅ I EE = ⋅ = 2 2 REE I C3 = C2 2.2u 0 (2.2) Vo − VEE 0 V − (−12 V ) = = 6 mA RC 3 2 kΩ Vd − ib1 ⋅ hie1 2 (2.3) Vd − ib 2 ⋅ hie 2 2 (2.4) ; (2.5) Sumando (2.4) y (2.5), y considerando que las resistencias de entrada de Q1 y Q2 son iguales, se obtiene (2.6): Vp = − Figura 1.5. Esquema del circuito de OrCAD. Vp = 2 ⋅ V p = −(ib1 + ib 2 ) ⋅ hie (ib1 + ib 2 ) ⋅ (1 + h fe ) = Figura 1.6. Modelo del transistor. DB(V(Vout) / V(Vin)) 30 (1.69 MHz, 23.98 dB) (912 Hz, 23.94 dB) (26.98 dB) 20 (153 mHz, 12.02 dB) (15.05 dB) 100 Hz 10 kHz 1.0 MHz 50 MHz Frecuencia [Hz] Figura 1.7. Respuesta en frecuencia resultado de la simulación con PSpice. Parámetros del transistor en el punto de polarización: NAME J_J1 MODEL Jbreakn ID 2.88E-03 VGS -8.35E-01 VDS 4.83E+00 GM 1.02E-02 GDS 0.00E+00 CGD 5.42E-12 CGS 1.18E-11 Camilo Quintáns Graña y Miguel Ángel Domínguez Gómez. (ib1 + ib 2 ) = Vp REE ⋅ (1 + h fe ) (2.8) Ahora, sustituyendo (2.8) en (2.6), se obtiene la expresión (2.9), que sólo puede ser cierta si la tensión Vp es nula. Vp (2.9) 2 ⋅ Vp = − ⋅ hie REE ⋅ (1 + h fe ) ib 2 = 1.0 Hz V p (2.7); REE Como Vp=0 V, entonces: (266.92 dB, 18.06 dB) 10 0 10 mHz (2.6) Vd 2 ⋅ hie 2 (2.10) Vd ic 2 = ib 2 ⋅ h fe = ⋅ h fe 2 ⋅ hie 2 vb 3 = −ic 2 ⋅ (RC 2 // Req 3 ) = (2.11) (11) [ ] R ⋅ h + RE 3 ⋅ (1 + h fe ) V = − d ⋅ h fe ⋅ C 2 ie 3 2 ⋅ hie 2 RC 2 + hie3 + RE 3 ⋅ (1 + h fe ) hie 2 = h fe ⋅ VT 100 ⋅ 25.8 = = 4 607 Ω I C 2Q 0.56 (2.12) (2.13) 2 Dispositivos Electrónicos II. E.T.S.I. Telecomunicaciones de Vigo. Diciembre 2009. hie 3 = h fe ⋅ VT I C 3Q = 100 ⋅ 25.8 = 430 Ω 6 (2.14) V Av1 = b 3 = Vd (2.15) 100 6 043 ⋅ [430 + (360 ⋅ 101)] =− ⋅ = −56.3 2 ⋅ 4 607 6 043 + 430 + (360 ⋅ 101) Av 2 = = − RC 3 ⋅ h fe ⋅ ib 3 Vo = = Vb 3 ib3 ⋅ hie 3 + ib3 ⋅ (h fe + 1)⋅ RE 3 − 2 000 ⋅100 = −5.44 430 + 101 ⋅ 360 (2.16) V V V Av = o = b 3 ⋅ o = Vd Vd Vb 3 = Av1 ⋅ Av 2 = (− 56.3)⋅ (− 5.44 ) = 306.27 (2.17) c) El condensador Cbc tendrá su mayor efecto en la entrada, por el teorema de Miller. Por lo que queda en paralelo con RC2 y la resistencia que ve es R3=RC2//Req3. Además, la ganancia de Miller es Av2= -5.44, por tanto: 1 (2.18) Cbc ⋅ (1 − Av 2 ) = 2 ⋅ π ⋅ R3 ⋅ f H Cbc = 1 [1 − (− 5.44)]⋅ 2 ⋅ π ⋅ 5 190.436 ⋅ 200 = 23.8 nF (2.19) PARAMETERS: RE = 1000 VCC R1 359 R2 6043 V1 12 Qbreakp 9.000V Q2 V2 C1 Q3 QbreakN V1 1Vac 0Vdc 12.00V Vo 23.8nF QbreakN R4 10k Q1 0 R3 2k V4 V3 12 0V -759.0mV VEE 0 50 (198 Hz, 46.5 dB) 25 0 1.0Hz 100Hz DB(V(Vo)/( V(V1) - V(V2))) Frequency 10KHz Camilo Quintáns Graña y Miguel Ángel Domínguez Gómez. 1.0MHz 3