Práctica 1: Métodos clásicos de análisis de series temporales

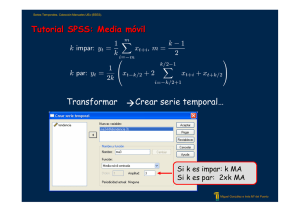
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos clásicos de análisis de
series temporales
Objetivos:
• Comprender e interpretar las fuentes de variación de
una serie temporal.
• Comprender y saber aplicar los métodos clásicos y el
método STL para la descomposición de una serie
temporal.
• Comprender y saber aplicar los métodos de suavizado
exponencial para saber describir y realizar predicciones
de una serie temporal.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos clásicos de análisis de
series temporales
Representación gráfica:
Componente
ComponenteEstacional
Estacional
Cambio
CambioCíclico
Cíclico
Tendencia
Tendencia
Tendencia-Ciclo
Componente
Componenteirregular
irregular
Métodos de descomposición
Métodos clásicos
Métodos de suavizado
exponencial
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Objetivo: Identificar y aislar, de la forma más precisa posible,
cada una de las componentes de variación presentes en la serie.
Xt = f(Tt , St , It )
XXt Dato
en el instante t
t Dato en el instante t
Tendencia-Ciclo en el instante t
TTt Componente
t Componente Tendencia-Ciclo en el instante t
Estacional en el instante t
SSt Componente
t Componente Estacional en el instante t
Irregular en el instante t
IIt Componente
t Componente Irregular en el instante t
log
Modelo aditivo: Xt = Tt + St + It
Modelo multiplicativo: Xt = Tt · St · It
Modelo mixto: Xt = Tt + St · It
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Ejercicio: Utiliza el software estadístico y lenguaje de
programación R para simular series temporales donde las
componentes de variación actúen de manera aditiva y/o
multiplicativa.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Descomposición clásica: SPSS
Aditiva y multiplicativa
Menú: Analizar Æ Series temporales Æ Descomposición
estacional… Tutorial SPSS
Descomposición clásica: R
decompose()
Aditiva y mixta
Herramienta Principal: Media Móvil
m
X
1
k−1
k impar: yt =
xt+i , m =
k i=−m
2
⎞
⎛
k/2−1
X
1 ⎝
k par: yt =
xt+i + xt+k/2 ⎠
xt−k/2 + 2
2k
i=−k/2+1
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Descomposición clásica: SPSS
Modelo aditivo: Xt=Tt+St+It
•
•
•
•
•
•
Tt’ = 2xs MA(Xt)
Rt=Xt-Tt’
St
Xt-St=Tt+It
Tt= 3x3 MA(Xt-St)
It=Xt-St-Tt
Moving averages
Ratios
Seasonal factors
Seasonally adjusted series
Smoothed trend-cicle
Irregular component
s = periodo de la componente estacional. P.e.: s=4, datos
trimestrales; s=12, datos mensuales, etc.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Descomposición clásica: SPSS
Modelo multiplicativo: Xt=Tt● St● It
•
•
•
•
•
•
Tt’ = 2xs MA
Rt=Xt/Tt’ ● 100
St
Xt/St=Tt● It
Tt= 3x3 MA(Xt/St)
It=Xt/(St● Tt)
Moving averages
Ratios (● 100)
Seasonal factors
Seasonally adjusted series
Smoothed trend-cicle
Irregular component
s = periodo de la componente estacional. P.e.: s=4, datos
trimestrales; s=12, datos mensuales, etc.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Descomposición STL: R
“A seasonal-trend decomposition procedure based on Loess''
Cleveland, R.B., Cleveland, W.S., McRae, J.E. & Terpenning, I.
(1990). Stl: A seasonal-trend decomposition procedure based on loess (with
discussion). Journal of Official Statistics, 6, 3-73.
Herramienta Principal:
Suavizado de Loess:
Cleveland, W. & Devlin, S. (1988). Locally weighted regression: an aproach
to regression analysis by local fitting. Journal of America Statistical Association, 74, 596-610.
Cleveland, W., Devlin, S. & Grosse, E. (1988). Regression by local
fitting: methods, properties and computational algorithms. Journal of Econometrics, 37, 87-114.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Locally Weighted Regression Smoothing (Loess-Smooth)
Se construye una función suavizada del siguiente modo:
1. Tomamos un punto, x0 . Encontramos los k valores más cercanos a x0 , que
constituyen el conjunto N (x0 ). El número de valores cercanos, k, se especifica como una proporción del número total de puntos. Esta proporción se
denomina span y por defecto toma el valor 2/3.
2. Calculamos la mayor distancia entre x0 y cualquier otro punto de N (x0 ):
∆(x0 ) = maxxi ∈N (x0 ) |x0 − xi |.
3. Asignamos³ pesos a´ cada punto de N (x0 ) utilizando la función de peso triple
cubo: W
|x0 −xi |
∆(x0 )
donde W (u) = (1 − u3 )3 si 0 ≤ u < 1; 0 en otro caso.
4. Calculamos el ajuste de mı́nimos cuadrados ponderados de y sobre N (x0 ).
Se toma el valor ajustado ŷ0 = S(x0 ).
5. Repetimos el proceso para cada valor de la variable predictora.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Funciones en R
Suavizado de Loess: loess.smooth()
Descomposición STL: stl()
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
Ejercicios:
1) Estima la tendencia de la serie almacenada en el archivo tendencia
utilizando los métodos de suavizado de medias móviles y de Loess.
2) Estima con el método que creas más adecuado la tendencia de la serie
precio medio del metro cuadrado de vivienda libre en España descrita
en el ejemplo 1.3 del Manual.
3) En el archivo casas se encuentran almacenados los datos de las ventas
mensuales (en miles) de casas unifamiliares de nueva construcción
vendidas en EEUU desde enero de 1973 a noviembre de 1995.
a) Representa la serie e identifica las componentes de variación
presentes en la misma.
b) Estima la tendencia y los índices estacionales haciendo uso de un
método de descomposición clásico.
c) Repite b) con el método de descomposición STL.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
4) En el archivo pasajeros se encuentran datos mensuales
correspondientes al número total de pasajeros (en miles) de las
compañías de aerolíneas internacionales, desde enero de 1949 hasta
diciembre de 1960.
a) Representa la serie e identifica las componentes de variación
presentes en la misma.
b) Utiliza los métodos de descomposición clásicos y STL para
estimar la tendencia y calcular los índices estacionales y valora qué
metodología es la más adecuada.
5) En el archivo ordenadores se encuentran almacenados los datos
correspondientes a las ventas mensuales de ordenadores durante un
periodo de 5 años.
a) Representa la serie e identifica las componentes de variación
presentes en la misma.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de descomposición
b) Utiliza los métodos de descomposición clásicos y STL para
estimar la tendencia y calcular los índices estacionales. Valora qué
metodología es la más adecuada.
c) Comenta si los resultados obtenidos en b) están de acuerdo con la
interpretación gráfica del apartado a).
6) Determina el método de descomposición más apropiado para estimar
la componente de tendencia y los índices estacionales de la serie
horas semanales trabajadas por ocupado en España descrita en el
ejemplo 1.6 del Manual.
7) Utiliza el método de descomposición más adecuado para estimar las
componentes de variación de la serie ingresos y pagos por turismo
descrita en el ejemplo 1.8 del Manual.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Objetivo: Eliminar las fluctuaciones aleatorias y tratar de
aprovechar cualquier conducta evidente con la finalidad de
predecir nuevos valores.
¿Cómo predicen? Los predicciones que proponen los
métodos de suavizado exponencial son medias de valores
pasados, aplicando un conjunto desigual de pesos a los
datos. Su nombre se debe a que los pesos decaen,
generalmente, de una forma exponencial desde el dato más
reciente al más distante.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Suavizado
Suavizado exponencial
exponencial simple:
simple: Series
Series sin
sin tendencia
tendencia yy
sin
sin componente
componente estacional
estacional
x̂t+1 = αxt + (1 − α)x̂t
x̂t+1 = αxt + α(1 − α)xt−1 + . . . + α(1 − α)t−1 x1 + (1 − α)t x̂1
α ∈ [0, 1]
x̂1
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Suavizado
Suavizado exponencial
exponencial de
de Holt:
Holt: Series
Series con
con tendencia
tendencia
lineal
lineal yy sin
sin componente
componente estacional
estacional
Nivel : Lt
Tendencia : bt
Predicción : x̂t+m
= αxt + (1 − α)(Lt−1 + bt−1 )
= β(Lt − Lt−1 ) + (1 − β)bt−1
= Lt + bt m
α, β ∈ [0, 1]
L 1 , b1
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Suavizado
Suavizado exponencial
exponencial de
de Holt-Winters:
Holt-Winters: Series
Series con
con
tendencia
tendencia yy componente
componente estacional
estacional
Modelo multiplicativo
Nivel : Lt
=
Tendencia : bt
=
Componente Estacional: St
=
Predicción: x̂t+m
=
xt
α
+ (1 − α)(Lt−1 + bt−1 )
St−s
β(Lt − Lt−1 ) + (1 − β)bt−1
xt
γ
+ (1 − γ)St−s
Lt
(Lt + bt m)St−s+m
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Suavizado
Suavizado exponencial
exponencial de
de Holt-Winters:
Holt-Winters: Series
Series con
con
tendencia
tendencia yy componente
componente estacional
estacional
Modelo aditivo
Nivel : Lt
Tendencia : bt
Componente Estacional: St
Predicción: x̂t+m
=
=
=
=
α(xt − St−s ) + (1 − α)(Lt−1 + bt−1 )
β(Lt − Lt−1 ) + (1 − β)bt−1
γ(xt − Lt ) + (1 − γ)St−s
(Lt + bt m) + St−s+m
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Clasificación de Pegel (1969)
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Suavizado Exponencial: SPSS
Tutorial SPSS
Menú: Analizar Æ Series temporales Æ Suavizado exponencial…
Suavizado Exponencial: R
HoltWinters()
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
Ejercicios:
1) En el archivo cantidad se encuentran almacenados los datos
correspondientes a los totales diarios de inventarios de unidades de
alimentación utilizados en impresoras (149 observaciones).
a) Analiza las componentes de variación presentes en la serie,
realizando un gráfico de secuencia.
b) Estima modelos de suavizado exponencial simple y lineal de Holt para
estos datos, utilizando como conjunto de inicio desde la observación 1 a
la 100.
c) Compara los errores cuadráticos medios sobre el conjunto de
prueba de la observación 101 a la 149 correspondientes a los modelos
estimados en b).
d) A partir de c), determina qué método es más adecuado para hacer
predicciones y pronostica 3 valores futuros de las serie.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
2) Utiliza el software estadístico y lenguaje de programación R
para generar a partir de la serie población mayores de 16 años
en España, descrita en el ejemplo 1.2 del Manual, una serie
temporal con una presencia más acusada de la componente
irregular. Propón un método de predicción para la serie obtenida.
3) Determina qué método de suavizado exponencial es más
adecuado para realizar predicciones para la serie almacenada en
el archivo ventas correspondiente a las exportaciones
trimestrales de una compañía francesa durante un periodo de 6
años, valorando los errores cuadráticos medios sobre el conjunto
de prueba que contiene los datos correspondientes a los dos
últimos años.
Miguel González e Inés Mª del Puerto
Series Temporales. Colección Manuales UEx (EEES).
Práctica 1: Métodos de suavizado exponencial
4) Determina qué método de suavizado exponencial es más
adecuado para realizar predicciones para cada uno de los
siguientes conjuntos de datos:
a) Variaciones mensuales del IPC nacional relativo a alimentos y
bebidas no alcohólicas, descrita en el ejemplo 1.1 del Manual.
b) Horas semanales trabajadas por ocupado en España, descrita
en el ejemplo 1.6 del Manual.
c) Ingresos y pagos por turismo en España, descrita en el
ejemplo 1.8 del Manual.
d) Número total mensual de pasajeros (en miles) de las
compañías de aerolíneas internacionales, descrita en el problema
1.5 del Manual.
5) Establece una ecuación de predicción para la serie total de
acciones en el mercado bursátil español, descrita en el ejemplo
1.7 del Manual.
Miguel González e Inés Mª del Puerto