Ejercicios punto, recta y plano

CURSO 0 2013-2014 – Representación del Punto, la Recta y el Plano en sistema diédrico [ejercicios]
Ejercicios propuestos días 02/09/2013 y 03/09/2013
1. Representa un punto en sistema diédrico sabiendo que está:
-
… por encima del primer y del segundo plano bisector y por delante del PVP.
-
… detrás del PVP y encima del segundo bisector.
-
… en el segundo bisector y con cota negativa.
-
… con coordenadas A (0,-1,-1).
-
… en una recta vertical que pasa por B (1,1,1) [descartando B].
-
… en una recta horizontal que pasa por C (0,1,1) [descartando C].
-
... en un plano proyectante horizontal que contiene a D (0,2,2) [descartando D].
-
… en una recta que pasa por O (0,0,0) y E (2,2,2) [descartando O y E].
-
… en la intersección de la recta R {A (0,1,2), B (2,0,5)} con el PVP.
-
… en la intersección de la recta R con el PHP.
-
… en la intersección de la recta R con el primer bisector y en el primer cuadrante.
-
… en la intersección de una recta vertical que pasa por el punto F (0,2,2) y el segundo
bisector.
2. Obtén la distancia, en verdadera magnitud, que hay entre el punto G (1,1,1) y H (3,1,6)
3. Obtén la distancia, en verdadera magnitud, que hay entre el punto I (1,1,1) y J (3,6,1)
4. Representa, con partes vistas y ocultas, la recta T {A(-2,3,1), B(2,1,3)}
5. Obtén una recta que pertenezca al plano P (-3,3,4)
6. Obtén un punto que pertenezca al plano Q (3,4,3)
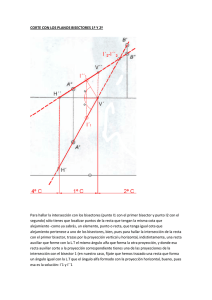
7. Obtén la línea de máxima pendiente y de máxima inclinación del plano H (-3,4,3)
8. Obtén las trazas de dos rectas que se corten y que pertenezcan al plano I (-3,4,4)
9. Obtén las coordenadas de un punto cualquiera de cada una de las rectas del ejercicio
anterior así como las coordenadas del punto de intersección
10. Completa y resuelve el siguiente enunciado:
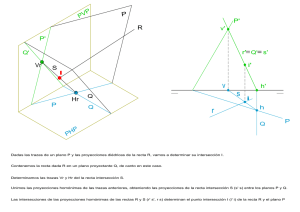
Dadas dos rectas R{A( , , ), E( , , )} y T{B( , , ), E( , , )} obtén las trazas del plano que determinan
11. Dibuja dos rectas paralelas
12. Dibuja dos rectas perpendiculares
[Notas: en cada ejercicio el origen de coordenadas está centrado y las cotas están dadas en
centímetros, en el caso de existir múltiples soluciones se elegirá una cualquiera]
Pablo Jeremías Juan Gutiérrez (pablo.juan@ua.es)
UNIVERSIDAD DE ALICANTE